2022.7.26学习笔记

主要内容：

1.堆
2.并查集
3.线段树
4.可持久化线段树
5.树状数组

堆

定义：

　　堆(heaps)不是容器，而是一种特别的数据组织方式。堆一般用来保存序列容器。

　　1.堆是一棵完全二叉树
　　2.不仅仅是完全二叉树

种类：

1.大根堆:
　　每个结点的权值都比儿子的权值大
2.小根堆:
　　每个结点的权值都比儿子的权值小
3.因为堆的性质，大根堆的根结点一定权值最大，小根堆的根结点一定权值最
小

优先队列：

优先队列定义： priority_queue<Type, Container, Functional>
tips：Type 就是数据类型，Container 就是容器类型（Container必须是用数组实现的容器，比如vector,deque等等，
但不能用 list。STL里面默认用的是vector），Functional 就是比较函数，当需要用自定义的数据类型时才需要
传入这三个参数，使用基本数据类型时，只需要传入数据类型，默认是大顶堆。
　　priority_queue <int, vector<int>, greater<int> > q; //升序队列
　　priority_queue <int, vector<int>, less<int> >q; //降序队列
头文件：
#include <queue>
基本操作：
empty() 如果队列为空，则返回真
pop() 删除对头元素，删除第一个元素
push() 加入一个元素
size() 返回优先队列中拥有的元素个数
top() 返回优先队列对头元素，即优先级最高的元素
　　在默认的优先队列中，优先级高的先出队。在默认的int型中先出队的为较大的数。

结构体创建优先队列：

#include<bits/stdc++.h>
#include<queue>
using namespace std;
const int maxn=10010;
struct node {
    int v;
    bool operator<(const struct node x)const {
        return v>x.v;
    }
}cur;
priority_queue<struct node> pq;
int main() {
    int n,sum=0;
    scanf("%d",&n);
    for(int i=0; i<n; i++) {
        scanf("%d",&cur.v);
        pq.push(cur);
    }
    for(int i=1; i<n; i++) {
        cur=pq.top();
        pq.pop();
        cur.v+=pq.top().v;
        pq.pop();
        sum+=cur.v;
        pq.push(cur);
    }
    printf("%d\n",sum);
    return 0;
}

堆排序：

即利用堆的特性进行排序的一种排序方法。
1. 建立初始大顶堆，即将整个序列调整为堆
2. 输出根结点，将堆顶元素和最后元素交换，从堆中删除原来的堆顶元素
3. 重新调整为大顶堆
4.重复第2、3步，直到所有的元素都被删除。

堆排序模板：

#include<bits/stdc++.h> 
using namespace std;
const int N = 100010;
int n, m;
int h[N], cnt;
void down(int u) {
    int t = u;
    if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if (u != t) {
        swap(h[u], h[t]);
        down(t);
    }
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
    cnt = n;
    for (int i = n / 2; i; i -- ) down(i);
    while (m -- ) {
        printf("%d ", h[1]);
        h[1] = h[cnt -- ];
        down(1);
    }
    puts("");
    return 0;
}

并查集

定义：

并查集是一种多叉树，用于处理一些不相交集合的合并及查询问题。

1.初始化：每个结点单独作为一个集合。

2.查询：求元素所在的集合的代表元素，即根结点。

3.合并：将两个元素所在的集合，合并为一个集合。

例题：

P2024 [NOI2001] 食物链

题目描述

动物王国中有三类动物 A,B,C，这三类动物的食物链构成了有趣的环形。A 吃 B，B 吃 C，C 吃 A。

现有 N 个动物，以 1 － N 编号。每个动物都是 A,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 N 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 X 和 Y 是同类。
第二种说法是2 X Y，表示 X 吃 Y 。

此人对 N 个动物，用上述两种说法，一句接一句地说出 K 句话，这 K 句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话
当前的话中 X 或 Y 比 N 大，就是假话
当前的话表示 X 吃 X，就是假话

你的任务是根据给定的 N 和 K 句话，输出假话的总数。

输入格式

第一行两个整数，N，K，表示有 N 个动物，K 句话。

第二行开始每行一句话（按照题目要求，见样例）

输出格式

一行，一个整数，表示假话的总数。

输入输出样例

输入 #1

输出 #1

说明/提示

1 ≤ N ≤ 5 ∗ 10^4

1 ≤ K ≤ 10^5

#include<bits/stdc++.h>
using namespace std;
const int N=50010;
struct node {
    int pre;
    int relation;
} p[N];
int find(int x) {
    int temp;
    if(x == p[x].pre)
        return x;
    temp = p[x].pre;
    p[x].pre = find(temp);
    p[x].relation = (p[x].relation + p[temp].relation)%3;
    return p[x].pre;
}
int main() {
    int n,k;
    int ope,a,b;
    int root1,root2;
    int sum=0;
    scanf("%d%d",&n,&k);
    for(int i=1; i<=n; ++i) {
        p[i].pre=i;
        p[i].relation = 0;
    }
    for(int i = 1; i <= k; ++i) {
        scanf("%d%d%d", &ope, &a, &b);
        if(a>n|| b>n) {
            sum++;
            continue;
        }
        if(ope == 2 && a == b) {
            sum++;
            continue;
        }
        root1 = find(a);
        root2 = find(b);
        if(root1 != root2) {
            p[root2].pre = root1;
            p[root2].relation = (3 + (ope - 1) +p[a].relation - p[b].relation) % 3;
        } else {
            if(ope == 1 && p[a].relation != p[b].relation) {
                sum++;
                continue;
            }
            if(ope == 2 && ((3 + p[b].relation - p[a].relation) % 3 != ope - 1)) {
                sum++;
                continue;
            }
        }
    }
    printf("%d\n", sum);
    return 0;
}#include<bits/stdc++.h>
using namespace std;
const int N=50010;
struct node {
    int pre;
    int relation;
} p[N];
int find(int x) {
    int temp;
    if(x == p[x].pre)
        return x;
    temp = p[x].pre;
    p[x].pre = find(temp);
    p[x].relation = (p[x].relation + p[temp].relation)%3;
    return p[x].pre;
}
int main() {
    int n,k;
    int ope,a,b;
    int root1,root2;
    int sum=0;
    scanf("%d%d",&n,&k);
    for(int i=1; i<=n; ++i) {
        p[i].pre=i;
        p[i].relation = 0;
    }
    for(int i = 1; i <= k; ++i) {
        scanf("%d%d%d", &ope, &a, &b);
        if(a>n|| b>n) {
            sum++;
            continue;
        }
        if(ope == 2 && a == b) {
            sum++;
            continue;
        }
        root1 = find(a);
        root2 = find(b);
        if(root1 != root2) {
            p[root2].pre = root1;
            p[root2].relation = (3 + (ope - 1) +p[a].relation - p[b].relation) % 3;
        } else {
            if(ope == 1 && p[a].relation != p[b].relation) {
                sum++;
                continue;
            }
            if(ope == 2 && ((3 + p[b].relation - p[a].relation) % 3 != ope - 1)) {
                sum++;
                continue;
            }
        }
    }
    printf("%d\n", sum);
    return 0;
}

接下来就到了我们今日的重点——

线段树

定义：

　　线段树是一种二叉搜索树（实质是平衡二叉树），线段树的每个结点都存
储了一个区间，也可以理解成一个线段。

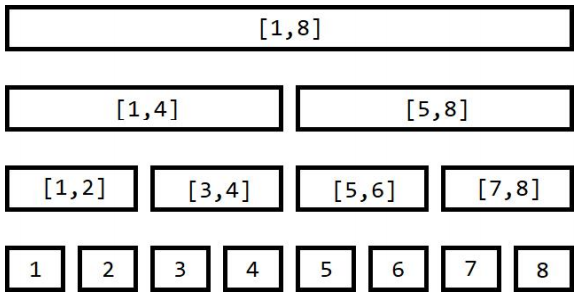
用途：

1.线段树的适用范围很广，可以维护修改以及查询区间上的最值、
求和。更可以扩充到二维线段树（矩阵树）和三维线段树（空间
树）。对于一维线段树来说，每次更新以及查询的时间复杂度为
O(log n)。
2.事实上，线段树多用于解决区间问题，但并不是线段树只能解决
区间问题。

看来前面以后，可能觉得线段树也没有那么难，很好理解。

确实，线段树概念很好理解，但有可能像本蒟蒻一样……

老师：“会了吗？”

我：“会！”。

老师：“真会了？”

我：“真会了！——吧”。

“线段树的思路和理解都木得问题，但这写代码就有些困难了”.

接下来就带大家写一下代码。。。。。。。

递归建树：

void build(int l,int r,int x) {
    if(l == r) tree[x].sum = a[l];
    else {
        int mid = l + ((r-l)>>1);
        build(l,mid, x<<1);
        build(mid+1,r, x<<1|1);
        pushup(x);
    }
}

单点修改：

#define lc x<<1
#define rc x<<1|1
#define mid ((l+r)>>1)
void pushup(int x) {
    tree[x].sum=tree[lc].sum+tree[rc].sum;
}
void update(int x,int l,int r,int p,int v) {
    if(l==r) {
        tree[x].sum=v;
        return;
    }
    if(p<=mid)update(lc,l,mid,p,v);
    else update(rc,mid+1,r,p,v);
    pushup(x);
}

区间查询求和：

int query(int x,int l,int r,int from,int to) {
    if(l>=from && r<=to)return tree[x].sum;
    int ans=0;
    if(from<=mid)ans+=query(lc,l,mid,from,to);
    if(to>mid)ans+=query(rc,mid+1,r,from,to); 
    return ans;
}

这里的pushup(x)是什么呢？

其实这就类似于爆搜中的回溯，但不是还原现场，

……

难说，举个栗子

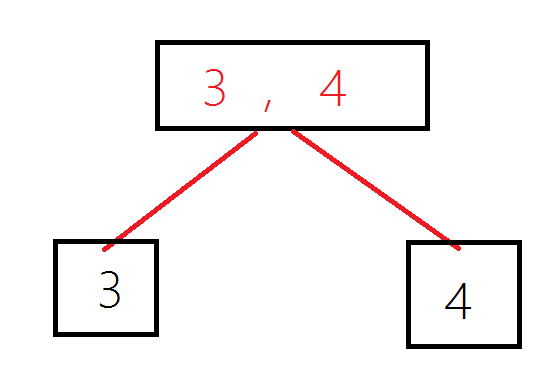
在上面，我们给区间下了一个懒标记，这个语句呢，

就相当于是将3，4这个区间往下一层，变成区间3和区间4.

下面看一下完整模板：

P3372 【模板】线段树 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上
求出某区间每一个数的和。

输入格式

第一行包含两个整数

第二行包含

接下来

1 x y k：将区间
2 x y：输出区间

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1

输出 #1

11
8
20

说明/提示

对于 $30\%30% 的数据：n \le 8n≤8，m \le 10m≤10。对于 70\%70% 的数据：n \le {10}^3n≤103，m \le {10}^4m≤104。对于 100\%100% 的数据：1 \le n, m \le {10}^51≤n,m≤105。$

保证任意时刻数列中任意元素的和在 $[-2^{63}, 2^{63})[−263,263) 内。$

【样例解释】

#include<bits/stdc++.h>
#define LL long long
using namespace std;
struct cs {
    LL ll,rr,vv;
} T[824290];
LL a[200005],v[824290];
LL n,m,x,y,z,sum,N;
void clean(LL x) {
    if(!v[x])return;
    T[x].vv+=(T[x].rr-T[x].ll+1)*v[x];
    if(T[x].ll!=T[x].rr) {
        v[x*2]+=v[x];
        v[x*2+1]+=v[x];
    }
    v[x]=0;
}
void maketree(LL x,LL y,LL num) {
    T[num].ll=x;
    T[num].rr=y;
    if(x==y) {
        T[num].vv=a[x];
        return;
    }
    maketree(x,(x+y)/2,num*2);
    maketree((x+y)/2+1,y,num*2+1);
    T[num].vv=T[num*2].vv+T[num*2+1].vv;
}
void inc(LL x,LL y,LL z,LL num) {
    clean(num);
    if(x<=T[num].ll&&T[num].rr<=y) {
        v[num]+=z;
        return;
    }
    T[num].vv+=(min(y,T[num].rr)-max(x,T[num].ll)+1)*z;
    if(T[num].ll==T[num].rr) return;
    int mid=(T[num].ll+T[num].rr)/2;
    if(x>mid)inc(x,y,z,num*2+1);
    else if(y<=mid)inc(x,y,z,num*2);
    else {
        inc(x,y,z,num*2);
        inc(x,y,z,num*2+1);
    }
}
void out(int LL,int LL,LL num) {
    clean(num);
    if(x<=T[num].ll&&T[num].rr<=y) {
        sum+=T[num].vv;
        return;
    }
    int mid=(T[num].ll+T[num].rr)/2;
    if(x>mid)out(x,y,num*2+1);
    else if(y<=mid)out(x,y,num*2);
    else {
        out(x,y,num*2);
        out(x,y,num*2+1);
    }
}
int main() {
    scanf("%d%d",&n,&N);
    for(int i=1; i<=n; i++)scanf("%d",&a[i]);
    maketree(1,n,1);
    for(int i=1; i<=N; i++) {
        scanf("%d%d%d",&m,&x,&y);
        if(m==1) {
            scanf("%d",&z);
            inc(x,y,z,1);
        } else {
            sum=0;
            out(x,y,1);
            printf("%lld\n",sum);
        }
    }
    return 0;
}

线段树的代码普遍都很长，不像DP，所以线段树的区间删除、

区间求和、改变区间……都需要我们“背”；

posted on 2022-07-26 20:46 博然后深阅读(87) 评论(0) 编辑收藏举报

刷新页面返回顶部

导航

2022.7.26学习笔记

主要内容：

堆

定义：

种类：

优先队列：

并查集

定义：

例题：

P2024 [NOI2001] 食物链

题目描述

输入格式

输出格式

输入输出样例

说明/提示

线段树

定义：

用途：

递归建树：

单点修改：

区间查询求和：

P3372 【模板】线段树 1

题目描述

输入格式

输出格式

输入输出样例

说明/提示