用规划模型求解指派问题
一、前言
优化模型主要有线性规划、非线性规划、动态规划和整数规划。而指派问题是整数规划中一类重要的问题:
有\(n\)项任务,由\(n\)个人来完成,每个人只能做一件,第\(i\)个人完成第\(j\)项任务要\(c_{ij}\)小时,如何合理安排时间才能使总用时最小?
二、 指派问题的数学模型
我们引入 0 - 1变量 \(x_{ij}\)
用x_{ij}表示第i个人完成第j项工作所需要的资源数,称之为价值系数。因此指派问题的数学模型是:
- 第一个式子表示完成全部n项工作所消耗的总资源数要最少;
- 第二个式子表示第i个人只完成一项工作;
- 第三个式子表示第j项工作只能由一个人完成;
- 第四个式子表示决策变量只能取0或者1。
指派问题可以看作0 - 1整数规划问题来求解,也可以用更简单的匈牙利算法来求解。
三、 0 - 1规划求解(Matlab)
我们先给出这样一个例题,图中数值为第i个人要完成第j个任务需要消耗的资源数\(x_{ij}\),求解:如何安排才能使的总资源消耗最少。
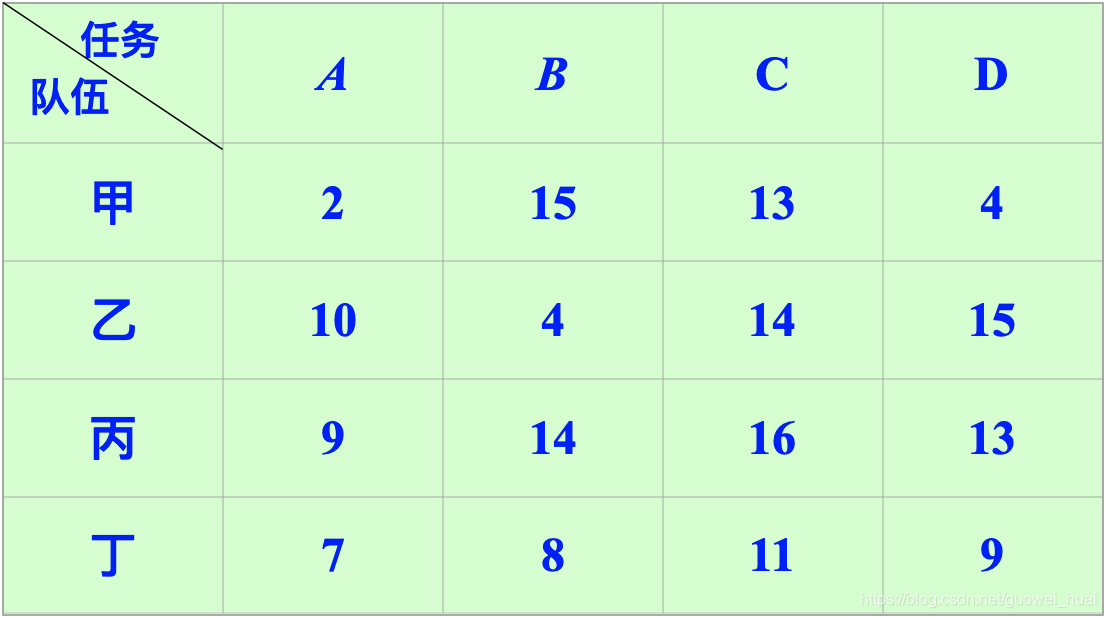
编程思路:
根据规划问题的要求:
每个人只能完成一个任务,每个任务只能由一个人完成。也正如第三部分中的第二个式子和第三个式子,当该4x4矩阵表示\(x_{ij}\),即指派第i个人完成第j个任务时,此时每一行相加的值和为1,每一列相加的值和为1。(\(x_{ij}\)的值只能为0或者1)根据该思路,我们可以来进行Matlab变成。
c=[2,15,13,4,10,4,14,15,9,14,16,13,7,8,11,9]';
Aeq=[1,1,1,1,0,0,0,0,0,0,0,0,0,0,0,0;
0,0,0,0,1,1,1,1,0,0,0,0,0,0,0,0;
0,0,0,0,0,0,0,0,1,1,1,1,0,0,0,0;
0,0,0,0,0,0,0,0,0,0,0,0,1,1,1,1;
1,0,0,0,1,0,0,0,1,0,0,0,1,0,0,0;
0,1,0,0,0,1,0,0,0,1,0,0,0,1,0,0;
0,0,1,0,0,0,1,0,0,0,1,0,0,0,1,0;
0,0,0,1,0,0,0,1,0,0,0,1,0,0,0,1];
beq=[1;1;1;1;1;1;1;1];
lb=zeros(16,1);
ub=ones(16,1);
[x,fval] = linprog(c,[],[],Aeq,beq,lb,ub)
x=reshape(x,[4,4])'
其中Aeq和beq代表的是等式约束,Aeq的前四行分别表示 4x4的\(x_{ij}\)矩阵中四行中每行相加的值为1;Aeq的后四行分别表示4x4的\(x_{ij}\)矩阵找那个的四列中每列相加的值为1。(实际上它就是将4x4的矩阵按照行进行展开成了1x16的矩阵)。
然后再调用linprog()线性规划的函数,输入相应参数进行求解。求解所得的x是16x1的矩阵,我们为了便于观察,最后将该矩阵转换成4x4的矩阵。
以上代码也可以用for循环对其优化,将线性规划转换成整数规划进行求解
c=[2,15,13,4;10,4,14,15;9,14,16,13;7,8,11,9];
c=c(:);a=zeros(8,16);intcon=1:16;
for i=1:4
a(i,(i-1)*4+1:4*i)=1;
a(4+i,i:4:16)=1;
end
b=ones(8,1);lb=zeros(16,1);ub=ones(16,1);
x=intlinprog(c,intcon,[],[],a,b,lb,ub)
x=reshape(x,[4,4])
在对于指派问题中,还有一个经典算法时匈牙利算法,核心是寻找增广路径,用增广路径求二分图最大匹配的算法。后面会有一篇博客专门分享我对匈牙利算法理解及matlab实战。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号