Zero-Shot Learning 最新研究进展

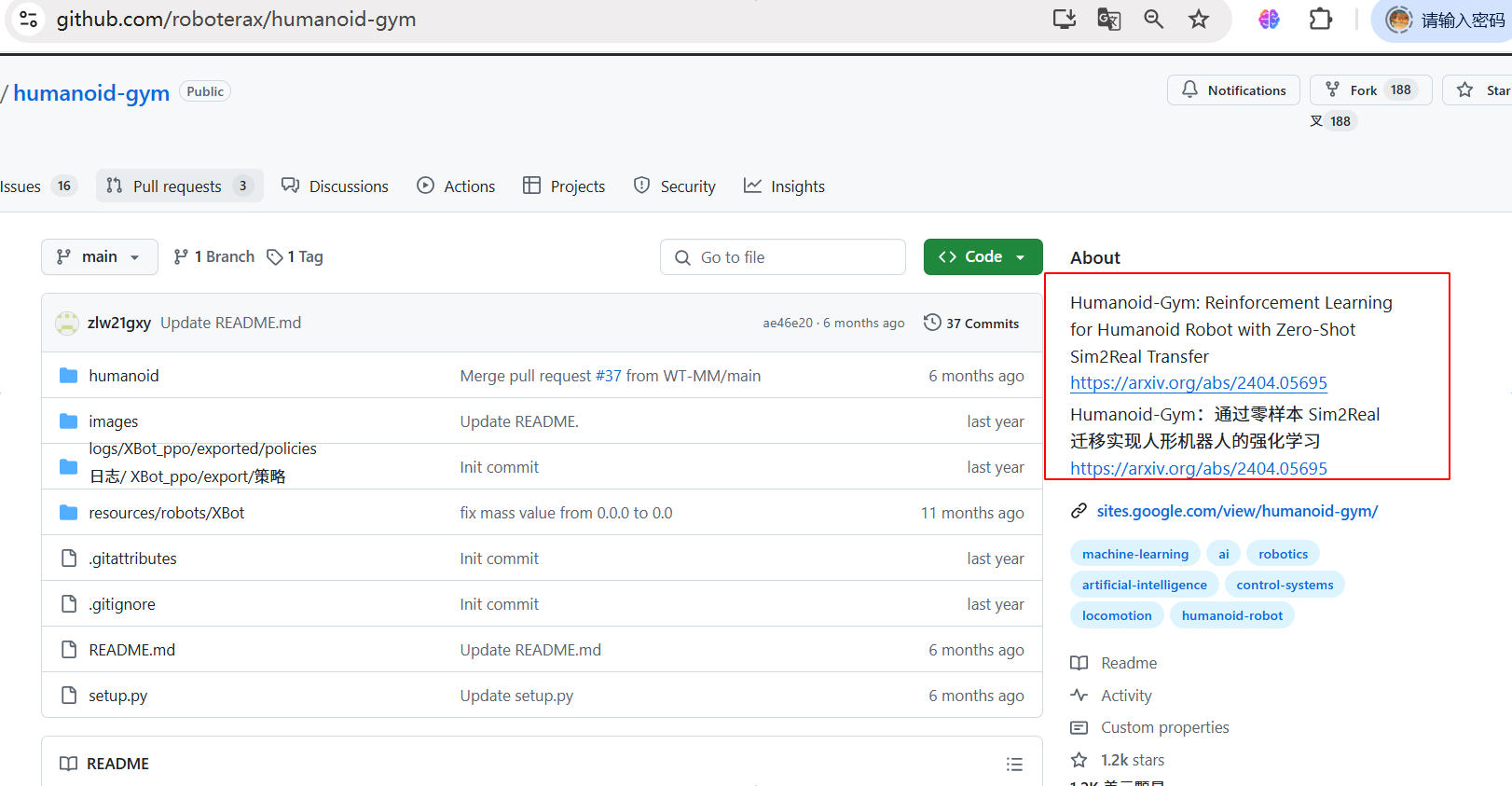
结合强化学习的零样本学习是目前机器人应用的一个热门方向。==》alpha go-》alpha zero。因为有现实世界的反馈。

这篇论文《Zero-Shot Learning of Causal Models》的核心分析要点和方法总结如下：

主要背景

目标问题：
- 传统因果模型结构（SCM）的识别和学习，通常需要为每个数据集单独训练一个生成模型，增加了模型的复杂性和训练成本。
- 本文目标是开发一种单一模型，在零样本（Zero-Shot）的条件下，从观察数据中推断因果模型，并能够对不同分布的数据集泛化。
提出的方法：
- 本研究在之前 FiP（Fixed-Point方法）的基础上，提出了Cond-FiP（Conditional Fixed-Point Decoder）。
- 使用条件推断机制，将数据嵌入表示作为输入，从而直接解码出结构因果模型（SCM）的生成机制。

核心方法

Cond-FiP模型结构由两个关键模块组成：

数据集编码器（Dataset Encoder）：
- 将观测数据 $DXDX 和因果图 GG 转换为嵌入表示 E(L(DX),G)E(L(DX),G)。$
- 嵌入信息提供条件上下文，用于推断因果关系。
条件FiP解码器（Conditional FiP Decoder）：
- 与编码器生成的嵌入表示相结合，直接推理每个数据集对应的SCM的因果生成机制。
- 支持生成新的观察样本和干预样本。

推断流程：

通过联合训练，Cond-FiP学习因果推断模型，然后在测试阶段以零样本方式处理新数据。

关键实验与分析

实验设置：
- Cond-FiP的性能被分别测试于合成数据集和真实数据集，任务包括因果模型推断、样本生成、干预预测等。
- 对比基线包括：
  - CausalNF
  - FiP（固定点方法的原始版本）
  - DoWhy（其他因果推断方法）
实验结果：
- 泛化性：
  - Cond-FiP在训练时仅使用小型数据集（400样本），但能在测试时推广到更大规模（1000样本）的任务中。
  - 较少的训练样本显著优于基线模型，其零样本推断能力凸显。
- 分布迁移的鲁棒性：
  - 对因果机制的分布变化表现出高度鲁棒性，性能基本未受影响。
  - 然而，在噪声变量的分布迁移下，性能会逐渐下降，反映了对噪声的敏感性。
- 对比研究：
  - Cond-FiP在所有任务（如生成新样本、干预实验中生成样本）中，均优于CausalNF和FiP。
  - 对于更大规模结构图（>20节点）的任务，基线模型（如CausalNF）性能大幅下降，而Cond-FiP表现保持稳定。
稀缺数据性能：
- 在有限样本（稀缺数据）下的实验表明：
  - 对比需要训练的传统方法，Cond-FiP能保持良好的泛化能力，利用先验学习的归纳偏置有效应对数据稀缺场景。
消融实验（Ablation Study）：
- 编码器：若仅在训练中使用线性函数关系（LIN）或特定非线性函数（RFF）的数据进行训练，模型仍能得出较优结果，但结合两种功能关系的数据训练整体效果更强。
- 解码器：使用多类型关系训练效果明显优于单一关系，显示多样数据对模型泛化能力的提升。

局限性与改进建议

扩展性限制：
- Cond-FiP在较大规模上下文（如大数据量或更复杂因果结构）时性能提升有限。
- 为进一步提高性能需要扩展模型及训练数据的规模。
对噪声分布的敏感性：
- 噪声变量显著变化时表现欠佳，可作为进一步改进的重点。

总结

创新性：这是首次在零样本条件下实现因果生成模型（SCM）的推断，展现了Cond-FiP强大的泛化能力与任务鲁棒性。
未来方向：进一步拓展Cond-FiP到实际应用场景，特别是扩充更大规模因果网络，探索更复杂的分布配置和真实数据问题。

相关工作主要涉及了几个领域，其中包括因果模型（SCM）学习、零样本推断（Zero-Shot Learning）、因果发现和生成模型等内容。以下是部分重要的相关工作与贡献：

1. 与零样本学习和因果模型学习相关的工作

Lorch et al. (2022): 提出了用于因果结构学习的模型，采用了变换器（transformers）架构，并通过合成数据集的采样来实现监督式结构学习。
Ke et al. (2022, 2023): 涉及基因调控网络的因果学习（如Discogen），也研究了通过零样本方式学习因果结构的方法。
Scetbon et al. (2024): 提出了固定点方法（FiP）的改进版 Cond-FiP，用于学习生成因果模型，尤其关注加性噪声因果模型（AN-SCMs）的功能机制推测。

2. 生成性模型和结构发现

Khemakhem et al. (2021): 在自回归因果流建模中首次将因果生成过程连接为三角输入映射，并扩展为更灵活的广义因果模型。
Zheng et al. (2018): 提出了用于因果结构发现的连续优化方法 DAGS，研究因果图的无环性约束。
Lachapelle et al. (2019): 研究了基于梯度优化的神经网络因果图学习方法。

3. 因果表示学习与稳健性

Schölkopf et al. (2021): 在因果表示学习中提出了进一步的理论基础，包括因果学习模块对跨分布能力的提升。
Wu et al. (2024): 提出了处理因分布外（OOD）推广问题的合成多数据集因果模型结构估计方法。

4. 实验与实证研究

文档中还讨论了 Cond-FiP 在稀疏数据环境下的性能研究，以及对分布偏移的敏感性。其中强调了以下两点：

稀少数据设定（Appendix D）：Cond-FiP 因其归一化学习过程，在数据稀缺环境下表现优于现有方法。
分布偏移测试（Appendix E.3）：虽然 Cond-FiP 对噪声变量的偏移较为敏感，但其对因果机制的偏移仍保持稳健。

5. 其他关键相关文献

Pearl (2009): 核心的因果推理经典著作《Causality》。
Peters et al. (2017): 《因果推断元素：基础和学习算法》，提供因果图学习的理论框架。
Vaswani et al. (2017): 关于注意力机制与变换器模型（transformers）的基础论文。

这些相关研究为因果发现的零样本学习打下了理论与实践基础，同时也阐明了现有领域的局限性：多数研究需要为每个数据集单独训练生成模型，难以实现知识共享。Cond-FiP 的提出正是为了解决这类问题，通过归一化训练的方式实现跨数据集的因果知识推断能力。

1. Cond-FiP 方法的高层伪代码

Cond-FiP 的核心是将数据集嵌入以及基于固定点推断因果机制的模型结合，通过一个共享模型实现对多个数据集的推断能力。

# 输入: Observational data D_X, causal graph G  
# 输出: Inferred functional mechanisms F or new samples from SCM  

def cond_fip_pipeline(data, causal_graph):  
    """  
    Cond-FiP execution pipeline.  
    """  
    # Step 1: Dataset Embedding via Encoder  
    embeddings = dataset_encoder(data, causal_graph)  
    
    # Step 2: Conditional Fixed Point Inference  
    inferred_mechanisms = cond_fip_decoder(embeddings, causal_graph)  
    
    # Step 3: Optional Sample Generation  
    new_samples = generate_samples(inferred_mechanisms, intervention=False)  
    return inferred_mechanisms, new_samples

2. 数据集编码器

数据集编码器旨在将观察数据和因果图的信息映射到潜在的嵌入空间中。

def dataset_encoder(data, causal_graph):  
    """  
    Encodes data and causal graph into latent embeddings.  
    """  
    # Step 1: Extract noise embeddings from data using ANM assumptions  
    latent_noise = infer_noise(data, causal_graph)  
    
    # Step 2: Use embeddings to represent the dataset  
    embeddings = neural_network(latent_noise, causal_graph)  
    return embeddings

关键步骤解释：

利用加性噪声模型 (ANM) 假设从观测数据中推断噪声变量。
利用一个神经网络基于噪声和因果图生成数据集的潜在表示。

因果图是结构因果模型（SCM，Structural Causal Model）的一部分，用来表示变量之间的因果关系，其中通常采用有向无环图（DAG, Directed Acyclic Graph）形式。这些因果图描述系统中随机变量之间的因果依赖结构，其中每个变量既可能由其他变量因果决定，又受其自身的噪声变量影响。

在文件内容中提及了因果图用于以下场景：

因果推断与生成模型：
文件提到了通过条件固定点推导（Cond-FiP）推断 SCM 的功能机制时，需要有因果图作为输入或上下文信息。Cond-FiP 方法允许在未知因果图信息的前提下通过观测样本反推出因果图结构。
利用 DAG 表示因果关系：
因果图中的节点表示随机变量，边表示因果作用。因果图所定义的 DAG 可以用于揭示数据生成机制（例如，某些变量如何通过函数关系和噪声变量相互影响生成观测值）。
因果发现的研究：
文档提到了一些现有文献利用优化方法或神经网络架构（如 FiP、AVICI）从观测数据中恢复因果图。

3. 条件固定点解码器 (Cond-FiP Decoder)

推断数据集的函数机制。通过条件固定点求解器，结合嵌入条件来估计生成因果模型的函数。

def cond_fip_decoder(embeddings, causal_graph):  
    """  
    Infers functional mechanisms using a conditional fixed-point scheme.  
    """  
    # Step 1: Initialize noise conditionally  
    noise = initialize_noise(embeddings, causal_graph)  
    
    # Step 2: Iteratively solve the fixed-point problem  
    for _ in range(max_iterations):  
        noise = apply_fixed_point_update(noise, embeddings, causal_graph)  
    return extract_functions_from_noise(noise)

关键步骤解释：

嵌入和因果图信息决定固定点的初始条件。
使用迭代算法更新解，直到满足固定点条件。
最终从固定点噪声变量中提取生成机制。

4. 生成新数据样本

可以使用 Cond-FiP 推断出的功能机制生成对应的观察样本或干预样本。

def generate_samples(function_mechanisms, intervention=True):  
    """  
    Generates samples from the inferred SCM.  
    """  
    if intervention:  
        functions = apply_intervention(function_mechanisms)  
    else:  
        functions = function_mechanisms  
    
    # Sample noises and apply generative functions  
    noise_samples = sample_noise(functions)  
    samples = apply_mechanisms(noise_samples, functions)  
    return samples

5. Cond-FiP 训练目标 (高层公式)

训练的目标是最小化以下损失（具体参考论文公式）：

math 
L = E_S ~ ||F(D_X) - H∘E(L(D_X), G)||^2 

伪代码实现

def training_objective(data, causal_graph, encoder, decoder):  
    """  
    Defines and computes the training objective.  
    """  
    # Step 1: Encode dataset embeddings  
    embeddings = encoder(data, causal_graph)  
    
    # Step 2: Decode functional mechanisms  
    inferred_mechanisms = decoder(embeddings, causal_graph)  
    
    # Step 3: Compute loss compared to true SCM mechanisms  
    true_mechanisms = get_ground_truth_mechanisms(data)  
    loss = compute_loss(inferred_mechanisms, true_mechanisms)  
    return loss

posted @ 2025-04-10 20:17 bonelee 阅读(151) 评论(0) 收藏举报

刷新页面返回顶部

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。

Zero-Shot Learning 最新研究进展

主要背景

核心方法

关键实验与分析

局限性与改进建议

总结

1. 与零样本学习和因果模型学习相关的工作

2. 生成性模型和结构发现

3. 因果表示学习与稳健性

4. 实验与实证研究

5. 其他关键相关文献

1. Cond-FiP 方法的高层伪代码

2. 数据集编码器

关键步骤解释：

3. 条件固定点解码器 (Cond-FiP Decoder)

关键步骤解释：

4. 生成新数据样本

5. Cond-FiP 训练目标 (高层公式)

伪代码实现

公告