面向开放世界的少样本学习：回顾与展望【2024.8】

https://arxiv.org/abs/2408.09722

摘要

本研究深化了开放世界中的小样例学习（Few-Shot Learning, FSL）技术，通过回顾相关领域最新成果，提出了一个统一的分类框架——开放世界小样例学习（OFSL）。该框架将问题划分为实例变化、类别变化及分布变化三个主要场景，并对每一类别下的方法进行解析与比较。此外，本文标准化了实验设置和评估指标，提出了关键挑战与未来研究方向。

关键点

小样例学习旨在模仿人类通过少量样本快速学习新概念的能力，但传统方法依赖于静态、干净的完整数据而不适配开放世界的动态环境。
开放世界小样例学习涵盖了三大场景：实例变化、类别变化及分布变化，并明确相关技术的优势及限制。
在实例变化场景中，研究重点在噪声样本处理和开放集测试实例分类，其策略主要分为参数优化和样本选择。
类别变化研究主要关注增量学习中如何保持旧类知识与学习新类之间的平衡，并引入数据策略、网络集成及特征正则化等方法。
分布变化研究聚焦跨领域小样例学习，通过数据增强、参数优化和特征处理等方法来缓解域间偏移问题。
本研究对典型算法进行了实验比较与性能分析，揭示出不同问题场景和方法间的显著差异。
提出了开放世界小样例学习中的若干未来方向，如多标签学习、抵御对抗攻击及不平衡分类的研究。

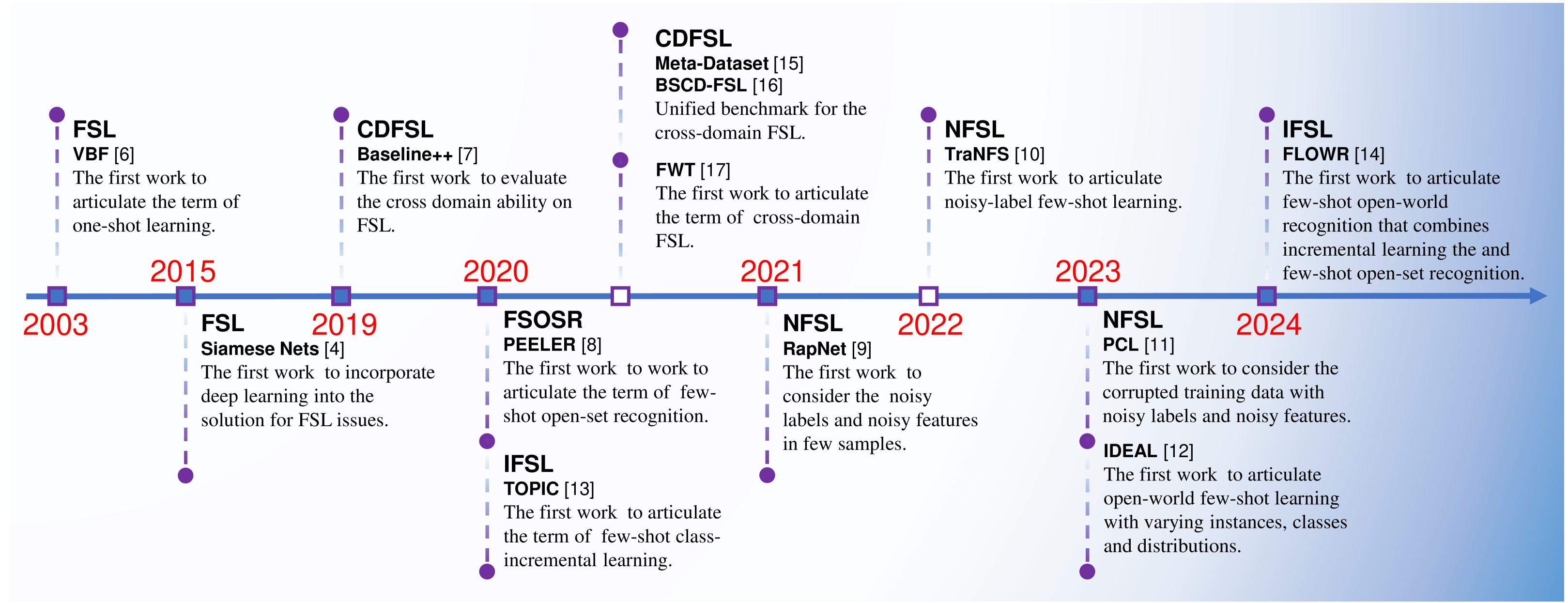
根据提供的文档内容，目前业界关于小样本学习（Few-Shot Learning，FSL）的相关工作可以归纳为以下几类主要方向：

1. 传统小样本学习

目标：提高机器在仅有少量样本的情况下学习和泛化的能力。
核心方法：
- 度量学习：例如Siamese networks和Matching networks，将相似性学习用于样本分类。
- 元学习（Meta-Learning）：学习一种快速适应新任务的学习能力。
- 数据增强：通过生成伪造数据增强小样本学习效果。

2. 开放世界小样本学习（Open-World Few-Shot Learning，OFSL）

挑战：现实世界数据的不确定性、动态性与不完整性。
分类场景：
- 变化实例（Varying Instances）：
  - 噪声小样本学习（Noisy Few-Shot Learning, NFSL）：处理训练过程中样本特征或标签被噪声污染的问题。
  - 开放集识别（Few-Shot Open-Set Recognition, FSOSR）：应对测试数据中存在未知类别的情况。
- 变化类别（Varying Classes）：
  - 增量学习（Incremental Few-Shot Learning, IFSL）：需要持续学习新类别，同时保持旧类别知识。
- 变化分布（Varying Distributions）：
  - 跨域小样本学习（Cross-Domain Few-Shot Learning, CDFSL）：源域和目标域分布存在显著差异的情况下进行学习。
相关技术：
- 数据策略：包括实例复现（Instance Rehearsal）与使用无标签数据。
- 网络集成：结合不同功能的模型，包括双流模型与文本指导。
- 特征正则化：通过约束特征分布来实现增量学习的稳定性。

3. 跨域小样本学习

目标：解决源域和目标域之间因分布差异（域偏移）导致的学习性能下降。
方法：
- 特征对齐：如跨域对抗学习及特征变换。
- 数据增强：通过生成源-目标域共享特征增强学习效果。

4. 噪声鲁棒性与类别不平衡

噪声鲁棒性：
- 学习抗噪能力以应对标签或特征被污染的情形（例如Dual-Level Curriculum Meta-Learning方法）。
类别不平衡：
- 提出随机类别任务设计和重采样策略以适应类别数量高度不均的场景。

5. 数据增强与生成模型

数据增强采用生成模型（如GANs）生成伪样本以提高罕见类别的训练效果。
辅助信息方法利用外部输入（如文本描述）丰富原始训练样本。

6. 近期发展与未来方法

领域引入了多个新方向，如跨域小样本视觉识别、基于贝叶斯嵌入的开放世界识别等。
未来研究方向：
- 探索更强大的跨域方法，改进数据不平衡场景下的学习能力。
- 提高模型防御对抗攻击和处理开放集未知类别的鲁棒性。
- 应用于更具挑战性的场景，如多任务学习及多标签设置。

从文档中可提取出一些关于近期小样本学习（Few-Shot Learning, FSL）在开放世界中的发展趋势和未来研究方向。以下是更详细的总结和展开：

近期发展领域

开放世界小样本学习的场景扩展
- 小样本学习逐渐从封闭世界转向更复杂和动态的开放世界场景，针对数据的动态性、不完整性和噪声特性提出了相应方法。
- 关键子方向：
  - 跨域小样本学习（Cross-Domain FSL, CDFSL）：解决源域和目标域的分布差异导致的迁移问题。
  - 增量小样本学习（Incremental FSL, IFSL）：要求模型在学习新类别时保持旧知识的稳定性。
  - 开放集小样本学习（Few-Shot Open-Set Recognition, FSOSR）：处理测试集中出现未知类别的情况。
  - 噪声小样本学习（Noisy FSL, NFSL）：应对训练数据中存在噪声样本的问题。
方法论优化
- 数据增强策略：
  - 通过生成模型方法（例如GANs）或引入辅助信息（如文本、外部知识）增强训练样本。
  - 示例：MORGAN生成模型可以模拟未知类别样本分布。
- 度量评估方法：
  - 修正距离和密度分布以优化特征空间。
  - 示例：PEELER、GEL等方法通过能量分布或对比性学习优化类别边界。
- 特征处理技术：
  - 特征变换、正则化或特征选择。
  - 示例：基于正交基的特征分布约束可减少新旧任务之间的干扰。
面向不确定性的数据建模
- **贝叶斯方法（Bayesian Methods）**引入了概率表征以处理不确定性。
- 示例：Bayesian embeddings 已应用于开放集的未知类别分布建模。
任务优化
- 技术框架包括元学习（Meta-Learning）、双流网络（Bi-Stream Networks）以及利用内外部特征的多模态学习技术。
- 增量学习中强调通过带记忆的实例回放（如SPPR）维持旧类知识。

未来研究方向

1. 更复杂的任务与场景

多任务学习：整合模态间的知识共享（例如图像和文本）以解决复杂的开放场景问题。
多标签学习：目前多数方法假设每个样本只属于一个类别，而现实中可能面临多标签任务。
跨模态增强：在图像、文本、语音等多模态之间实现联合学习和增强。

2. 更鲁棒的小样本方法

噪声与对抗性：
- 在高噪声或强对抗性条件下，提升模型的鲁棒性。
- 探索对抗训练和数据去噪策略。
泛化能力的提升：
- 提高跨域泛化能力，特别是针对分布不连续或分布大幅改变的场景，如开放集分类。

3. 跨域迁移与分布变化

动量对抗学习：替代传统的特征翻译方法，在无法确定目标域分布的情况下进行迁移。
分布偏移自适应：改进模型的动态域适应能力，使其对分布变化更加敏感。

4. 数据高效与弱监督方法

无标签与弱监督学习：
- 对未标注数据进行高效利用，例如通过自监督和伪标签生成。
- 半监督学习（Semi-Supervised Learning）补充标注稀缺的问题。
标签敏感网络：减少对精细标签的依赖，允许粗粒度标签指导小样本学习。

5. 开放集识别未知类别

探索未知样本分布：
- 构建更强的模型以预测未知类分布，进一步提升开放集识别的精度。
- 示例：MORGAN、ProCAM等方法在生成对未知类探索具有潜力。
优化决策边界：
- 通过混合多变量方法（密度与能量评估结合）优化已知与未知类别的辨识能力。

6. 实验基准与公平评估

通用评测基准的建立：
- 当前的研究常采用独立数据集，未来需要统一的实验和评测框架，例如Meta-Dataset（包含多个领域数据）。
标准化评价指标：
- 当前评价方法集中于精度和召回率，未来需要新增综合指标如鲁棒性度量、泛化难度等。

根据文章分析和实验内容，该文总结了开放世界中小样本学习（Few-Shot Learning, FSL）的研究现状，并通过对三个主要开放世界场景的实验对比，揭示了一些关键发现和结论：

实验内容与数据：

1. 开放集小样本学习（Few-Shot Open-Set Recognition, FSOSR）

目标：在测试集中识别未知类别样本的能力。
关键方法：
- 度量方法（Metric-Based Methods）：如GEL（通过全局能量分配来检测未知类别）。
- 数据方法（Data-Based Methods）：如proCAM（通过生成虚拟样本模拟开放环境）。
- 特征方法（Feature-Based Methods）：如ATT（通过变换函数生成负原型表示未知类别）。
实验结果：
- 度量方法的性能在稳定性和表现上优于其他方法。
- 例如，GEL表现最佳，因为它在类别和像素层面上分析开放样本差异，精准识别未知类。
- 特征方法中的ATT模型利用语义信息生成未知类别边界，性能也表现优异。

2. 增量学习（Incremental Few-Shot Learning, IFSL）

目标：在学习新任务的同时保留对旧任务的学习效果（避免灾难性遗忘）。
关键挑战：
1. 灾难性遗忘：学习新知识时丢失旧知识。
2. 稳定性-灵活性困境：固定模型参数有益于保留旧知识，但限制新任务的学习效率。
关键方法：
- 数据策略（Data Strategy）：如实例重复（SPPR）和引入无标签数据。
- 网络集成（Network Ensemble）：如元学习与双流网络（Bi-Stream Networks）。
- 特征正则化（Feature Regularization）：如正交分解方法（避免新知识干扰旧知识表示）。
实验结果：
- 使用正交基的方法（如SubRe、WaRP）能够有效缓解灾难性遗忘。
- 网络集成和特征正则化方法在保留旧知识的同时提高新知识的学习效果。

3. 跨域小样本学习（Cross-Domain Few-Shot Learning, CDFSL）

目标：解决源域和目标域分布不同的情况下学习过程的有效性。
关键方法：
- 数据增强（Data Augmentation）：通过生成目标域样本（如StyleAcdv）提升泛化能力。
- 参数优化（Parameter Optimization）：通过调节域间参数（如SWP）提高模型在目标域上的性能。
- 特征处理（Feature Processing）：如特征选择与融合，优化域间共享特征。
实验结果：
- 参数优化方法在大部分数据集上优于其他方法（如ResNet10上的SWP）。
- 数据增强方法（如使用对抗生成样本的StyleAcdv）表现出较强的泛化能力。

关键发现：

度量方法在开放集场景中的稳定性和效率优于数据和特征方法。
增量学习中，正交基方法和网络集成方法的组合能够有效缓解旧知识遗忘问题。
在跨域场景下，引入目标域的任务或风格数据能显著提高模型的跨域适应能力。
不同方法的表现与场景复杂性相对应，固定假设（如类别边界）可能影响小样本学习效果。

度量方法（Metric-Based Methods）是在小样本学习（Few-Shot Learning, FSL）中常见的一类方法，特别是在开放世界小样本场景中用于解决 Few-Shot Open-Set Recognition (FSOSR) 问题。这些方法通过构建一个能够区分已知类别和未知类别的特征空间，利用距离测量或分布校准来判断输入样本的类别归属。

度量方法的核心思想

特征空间构建：为每个类别生成特定的特征表示，在高维嵌入空间中描述样本之间的关系。
度量计算：通过测量支持集（Support Set）样本和查询样本（Query Set）之间的特定度量（如距离或相似性），进行类别预测和未知类别识别。
对未知类别的处理：通过调整距离或特征分布，显式或隐式地划定已知类别与未知类别的边界。

这些实验数据和结论有助于推动开放世界小样本学习领域的发展，并明确了未来研究的几个方向，包括：

强化跨域迁移能力。
优化模型应对未知类别的鲁棒性。
改进正则化方法以更好地保留知识。

Bayesian Embeddings 的原理

贝叶斯嵌入模型的核心思想在于利用概率分布表征样本和类别，以处理开放世界中的不确定性。在开放世界场景下，系统需要应对以下问题：

已知类别数据稀缺：小样本学习使得难以精准定义已知类别的分布。
未知类别的存在：测试集中可能含有未知类别样本，无法简单依靠传统距离度量或分类器确定类别。
跨领域或分布变化：源域与目标域导致类别分布和特征分布不一致。

贝叶斯嵌入在此情景下的优点在于：

通过概率表示样本特征：用一个概率分布（如正态分布）来表示每个类别的样本，而不是固定的特征点。
建模不确定性：通过对类别分布的估计量化样本之间的相似性和未知类别的检测概率。
多样性兼容：适用于小样本、跨域和开放世界场景，不需要过多先验信息。

该方法涉及以下核心部分：

生成分布：为每一个类别学习一个隐变量分布，以描述类别内样本特征的多样性。
相似性计算：基于 KL 散度（Kullback-Leibler Divergence）或其他统计距离度量算出查询样本与类别分布之间的相似性。
拒绝未知类别：以超出某一相似度阈值范围为标准，过滤未知类别的样本。

具体方法与实现

类别表示为概率分布：
- 每个类别的嵌入表示采用一个高斯分布 $N(μ,Σ)N(μ,Σ)，其中 μμ 是类别的聚类中心，ΣΣ 是类别的协方差矩阵，表示分布的不确定性。$
- 系统通过极大似然估计（Maximum Likelihood Estimation）学习最佳的 $(μ,Σ)(μ,Σ) 参数。$
计算查询样本的分类概率：
- 查询样本 $xqxq 被映射到一个概率分布中，利用贝叶斯公式比较它与已知类别分布 N(μ,Σ)N(μ,Σ) 之间的匹配程度。$
- 使用 KL 散度或马氏距离（Mahalanobis Distance）衡量分布之间的不匹配程度，并据此判定 $xqxq 属于哪个已知类别，或者是否属于未知类别。$
拒绝未知类别：
- 使用概率阈值或不确定性指标（例如高于某个 KL 散度值表示未知类别），自动标记和拒绝不属于任何已知类别的样本。
分布校准：
- 在开放世界场景中，为了适应分布漂移和未知类别样本，系统会动态校准基于贝叶斯推断的类别分布参数。

优势与特点

优雅地处理不确定性：
- 由于贝叶斯嵌入建模了样本特征的概率分布，它能够自然地处理小样本数据中的高不确定性问题。
适应开放世界的需求：
- 允许系统对属于未知类别的样本进行拒绝（开放集识别），克服传统方法无法处理未知类别的局限性。
良好的泛化能力：
- 贝叶斯模型通过分布学习跨域和跨任务的特征，使其在小样本和跨领域场景中表现优秀。
鲁棒性强：
- 在高噪声、分布漂移或数据不完整的场景中具有很强的适应能力。

实验结果和表现

根据文章中的陈述，贝叶斯嵌入方法在以下基准任务中的表现显著提升：

小样本开放集识别任务：在既确保已知类别的分类性能的同时，大幅提高了对未知类别的拒绝率。
跨域小样本学习任务：通过贝叶斯推断校准目标域分布，有效减少了跨域性能下降问题。
性能对比：相比于传统的度量学习方法（如 Prototypical Networks 等），贝叶斯嵌入方法在开放集 AUROC（Area Under the Receiver Operating Characteristic Curve）指标上提升显著，另外在分类准确性（Accuracy）和未知拒绝率上表现更为均衡。

未来改进和研究方向

更复杂分布表示：
- 当前研究中经常使用简单高斯分布来表示类别特征，未来可以扩展到更复杂的混合分布（例如混合高斯模型，GMM）。
未知类别的生成：
- 尝试结合生成模型（如 GAN 或 VAE）来主动模拟未知类别分布，并通过贝叶斯方法进行联合优化。
多模态学习：
- 引入多模态数据（如文本、图像语义信息）在贝叶斯框架内进行联合建模，提高特征表示的可靠性。
开放世界持续学习：
- 尝试逐步更新贝叶斯分布（在线学习）以适应开放世界场景中动态变化的任务。

总结

Bayesian Embeddings 是开放世界小样本学习中的一种创新方法，它通过建模不确定性和概率分布，有效应对未知类别检测、数据稀缺和分布变化等挑战。这种方法在开放集识别、小样本分类和跨域迁移任务上的卓越表现揭示了其广阔的应用前景，同时也为未来研究指出了新的方向。

元学习（Meta-Learning，也称为“学习如何学习”）是机器学习中的一种方法论，其目标是通过元任务的训练，让模型具备快速适应新任务的能力，尤其是在数据量非常有限（例如小样本学习，Few-Shot Learning）的情况下。这种方法的核心思想是利用多个任务的共享经验来加速新的任务学习过程。

根据您上传的文档中可能提及的内容，以及对元学习领域的整体理解，可以详细介绍如下：

元学习的核心思想

与传统机器学习专注于单一任务的训练不同，元学习试图从一个任务集合的经验中学习通用特性。元学习由两层结构组成：

元任务学习（Meta-Learning）：
- 在任务集合（task distribution）上进行训练，学习一个适用于不同任务的通用模型初始化、更新规则或特征表示。
任务层学习（Task-Level Learning）：
- 利用元学习的经验，通过少量样本快速完成特定任务。

元学习的目标是：基于从多个任务的训练中学到的规律，让模型在仅需少量样本或少量更新的情况下，就能够在新任务上表现出色。

元学习的方法分类

元学习的具体方法可以根据其学习的目标和方式，分为以下三类：

1. 基于优化的元学习（Optimization-Based Meta-Learning）

这类方法的核心是学习模型的优化过程，包括初始参数设置、优化速率或更新规则。例如：

MAML（Model-Agnostic Meta-Learning）：
- 学习一种通用的模型参数初始化，使得模型可以通过少量梯度更新快速适应新任务。
- 优点：能适应广泛的任务，并且与模型结构无关。
Reptile：
- 通过任务的随机采样和参数更新，寻找泛化能力强的初始模型。
LEO (Latent Embedding Optimization)：
- 在低维潜在空间中进行优化，减少高维特征的复杂性。

使用优化类方法时，模型的核心是利用元训练阶段学习到的初始化权重，使得它对于不同任务拥有更高的学习效率。

2. 基于记忆的元学习（Memory-Based Meta-Learning）

这种方法通过引入一个外部记忆单元（Memory Module），来存储任务相关信息或特征，帮助模型在训练过程中快速获取已有知识。例如：

Matching Networks：
- 将查询样本与支持集样本直接基于相似性进行匹配，通过记忆支持集实现分类。
Prototypical Networks：
- 每个类别通过支持集样本的特征均值生成一个“原型向量”，查询样本会根据其到原型向量的最近距离进行分类。
Memory-Augmented Neural Networks (MANN)：
- 神经网络采用可读写的记忆单元，用来存储和提取任务信息，帮助快速适应新的任务。

记忆增强方法非常适合小样本学习，因为它直接存储和复用已有任务的信息，大大减少了对训练样本的依赖。

3. 基于模型的元学习（Model-Based Meta-Learning）

这种方法通过训练一个模型，使其具备快速收敛的能力。例如：

RNN as Meta-Learner：
- 通过训练一个 RNN，将少量样本的任务信息以序列的方式输入，让 RNN 预测任务相关的参数更新。
SNAIL (Simple Neural Attentive Meta Learner)：
- 通过引入注意力机制的顺序建模，让模型更高效地学习如何从历史任务中快速学习规律。

模型类元学习方法强调结构化地建模任务，从而实现高效学习。

元学习的优势

快速适应性：
- 在新任务中，只需要少量样本就可以达到较好的效果，尤其在小样本场景下优势明显。
任务无关性：
- 尤其是基于优化的方法（如 MAML），能够在多种任务类型（分类、回归、强化学习）之间迁移。
更高效的学习过程：
- 基于记忆和模型的方法能够缩短模型的训练时间，同时提高性能。

元学习在开放世界小样本学习中的应用

根据上传的文档背景，元学习在开放世界小样本学习（Open-World Few-Shot Learning）中有以下重要应用：

应对分布变化：
- 在跨域小样本学习中，源域和目标域分布可能有显著差异。元学习能够通过任务分布上的训练，提高模型的泛化能力。
- 示例：使用优化类方法（如 MAML）可以让模型在跨域场景下快速适应目标任务。
处理未知类别：
- 在开放集场景下，元学习可以通过构建任务分布，增强模型对未知类别的检测能力。例如，Prototypical Networks 可以为每个类别找到清晰的特征分布，区分未知类和已知类。
噪声鲁棒性：
- 在含噪声样本的小样本学习中，记忆增强类方法（如 Matching Networks）通过直接存储支持集信息，在忽略噪声的同时优化分类性能。

研究挑战与未来方向

任务分布的挑战：
- 元学习假定任务之间存在共享规律，但在实际场景中，不同任务的分布可能大相径庭（例如跨域学习），如何设计鲁棒的任务抽样机制是一个方向。
开放世界的扩展：
- 在未知类别检测、动态类别增量学习等开放场景中的元学习仍存在较大难度，未来需要结合其他方法（如生成模型、对抗学习）来提升效果。
大规模训练的效率：
- 元学习由于需要在任务分布上训练，计算成本较高。未来方向包括低资源环境下的元学习、在线元学习等。

总结来看，元学习是一种适用于小样本、开放场景和任务分布复杂问题的通用方法论，也是开放世界小样本学习的重要支撑技术之一。它通过任务间的知识共享与快速适应能力，为各种复杂场景的模型泛化提供了强有力的技术方案。

posted @ 2025-04-10 18:04 bonelee 阅读(240) 评论(0) 收藏举报

刷新页面返回顶部

将者，智、信、仁、勇、严也。

Hi，我是李智华，华为-安全AI算法专家，欢迎来到安全攻防对抗的有趣世界。