二分查找 难题汇总 模板验证 二分答案 本质上是答案在一段range里,然后根据该range去二分搜索!
69. x 的平方根 二分答案的雏形
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
class Solution:
def mySqrt(self, x: int) -> int:
if x == 0:
return x
l, r = 1, x//2 + 1
while l + 1 < r:
mid = (l + r) // 2
if mid * mid <= x:
l = mid
else:
r = mid
return l
29. 两数相除
给你两个整数,被除数 dividend 和除数 divisor。将两数相除,要求 不使用 乘法、除法和取余运算。
整数除法应该向零截断,也就是截去(truncate)其小数部分。例如,8.345 将被截断为 8 ,-2.7335 将被截断至 -2 。
返回被除数 dividend 除以除数 divisor 得到的 商 。
注意:假设我们的环境只能存储 32 位 有符号整数,其数值范围是 [−231, 231 − 1] 。本题中,如果商 严格大于 231 − 1 ,则返回 231 − 1 ;如果商 严格小于 -231 ,则返回 -231 。
示例 1:
输入: dividend = 10, divisor = 3 输出: 3 解释: 10/3 = 3.33333.. ,向零截断后得到 3 。
示例 2:
输入: dividend = 7, divisor = -3 输出: -2 解释: 7/-3 = -2.33333.. ,向零截断后得到 -2 。
提示:
-231 <= dividend, divisor <= 231 - 1divisor != 0
leetcode上的,一开始都没有反应过来要用二分答案。
def quick_mul(x,y):
ans = 0
while y:
if y & 1:
ans += x
x += x
y >>= 1
return ans
class Solution:
def divide(self, dividend: int, divisor: int) -> int:
def helper(a, b):
a, b = abs(a), abs(b)
if a < b:
return 0
l, r = 1, a
while l + 1 < r:
mid = (l + r) // 2
if quick_mul(b, mid) <= a:
l = mid
else:
r = mid
if quick_mul(l, b) == a:
return l
if quick_mul(r, b) == a:
return r
return l
if dividend > 0 and divisor < 0:
ans = -helper(dividend, divisor)
elif dividend < 0 and divisor > 0:
ans = -helper(dividend, divisor)
else:
ans = helper(dividend, divisor)
min_val, max_val = -(1<<31), (1<<31)-1
if ans > max_val:
ans = max_val
if ans < min_val:
ans = min_val
return ans
4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2] 输出:2.00000 解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4] 输出:2.50000 解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
经典题目:见我另外文章分析思路
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
def findKth(A, l_a, r_a, B, l_b, r_b, k):
rangeA = r_a - l_a + 1
rangeB = r_b - l_b + 1
if rangeA == 0:
return B[l_b+k-1]
if rangeB == 0:
return A[l_a+k-1]
if k == 1: # 注意位置,是放在上面2个if后面,k为1时,只需要返回A B首个元素最小即可
return min(A[l_a], B[l_b])
if rangeA > rangeB: # 之所有要交换,是因为后面pb = k - pa可能导致l_b + pb越界!例如:A有100个元素,B只有1个,k为50的情形
return findKth(B, l_b, r_b, A, l_a, r_a, k)
pa = min(k // 2, rangeA)
pb = k - pa
if A[l_a + pa - 1] == B[l_b + pb - 1]:
return A[l_a + pa - 1]
elif A[l_a + pa - 1] < B[l_b + pb - 1]:
return findKth(A, l_a + pa, r_a, B, l_b, l_b + pb - 1, k - pa) # 注意收缩r_b为l_b + pb - 1, 这是因为我们已经知道 A[l_a + pa - 1] 小于 B[l_b + pb - 1],并且 pa + pb = k。这意味着在 A 和 B 的合并数组中,B[l_b + pb - 1] 前面至少有 k 个元素(包括 B[l_b + pb - 1] 本身)。因此,第 k 大的元素不可能在 B[l_b + pb - 1] 之后。
else:
return findKth(A, l_a, l_a + pa - 1, B, l_b + pb, r_b, k - pb)
A, B = nums1, nums2
k = len(A) + len(B)
if k & 1:
return findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2 + 1) # 注意有+1,因为是第k大
else:
a = findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2 + 1) # 注意有+1,因为是第k大
b = findKth(A, 0, len(A) - 1, B, 0, len(B) - 1, k//2)
return (a + b)/2
75 · 寻找峰值
给定一个整数数组(size为n),其具有以下特点:
- 相邻位置的数字是不同的
A[0] < A[1]并且A[n - 2] > A[n - 1]
假定P是峰值的位置则满足A[P] > A[P-1]且A[P] > A[P+1],返回数组中任意一个峰值的位置。
- 数组保证至少存在一个峰
- 如果数组存在多个峰,返回其中任意一个就行
- 数组至少包含 3 个数
样例 1:
输入:
A = [1, 2, 1, 3, 4, 5, 7, 6]输出:
1解释:
返回任意一个峰顶元素的下标,6也同样正确。
样例 2:
输入:
A = [1,2,3,4,1]输出:
3解释:
返回峰顶元素的下标。
https://www.lintcode.com/problem/75/
分析:

注意:a[mid-1] a[mid] a[mid+1]一定不会越界!!!
from typing import (
List,
)
class Solution:
"""
@param a: An integers array.
@return: return any of peek positions.
"""
def find_peak(self, a: List[int]) -> int:
# write your code here
l, r = 0, len(a) - 1
while l + 1 < r:
mid = (l + r) // 2
if a[mid] <= a[mid+1]:
l = mid
else:
r = mid
if a[l] >= a[r]:
return l
return r
141. 对x开根
实现 int sqrt(int x) 函数,计算并返回 x 的平方根。
样例
Example 1:
Input: 0
Output: 0
Example 2:
Input: 3
Output: 1
Explanation:
return the largest integer y that y*y <= x.
Example 3:
Input: 4
Output: 2
挑战
O(log(x))
class Solution:
"""
@param x: An integer
@return: The sqrt of x
"""
def sqrt(self, x):
# write your code here
l, r = 0, x
while l + 1 < r:
mid = (l + r) >> 1
if mid*mid > x:
r = mid
else:
l = mid
if r*r == x:
return r
return l
https://www.lintcode.com/problem/141/
class Solution:
"""
@param x: An integer
@return: The sqrt of x
"""
def sqrt(self, x: int) -> int:
# write your code here
assert x >= 0
if x <= 1:
return x
l, r = 0, x - 1
while l + 1 < r:
mid = (l + r) // 2
if mid * mid <= x:
l = mid
else:
r = mid
if l * l <= x:
return l
return r
183. 木材加工
有一些原木,现在想把这些木头切割成一些长度相同的小段木头,需要得到的小段的数目至少为 k。当然,我们希望得到的小段越长越好,你需要计算能够得到的小段木头的最大长度。
样例
Example 1
Input:
L = [232, 124, 456]
k = 7
Output: 114
Explanation: We can cut it into 7 pieces if any piece is 114cm long, however we can't cut it into 7 pieces if any piece is 115cm long.
Example 2
Input:
L = [1, 2, 3]
k = 7
Output: 0
Explanation: It is obvious we can't make it.
挑战
O(n log Len), Len为 n 段原木中最大的长度
注意事项
木头长度的单位是厘米。原木的长度都是正整数,我们要求切割得到的小段木头的长度也要求是整数。无法切出要求至少 k 段的,则返回 0 即可。
木头长度的范围在 1 到 max(L),在这个范围内二分出一个长度 length,然后看看以这个 wood length 为前提的基础上,能切割出多少木头,如果少于 k 根,说明要短一些才行,如果多余 k,说明可以继续边长一些。
L = [232, 124, 456] k = 7 Output: 114
为啥是114因为(232/114 == 2)+(123/114==1) + (456/114==4) == 7
如果长度继续延长,例如115,则(232/115 == 2)+(123/115==1) + (456/115==3) == 6 所以k=7满足不了!
如果长度减少,极端情况是1,则(232/1 == 232)+(123/1==123) + (456/1==456) > 7 。。。
所以本质上是二分。。。
https://www.lintcode.com/problem/183/
class Solution:
"""
@param L: Given n pieces of wood with length L[i]
@param k: An integer
@return: The maximum length of the small pieces
"""
def woodCut(self, L, k):
# write your code here
def cut_piece(length):
ans = 0
for i in L:
ans += i // length
return ans
if not L:
return 0
l, r = 1, max(L)
while l + 1 < r:
mid = (l + r) >> 1
if cut_piece(mid) >= k:
l = mid
else:
r = mid
if cut_piece(r) >= k:
return r
if cut_piece(l) >= k:
return l
return 0
看到了吧,其实二分答案的模板还是很简单的,就是二分的模板!!!
437. 书籍复印
给定 n 本书, 第 i 本书的页数为 pages[i]. 现在有 k 个人来复印这些书籍, 而每个人只能复印编号连续的一段的书, 比如一个人可以复印 pages[0], pages[1], pages[2], 但是不可以只复印 pages[0], pages[2], pages[3] 而不复印 pages[1].
所有人复印的速度是一样的, 复印一页需要花费一分钟, 并且所有人同时开始复印. 怎样分配这 k 个人的任务, 使得这 n 本书能够被尽快复印完?
返回完成复印任务最少需要的分钟数.
样例
样例 1:
输入: pages = [3, 2, 4], k = 2
输出: 5
解释: 第一个人复印前两本书, 耗时 5 分钟. 第二个人复印第三本书, 耗时 4 分钟.
样例 2:
输入: pages = [3, 2, 4], k = 3
输出: 4
解释: 三个人各复印一本书.
挑战
时间复杂度 O(nk)
注意事项
书籍页数总和小于等于2147483647
基于答案值域的二分法。 答案的范围在 max(pages)~sum(pages) 之间,每次二分到一个时间 time_limit 的时候,用贪心法从左到右扫描一下 pages,看看需要多少个人来完成抄袭。 如果这个值 <= k,那么意味着大家花的时间可能可以再少一些,如果 > k 则意味着人数不够,需要降低工作量。
时间复杂度 O(nlog(sum)) ==>不太容易想到。。。还是非常巧妙的!
https://www.lintcode.com/problem/437/
是该问题时间复杂度上的最优解法
class Solution:
"""
@param pages: an array of integers
@param k: An integer
@return: an integer
"""
def copyBooks(self, pages, k):
if not pages:
return 0
start, end = max(pages), sum(pages)
while start + 1 < end:
mid = (start + end) // 2
if self.get_least_people(pages, mid) <= k:
end = mid
else:
start = mid
if self.get_least_people(pages, start) <= k:
return start
return end
def get_least_people(self, pages, time_limit):
count = 0
time_cost = 0
for page in pages:
if time_cost + page > time_limit:
count += 1
time_cost = 0
time_cost += page
return count + 1
from typing import (
List,
)
class Solution:
"""
@param pages: an array of integers
@param k: An integer
@return: an integer
"""
def copy_books(self, pages: List[int], k: int) -> int:
# write your code here
assert k > 0
if not pages:
return 0
l, r = max(pages), sum(pages)
while l + 1 < r:
mid = (l + r) // 2
num = self.need_least_people(pages, mid)
if num > k:
l = mid
else:
r = mid
if self.need_least_people(pages, l) <= k:
return l
return r
def need_least_people(self, pages, n):
ans = 0
s = 0
i = 0
while i < len(pages):
while i < len(pages) and s + pages[i] <= n:
s += pages[i]
i += 1
s = 0
ans += 1
return ans
633. 寻找重复的数
给出一个数组 nums 包含 n + 1 个整数,每个整数是从 1 到 n (包括边界),保证至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
样例
Example 1:
Input:
[5,5,4,3,2,1]
Output:
5
Example 2:
Input:
[5,4,4,3,2,1]
Output:
4
注意事项
1.不能修改数组(假设数组只能读)
2.只能用额外的O(1)的空间
3.时间复杂度小于O(n^2)
4.数组中只有一个重复的数,但可能重复超过一次
- x轴是 0, 1, 2, ... n。
- y轴是对应的 <=x 的数的个数,比如 <=0 的数的个数是0,就在(0,0)这个坐标画一个点。<=n 的数的个数是 n+1 个,就在 (n,n+1)画一个点。
把所有的点连接起来之后,是一个类似下图的折线:
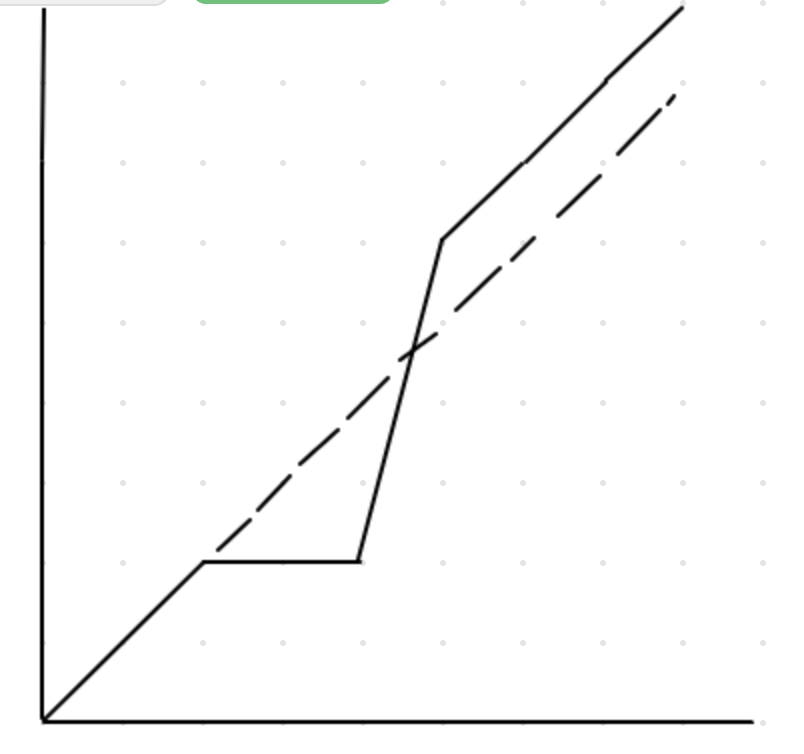
我们可以知道这个折线图的有如下的一些属性:
- 大部分时候,我们会沿着斜率为 1 的那条虚线前进
- 如果出现了一些空缺的数,就会有横向的折线
- 一旦出现了重复的数,就会出现一段斜率超过 1 的折线
- 斜率超过 1 的折线只会出现一次
试想一下,对比 y=x 这条虚线,当折线冒过了这条虚线出现在这条虚线的上方的时候,一定是遇到了一个重复的数。 一旦越过了这条虚线以后,就再也不会掉到虚线的下方或者和虚线重叠。 因为折线最终会停在 (n,n+1) 这个位置,如果要从 y=x 这条虚线或者这条虚线的下方到达 (n,n+1) 这个位置, 一定需要一个斜率 > 1的折线段,而这个与题目所说的重复的数只有一个就是矛盾的。因此可以证明,斜率超过1 的折线只会出现1次, 且会将折线整体带上 y=x 这条虚线的上方。因此第一个在 y=x 上方的 x 点,就是我们要找的重复的数。
时间复杂度是 O(nlogn)
public class Solution {
/**
* @param nums an array containing n + 1 integers which is between 1 and n
* @return the duplicate one
*/
public int findDuplicate(int[] nums) {
// Write your code here
int l = 1;
int r = nums.length - 1; // n
while (l + 1 < r) {
int mid = l + (r - l) / 2;
if (count(nums, mid) <= mid) {
l = mid;
} else {
r = mid;
}
}
if (count(nums, l) <= l) {
return r;
}
return l;
}
private int count(int[] nums, int mid) {
int cnt = 0;
for (int item : nums) {
if (item <= mid) {
cnt++;
}
}
return cnt;
}
}
from typing import (
List,
)
class Solution:
"""
@param nums: an array containing n + 1 integers which is between 1 and n
@return: the duplicate one
"""
def find_duplicate(self, nums: List[int]) -> int:
# write your code here
l, r = 1, len(nums) - 1
while l + 1 < r:
mid = (l + r) // 2
if self.count_lessthan(nums, mid) <= mid:
l = mid
else:
r = mid
if self.count_lessthan(nums, l) <= l:
return r
return l
def count_lessthan(self, nums, n):
return sum(1 for i in nums if i <= n)
利用分值二分法來計算出答案。
答案的範圍會在start, end = 1, max(nums)之間,去計算小於等於mid的個數617. 子数组的最大平均值 II
给出一个整数数组,有正有负。找到这样一个子数组,他的长度大于等于 k,且平均值最大。
样例
Example 1:
Input:
[1,12,-5,-6,50,3]
3
Output:
15.667
Explanation:
(-6 + 50 + 3) / 3 = 15.667
Example 2:
Input:
[5]
1
Output:
5.000
注意事项
保证数组的大小 >= k
基于二分答案的方法 二分出 average 之后,把数组中的每个数都减去 average,然后的任务就是去求这个数组中,是否有长度 >= k 的 subarray,他的和超过 0。==>解法不优雅!感觉还不如传统解决N^2前缀和解法!
class Solution:
"""
@param: nums: an array with positive and negative numbers
@param: k: an integer
@return: the maximum average
"""
def maxAverage(self, nums, k):
if not nums:
return 0
start, end = min(nums), max(nums)
while end - start > 1e-5:
mid = (start + end) / 2
if self.check_subarray(nums, k, mid):
start = mid
else:
end = mid
return start
def check_subarray(self, nums, k, average):
prefix_sum = [0]
for num in nums:
prefix_sum.append(prefix_sum[-1] + num - average)
min_prefix_sum = 0
for i in range(k, len(nums) + 1):
if prefix_sum[i] - min_prefix_sum >= 0:
return True
min_prefix_sum = min(min_prefix_sum, prefix_sum[i - k + 1])
return False我们再来一个结合贪心的二分搜索(当然,用dp更直观)
nums ,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
输入:nums = [10,9,2,5,3,7,101,18] 输出:4 解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
输入:nums = [0,1,0,3,2,3] 输出:4
示例 3:
输入:nums = [7,7,7,7,7,7,7] 输出:1
import bisect
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
"""
如果使用二分查找算法,我们可以维护一个数组tails,其中tails[i]是长度为i+1的所有递增子序列中末尾元素的最小值。对于每个元素nums[i],我们可以使用二分查找在tails中找到第一个大于nums[i]的元素,并用nums[i]替换它。如果nums[i]大于tails中的所有元素,那么我们就将nums[i]添加到tails的末尾。最后,tails的长度就是最长递增子序列的长度。
见https://leetcode.cn/problems/longest-increasing-subsequence/solutions/24173/zui-chang-shang-sheng-zi-xu-lie-dong-tai-gui-hua-2/?company_slug=bytedance 本质上是贪心
"""
tails = []
for num in nums:
index = bisect.bisect_left(tails, num)
if index == len(tails):
tails.append(num)
else:
tails[index] = num
return len(tails)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号