LSTM如何解决梯度消失或爆炸的？

from:https://zhuanlan.zhihu.com/p/44163528

哪些问题？

  • 梯度消失会导致我们的神经网络中前面层的网络权重无法得到更新，也就停止了学习。
  • 梯度爆炸会使得学习不稳定， 参数变化太大导致无法获取最优参数。
  • 在深度多层感知机网络中，梯度爆炸会导致网络不稳定，最好的结果是无法从训练数据中学习，最坏的结果是由于权重值为NaN而无法更新权重。
  • 在循环神经网络（RNN）中，梯度爆炸会导致网络不稳定，使得网络无法从训练数据中得到很好的学习，最好的结果是网络不能在长输入数据序列上学习。

3. 原因何在？

让我们以一个很简单的例子分析一下，这样便于理解。

 

 

如上图，是一个每层只有一个神经元的神经网络，且每一层的激活函数为sigmoid，则有：

y_i = \sigma(z_i) = \sigma(w_ix_i + b_i)  ( \sigma 是sigmoid函数)。

我们根据反向传播算法有：

\frac{\delta C}{\delta b_1} = \frac{\delta C}{ \delta y_4} \frac{\delta y_4}{\delta z_4} \frac{\delta z_4}{\delta x_4} \frac{ \delta x_4}{\delta z_3} \frac{\delta z_3}{ \delta x_3} \frac{ \delta x_3}{\delta z_2} \frac{\delta z_2}{ \delta x_2} \frac{ \delta x_2}{\delta z_1} \frac{\delta z_1}{\delta b_1} \\ = \frac{ \delta C}{\delta y_4} （\sigma '(z_4) w_4）（ \sigma'(z_3) w_3）（ \sigma ' (z_2) w_2）（ \sigma ' (z_1)）

而sigmoid函数的导数公式为：  S'(x ) = \frac{e^{-x}}{(1+ e^{-x})^2} = S(x)(1- S(x))  它的图形曲线为：

 

 

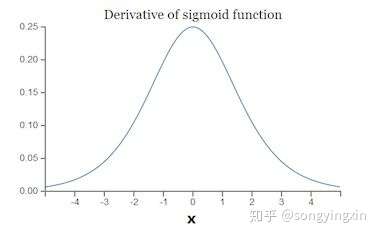
由上可见，sigmoid函数的导数 \sigma'(x) 的最大值为 \frac{1}{4} ，通常我们会将权重初始值 |w| 初始化为为小于1的随机值，因此我们可以得到 |\sigma '(z_4) w_4| < \frac{1}{4} ，随着层数的增多，那么求导结果\frac{\delta C}{\delta b_1} 越小，这也就导致了梯度消失问题。

那么如果我们设置初始权重 |w| 较大，那么会有 |\sigma '(z_4) w_4| > 1  ，造成梯度太大（也就是下降的步伐太大），这也是造成梯度爆炸的原因。

总之，无论是梯度消失还是梯度爆炸，都是源于网络结构太深，造成网络权重不稳定，从本质上来讲是因为梯度反向传播中的连乘效应。

4. RNN中的梯度消失，爆炸问题

参考：RNN梯度消失和爆炸的原因， 这篇文章是我看到讲的最清楚的了，在这里添加一些我的思考， 若侵立删。

我们给定一个三个时间的RNN单元，如下：

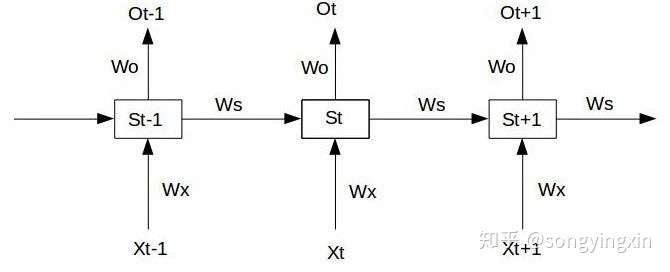
我们假设最左端的输入 S_0 为给定值， 且神经元中没有激活函数（便于分析）， 则前向过程如下：

S_1 = W_xX_1 + W_sS_0 + b_1 \qquad \qquad \qquad O_1 = W_oS_1 + b_2 \\ S_2 = W_xX_2 + W_sS_1 + b_1 \qquad \qquad \qquad O_2 = W_oS_2 + b_2 \\ S_3 = W_xX_3 + W_sS_2 + b_1 \qquad \qquad \qquad O_3 = W_oS_3 + b_2 \\

在 t=3 时刻， 损失函数为 L_3 = \frac{1}{2}(Y_3 - O_3)^2 ，那么如果我们要训练RNN时， 实际上就是是对 W_x, W_s, W_o,b_1,b_2 求偏导， 并不断调整它们以使得 L_3 尽可能达到最小（参见反向传播算法与梯度下降算法)。

那么我们得到以下公式：

\frac{\delta L_3}{\delta W_0} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta W_0} \\ \frac{\delta L_3}{\delta W_x} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_x} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_x} \\ \frac{\delta L_3}{\delta W_s} = \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta W_s} + \frac{\delta L_3}{\delta O_3} \frac{\delta O_3}{\delta S_3} \frac{\delta S_3}{\delta S_2} \frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_s} \\

将上述偏导公式与第三节中的公式比较，我们发现， 随着神经网络层数的加深对 W_0 而言并没有什么影响， 而对 W_x, W_s 会随着时间序列的拉长而产生梯度消失和梯度爆炸问题。

根据上述分析整理一下公式可得， 对于任意时刻t对 W_x, W_s 求偏导的公式为：

\frac{\delta L_t}{\delta W_x } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_x} \\ \frac{\delta L_t}{\delta W_s } = \sum_{k=0}^t \frac{\delta L_t}{\delta O_t} \frac{\delta O_t}{\delta S_t}( \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ) \frac{ \delta S_k }{\delta W_s}

我们发现， 导致梯度消失和爆炸的就在于 \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} ， 而加上激活函数后的S的表达式为：

S_j = tanh(W_xX_j + W_sS_{j-1} + b_1)

那么则有：

\prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}} = \prod_{j=k+1}^t tanh' W_s

而在这个公式中， tanh的导数总是小于1 的， 如果 W_s 也是一个大于0小于1的值， 那么随着t的增大， 上述公式的值越来越趋近于0， 这就导致了梯度消失问题。 那么如果 W_s 很大， 上述公式会越来越趋向于无穷， 这就产生了梯度爆炸。

5. 为什么LSTM能解决梯度问题？

在阅读此篇文章之前，确保自己对LSTM的三门机制有一定了解， 参见：LSTM：RNN最常用的变体

从上述中我们知道， RNN产生梯度消失与梯度爆炸的原因就在于 \prod_{j=k+1}^t \frac{\delta S_j}{\delta S_{j-1}}  ， 如果我们能够将这一坨东西去掉， 我们的不就解决掉梯度问题了吗。 LSTM通过门机制来解决了这个问题。

我们先从LSTM的三个门公式出发：

  • 遗忘门： f_t = \sigma( W_f \cdot [h_{t-1}, x_t] + b_f)
  • 输入门： i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)
  • 输出门： o_t = \sigma(W_o \cdot [h_{t-1}, x_t ] + b_0 )
  • 当前单元状态 c_t : c_t = f_t \circ c_{t-1} + i_t \circ tanh(W_c \cdot [h_{t-1}, x_t] + b_c )
  • 当前时刻的隐层输出： h_t = o_t \circ tanh(c_t)

我们注意到， 首先三个门的激活函数是sigmoid， 这也就意味着这三个门的输出要么接近于0 ， 要么接近于1。这就使得 \frac{\delta c_t}{\delta c_{t-1}} = f_t， \frac{\delta h_t}{\delta h_{t-1}} = o_t 是非0即1的，当门为1时， 梯度能够很好的在LSTM中传递，很大程度上减轻了梯度消失发生的概率， 当门为0时，说明上一时刻的信息对当前时刻没有影响， 我们也就没有必要传递梯度回去来更新参数了。所以， 这就是为什么通过门机制就能够解决梯度的原因： 使得单元间的传递 \frac{\delta S_j}{\delta S_{j-1}} 为0 或 1。

 

https://blog.csdn.net/hx14301009/article/details/80401227  里提到还有CEC。

 

则梯度会随着反向传播层数的增加而呈指数增长，导致梯度爆炸。

如果对于所有的 有

则在经过多层的传播后，梯度会趋向于0，导致梯度弥散（消失）。

Sepp Hochreiter 和 Jürgen Schmidhuber 在他们提出 Long Short Term Memory 的文章里讲到，为了避免梯度弥散和梯度爆炸，一个 naive 的方法就是强行让 error flow 变成一个常数：


就是RNN里自己到自己的连接。他们把这样得到的模块叫做CEC（constant error carrousel），很显然由于上面那个约束条件的存在，这个CEC模块是线性的。这就是LSTM处理梯度消失的问题的动机。

通俗地讲：RNN中，每个记忆单元h_t-1都会乘上一个W和激活函数的导数，这种连乘使得记忆衰减的很快，而LSTM是通过记忆和当前输入"相加"，使得之前的记忆会继续存在而不是受到乘法的影响而部分“消失”，因此不会衰减。但是这种naive的做法太直白了，实际上就是个线性模型，在学习效果上不够好，因此LSTM引入了那3个门：

作者说所有“gradient based”的方法在权重更新都会遇到两个问题：

input weight conflict 和 output weight conflict

大意就是对于神经元的权重 ，不同的数据 所带来的更新是不同的，这样可能会引起冲突（比如有些输入想让权重变小，有些想让它变大）。网络可能需要选择性地“忘记”某些输入，以及“屏蔽”某些输出以免影响下一层的权重更新。为了解决这些问题就提出了“门”。

举个例子：在英文短语中，主语对谓语的状态具有影响，而如果之前同时出现过第一人称和第三人称，那么这两个记忆对当前谓语就会有不同的影响，为了避免这种矛盾，我们希望网络可以忘记一些记忆来屏蔽某些不需要的影响。

因为LSTM对记忆的操作是相加的，线性的，使得不同时序的记忆对当前的影响相同，为了让不同时序的记忆对当前影响变得可控，LSTM引入了输入门和输出门，之后又有人对LSTM进行了扩展，引入了遗忘门。

总结一下：LSTM把原本RNN的单元改造成一个叫做CEC的部件，这个部件保证了误差将以常数的形式在网络中流动 ，并在此基础上添加输入门和输出门使得模型变成非线性的，并可以调整不同时序的输出对模型后续动作的影响。



 

posted @ 2019-03-05 11:08  bonelee  阅读(39536)  评论(1)  编辑  收藏  举报