04.深度学习--反向传播
深度学习--反向传播
Backpropagation反向传播
传统的梯度下降的方法,是将所有的参数写在一个θ向量里面,在这个向量里面的参数分别求偏导数,之后再对θ向量进行更新。但是如果在神经网络中,会有很多层,每一层对应也会有很多个参数,于是会让θ向量变得非常长,而我们要做的是如何有效的将这个百万维的参数向量计算出来,而这个就是反向传播在做的事情,他并不是一个和梯度下降不同的计算的方法,他就是梯度下降的方法,只是效率较高,可以更加有效率的把梯度下降需要变化的变量计算出来

Chain Rule链式法则
链式法则主要分为两种情况,是在对某个变量进行求导时可以通过中间变量进行求导。
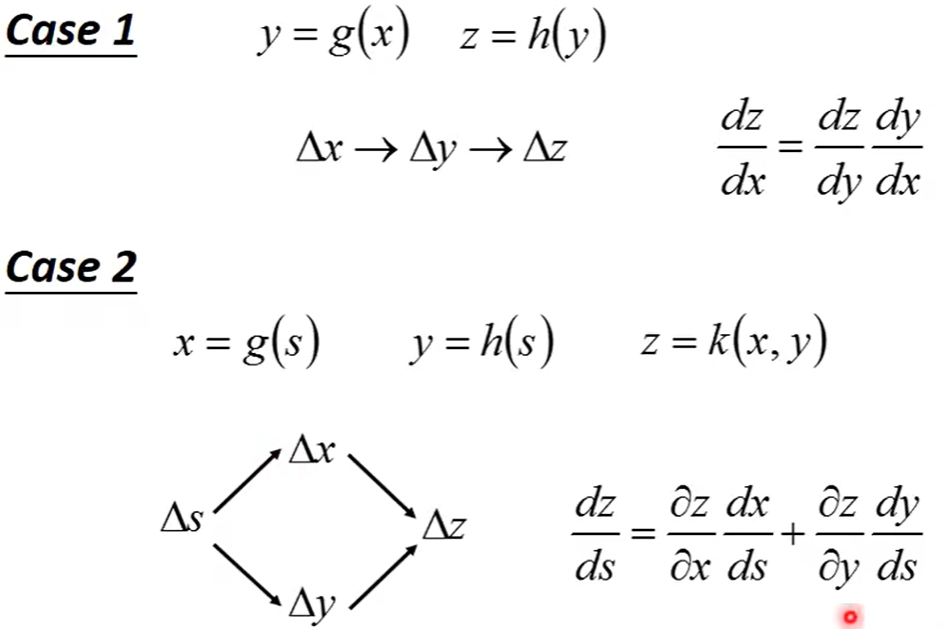
回到我们的反向传播中去,当我们定义了一个loss函数,这个loss函数中的Cn表示给出的预测值和真实值之间的差距,当我们将所有的训练集的数据的Cn进行相加,就可以的得到loss函数,当对loss函数求关于w的偏微分时,可以得到右边式子,至此不需要进行loss函数对w的求导,只需要对一组数据的Cn进行w的求导就可以将所有的相加最后得到Loss函数对w的求导
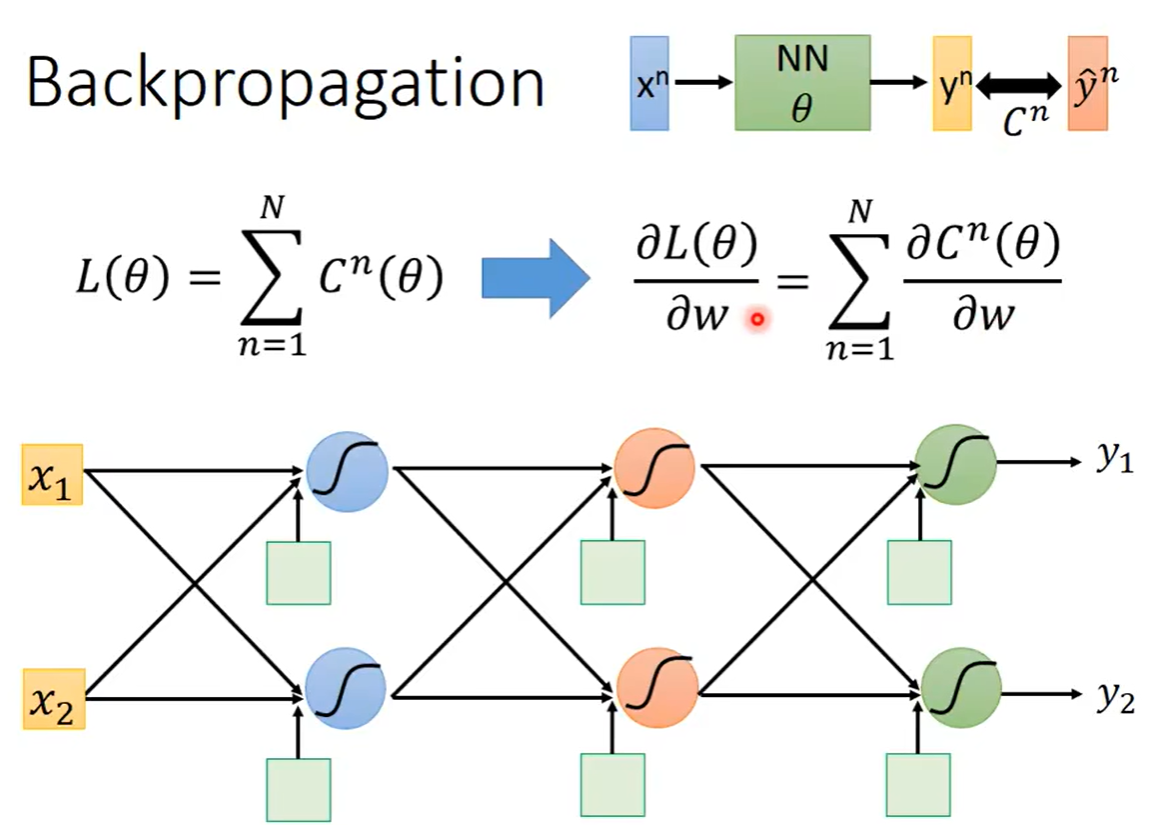
我们首先考虑某一个神经元,首先取第一层的一个神经元,当计算C中对z的偏导数的时候,我们首先考虑加入中间变量z,也就是C对z求导,再乘上z对w求导
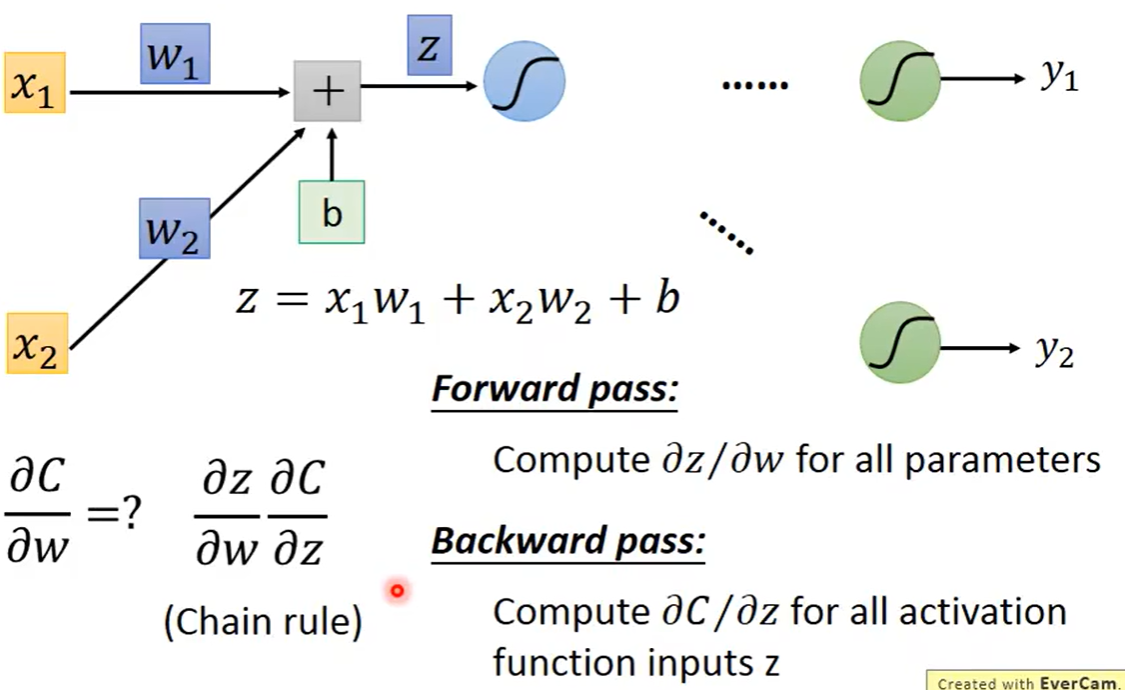
我们可以很轻易地将z对w的求导算出,导数结果就是权重w乘的数据x,也就是w对应的input是什么求导结果就是什么,w1对应x1,w2对应x2

较难的部分是C关于z的偏导数,假设通过这神经元得到的结果是a,之后这个a又乘上相应的权重,加上其他input乘以权重之后又得到了一个新的结果,此时C关于z的偏导数又可以进一步拆解
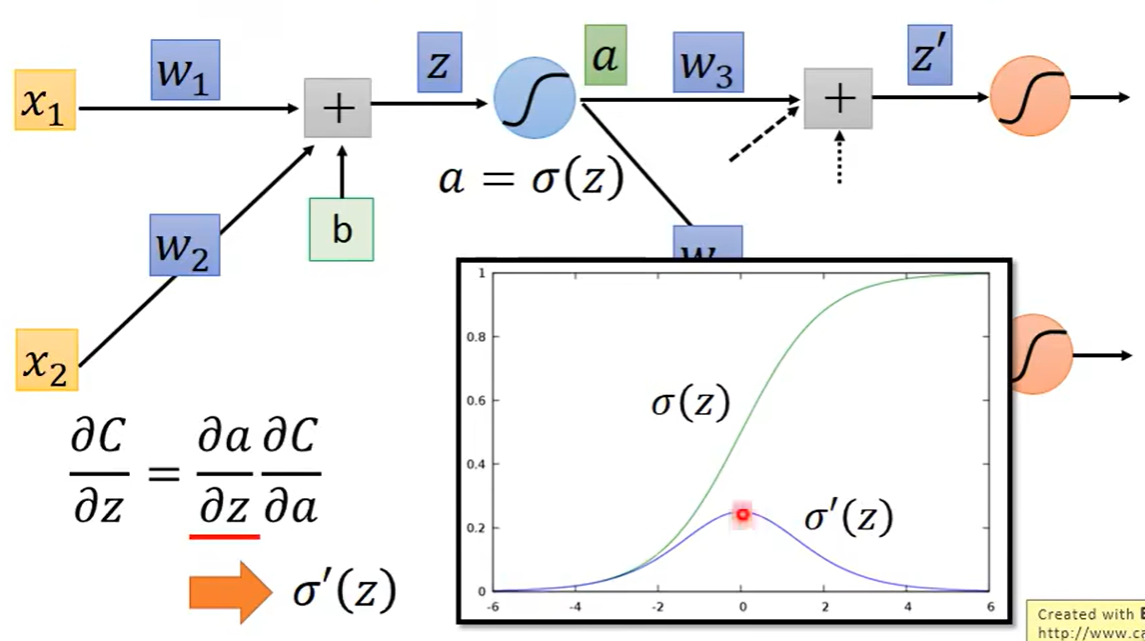
此时问题就是对C关于a求解偏导数,分解之后就是a作为多少个神经元的input那么就会有多少个新的偏导数进行相加
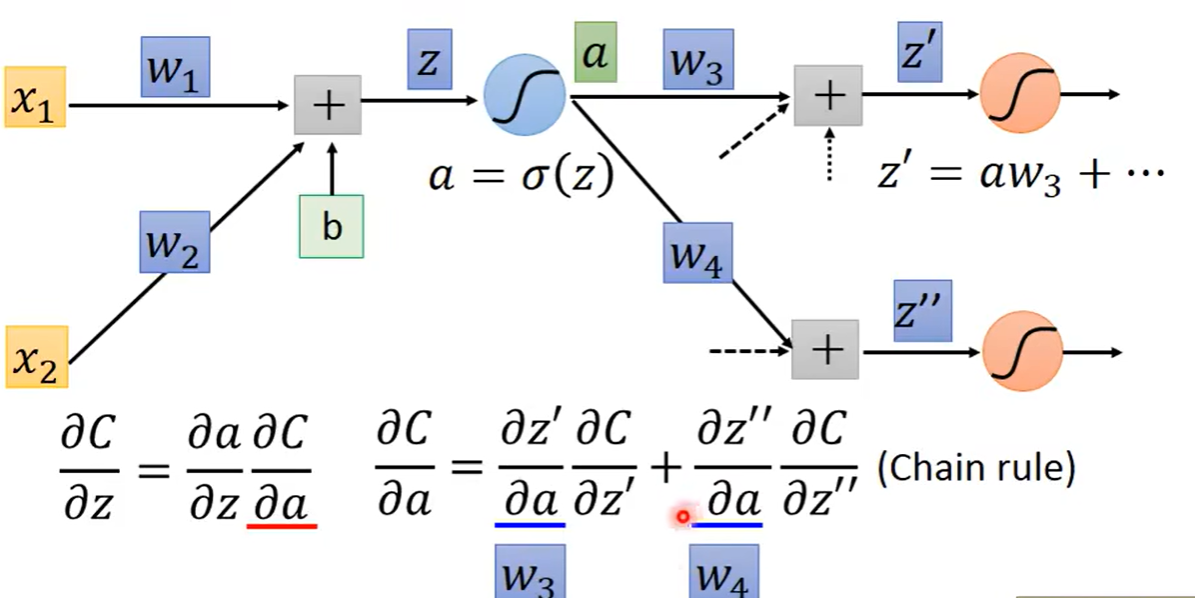
假设我们此时已经算出来了C关于z`和z``的偏导数,那么此时C关于z的偏导数便可得出结果,是由上两图综合计算出
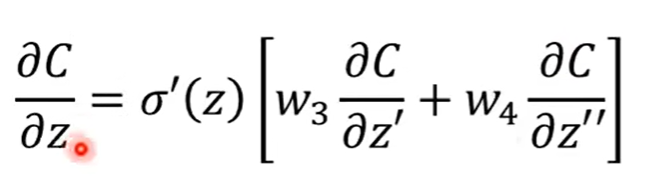
所以可以倒过来推到得到我们想要计算的偏导数,假设有一个神经元,我们可以倒着通过偏导数乘以相应的weight得到这个神经元前一个神经元需要的偏导数
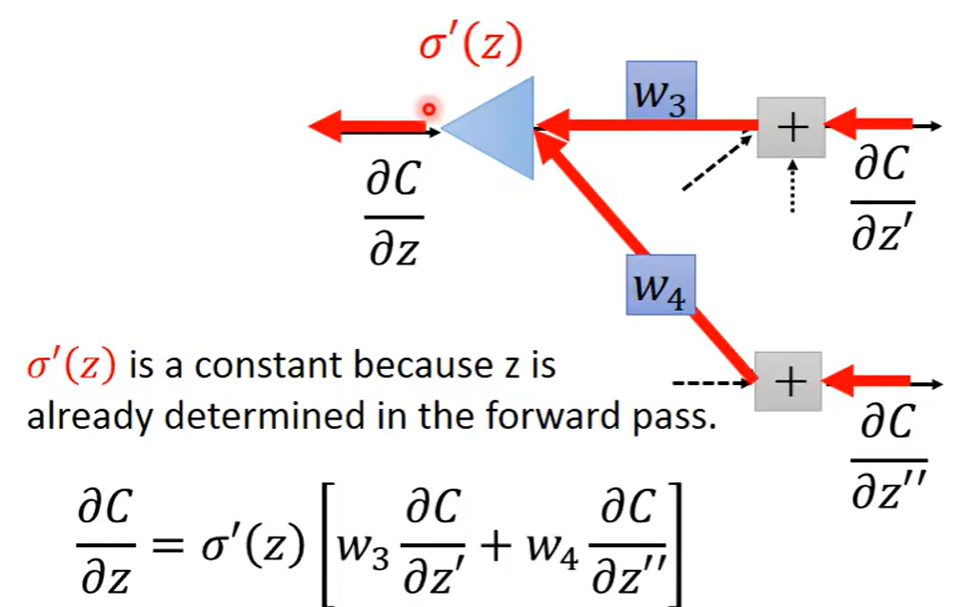
最后就分为两种情况
-
第一种是我们上图中z`后面的就是output
此时只需要轻易的计算两个偏导数便可得出最后结论,最后通过反向传播的方式反过来计算就可以得出想要的C关于w的偏导数
![]()
-
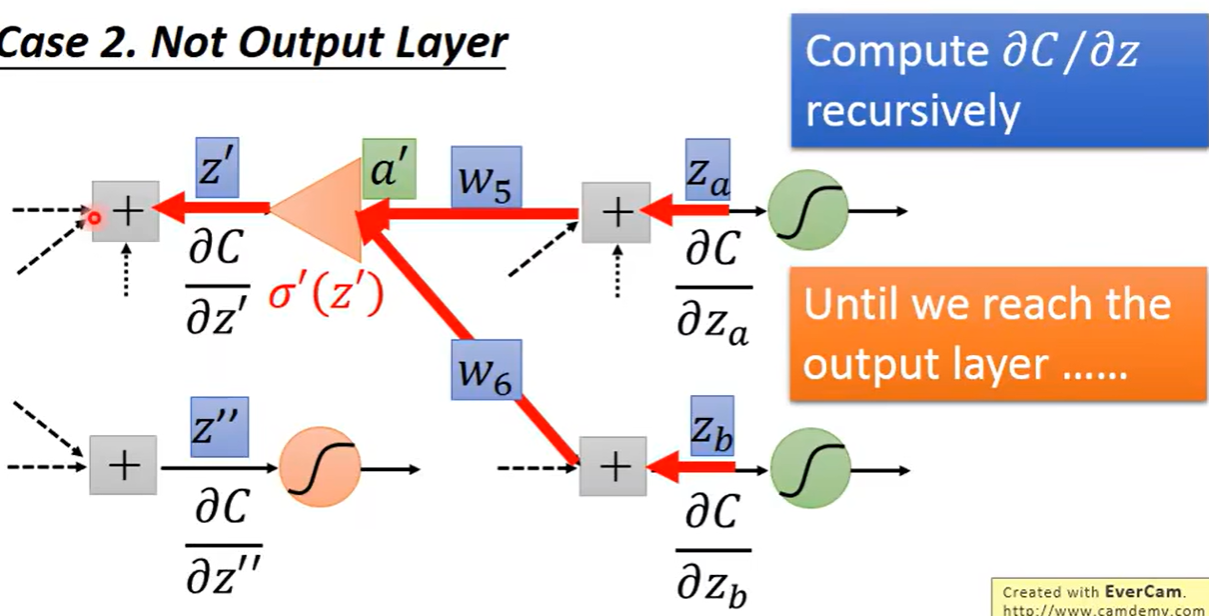
第二种是此时的z`并非最后一层,可以直接利用反向传播直接计算
![]()
总结


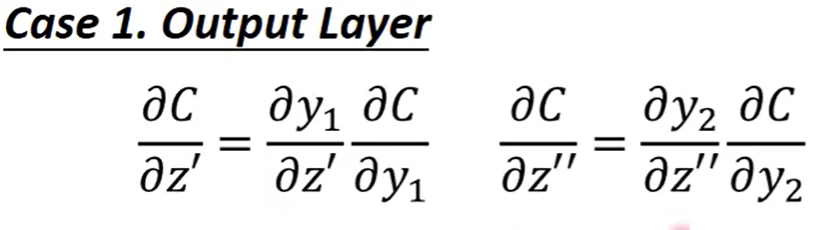

 浙公网安备 33010602011771号
浙公网安备 33010602011771号