FFT算法详解

DFT

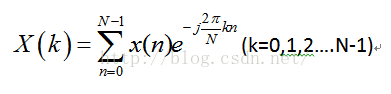
DIT-FFT (Decimation in time) Base-2

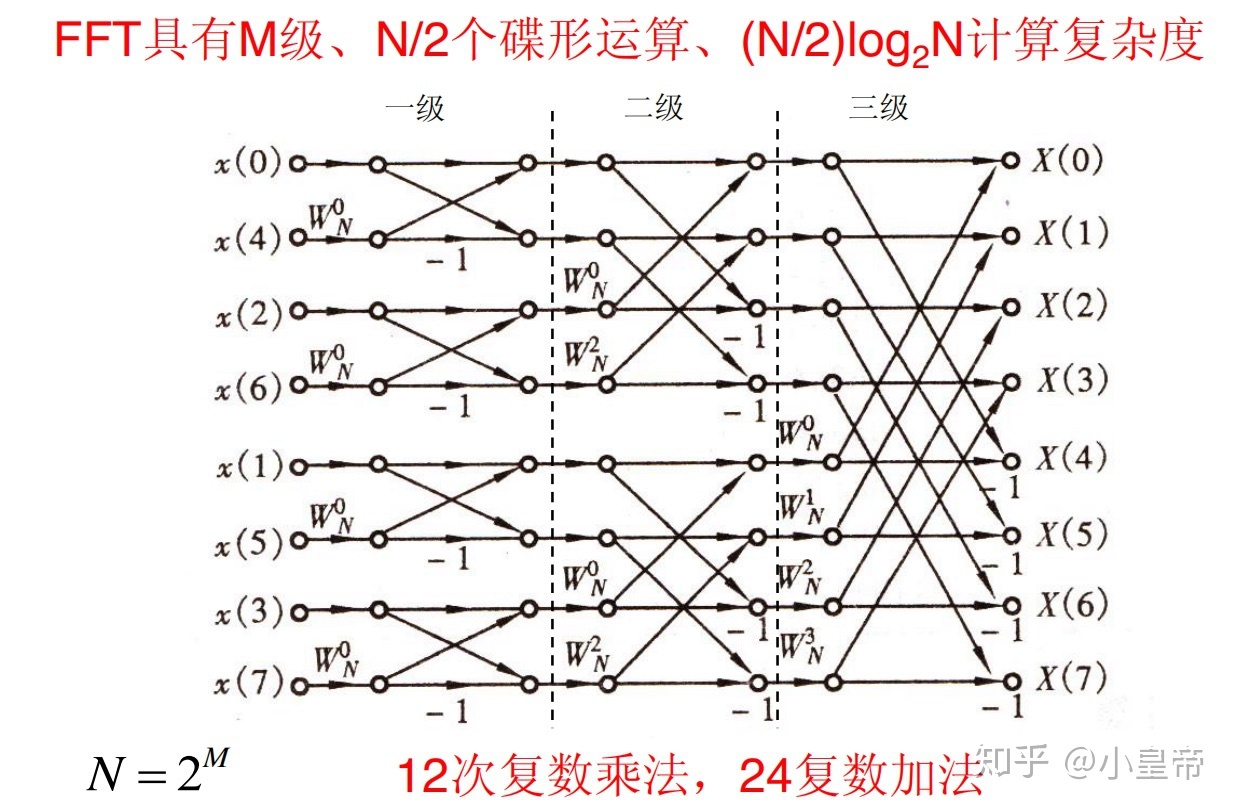
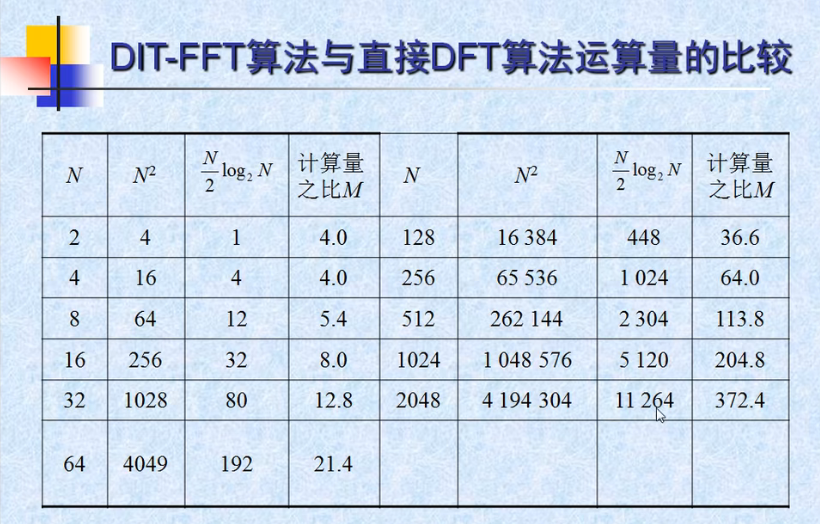
python code：

def CalcDITFFT(data):
    n = len(data)
    idx = CalcIdx(n)
    rotation = CAlcRotatingFactor(n)

    # 时间域进行奇偶抽取载入
    result = []
    for  i in idx:
        result.append(data[i])
    result = np.array(result)

    steps = np.int16(np.log2(n))  # 级数
    for i in range(steps):
        div = 1 << (steps - i - 1)
        tmpN = 1 << (i + 1)
        tmpN2 = 1 << i      # tmpN / 2
        tmpN3 = steps - i - 1   # log2(n) - log2(tmpN)
        for j in range(div):    # 每一个部分进行计算
            sI = j * tmpN
            mI = sI + tmpN2
            eI = (j + 1) * tmpN

            # 先进行复数乘法
            for q in range(0, tmpN2):
                result[q + mI] *= rotation[q << tmpN3]

            # 进行复数加法
            tmp1 = result[sI: mI] + result[mI: eI]
            tmp2 = result[sI: mI] - result[mI: eI]
            result[sI: mI] = tmp1
            result[mI: eI] = tmp2
    return result

测试结果如下：

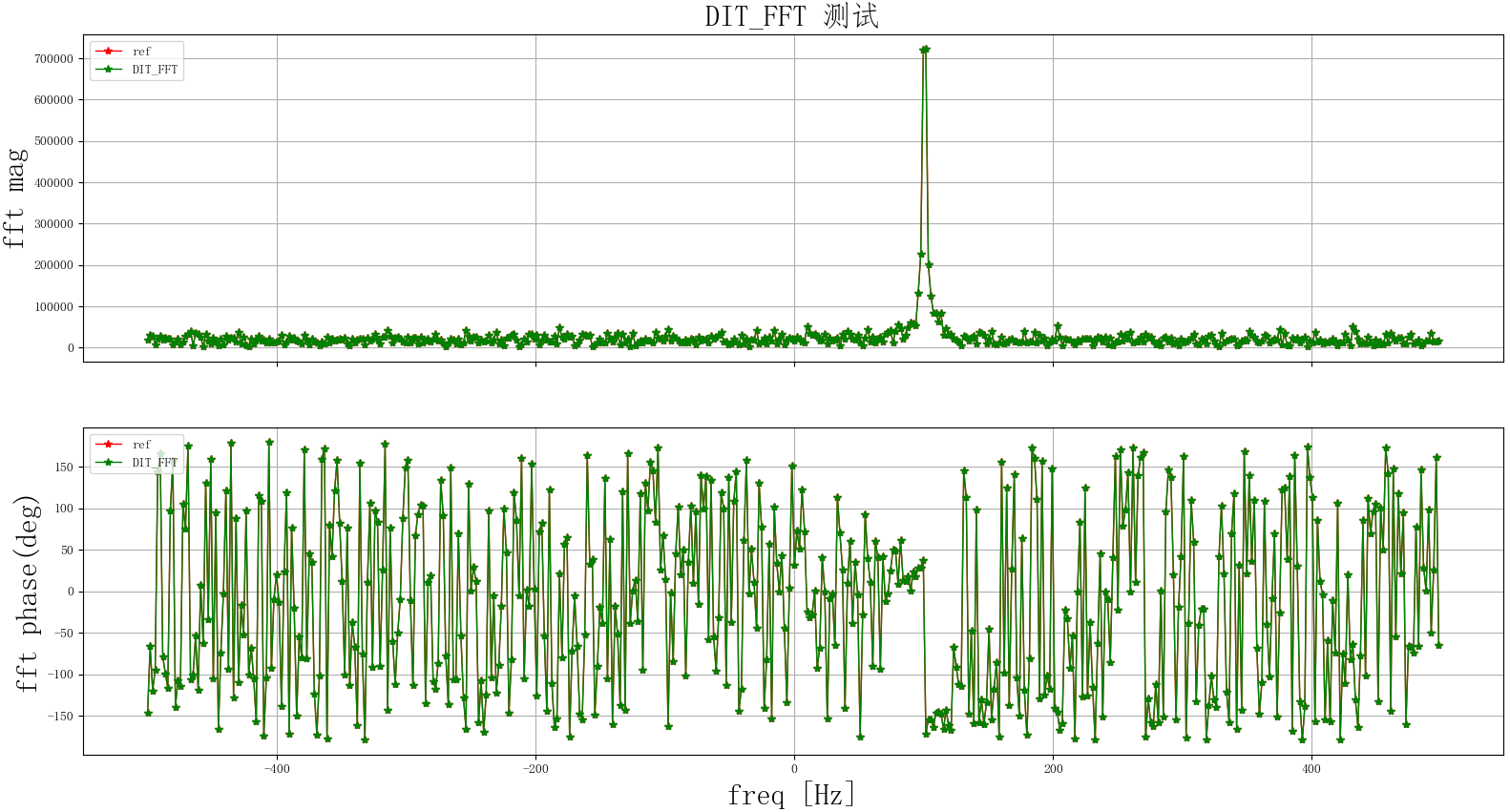
和参考结果完全吻合。

DIF-FFT (Decimation in frequency) Base-2

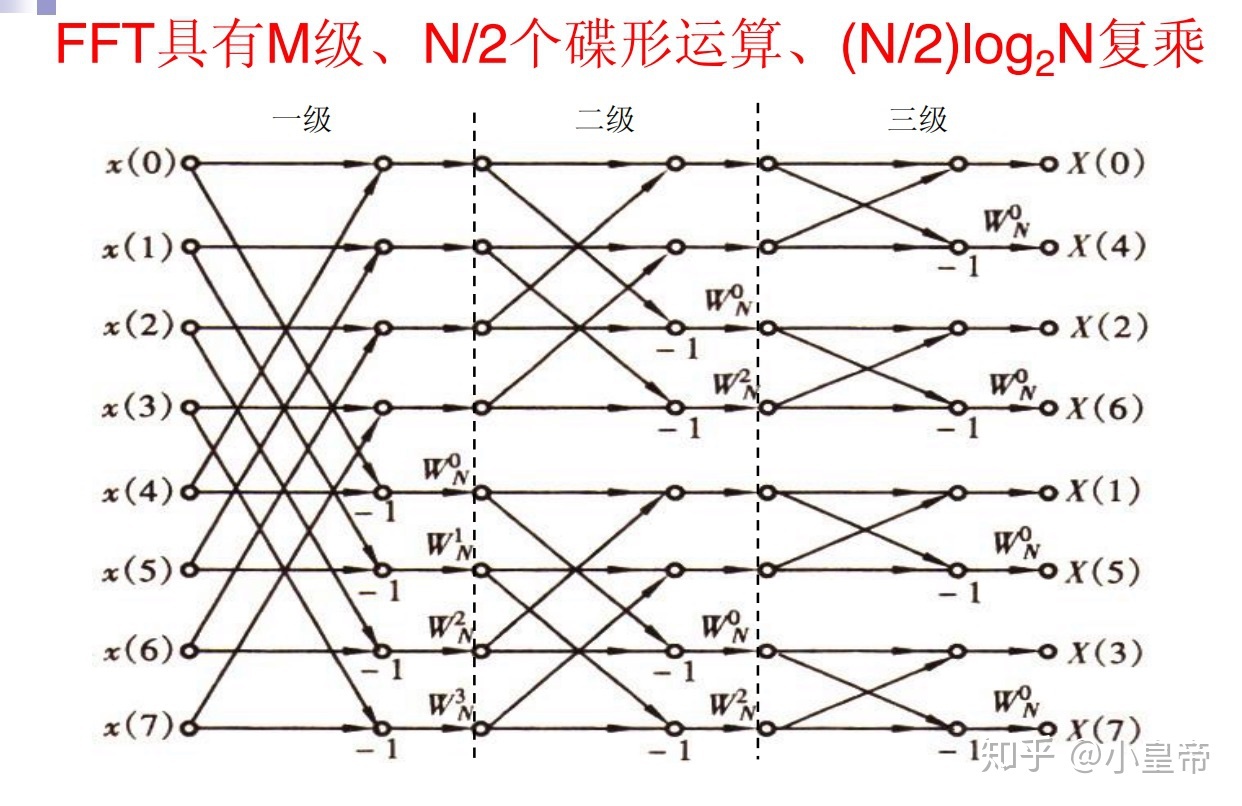
推导过程：

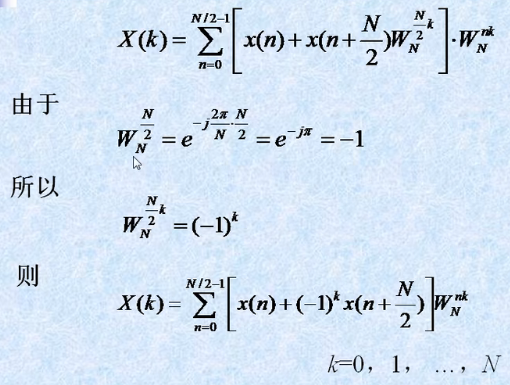
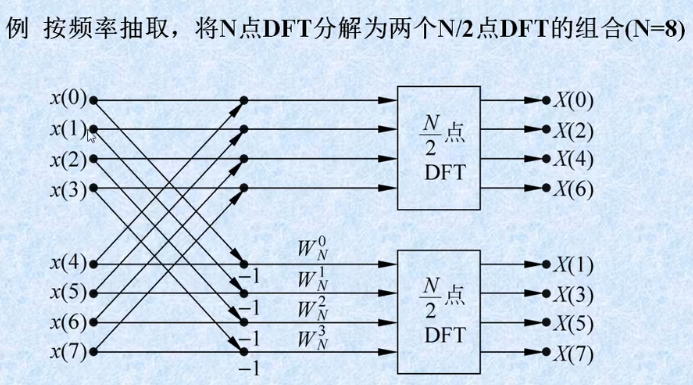
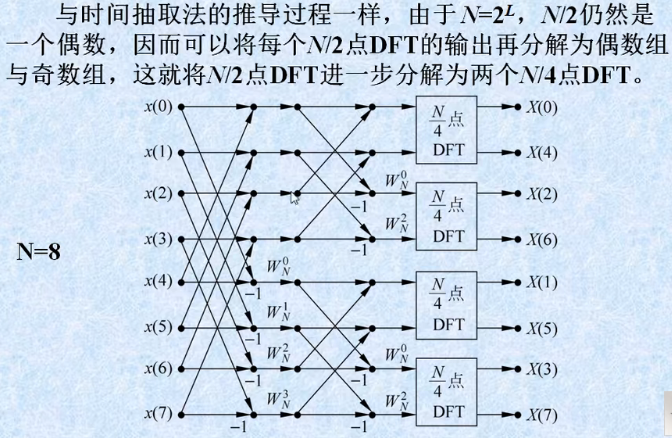
python code 如下：

# DIF-FFT算法
def CalcDIFFFT(data):
    n = len(data)
    rotation = CAlcRotatingFactor(n)

    data = np.array(data)
    steps = np.int16(np.log2(n))  # 级数
    for i in range(steps):
        div = 1 << i
        tmpN = 1 << (steps - i)
        tmpN2 = tmpN >> 1      # tmpN / 2
        tmpN3 = i              # log2(n) - log2(tmpN)
        for j in range(div):    # 每一个部分进行计算
            sI = j * tmpN
            mI = sI + tmpN2
            eI = (j + 1) * tmpN

            # 先进行复数加法
            tmp1 = data[sI: mI] + data[mI: eI]
            tmp2 = data[sI: mI] - data[mI: eI]

            # 再进行复数乘法
            for q in range(0, tmpN2):
                tmp2[q] *= rotation[q << tmpN3]
            # save
            data[sI: mI] = tmp1
            data[mI: eI] = tmp2

    # 频域奇偶抽取进行复原
    idx = CalcIdx(n)
    result = np.zeros((n,), dtype=np.complex128)
    for  i in range(n):
        result[idx[i]] = data[i]

    return result

测试结果如下：

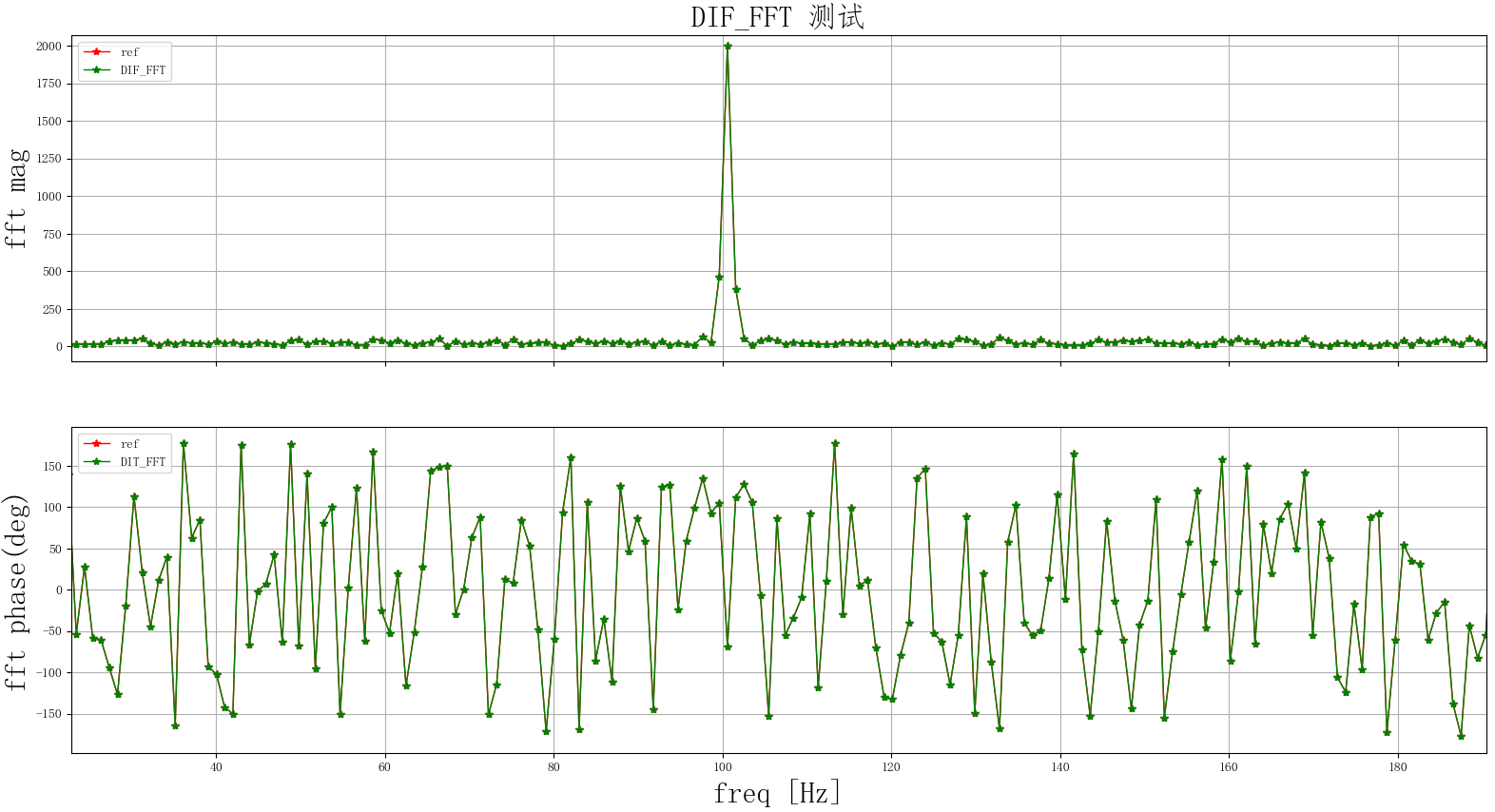
DIF-FFT DIT-FFT 区别

IDFT IFFT

旋转因子指数变极性法

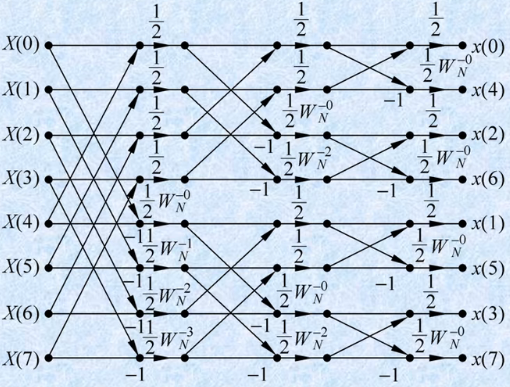
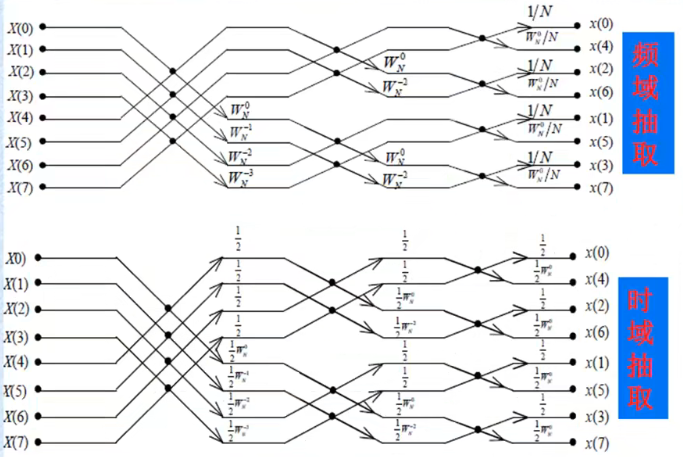
python 代码如下：

# DIT-IFFT算法
# （通过改变DIF-FFT的旋转因子符号，再除以N实现）
def CalcDITIFFT(data):
    n = len(data)
    rotation = CalcInverseRotatingFactor(n)

    data = np.array(data)
    steps = np.int16(np.log2(n))  # 级数
    for i in range(steps):
        div = 1 << i
        tmpN = 1 << (steps - i)
        tmpN2 = tmpN >> 1      # tmpN / 2
        tmpN3 = i              # log2(n) - log2(tmpN)
        for j in range(div):    # 每一个部分进行计算
            sI = j * tmpN
            mI = sI + tmpN2
            eI = (j + 1) * tmpN

            # 先进行复数加法
            tmp1 = data[sI: mI] + data[mI: eI]
            tmp2 = data[sI: mI] - data[mI: eI]

            # 再进行复数乘法
            for q in range(0, tmpN2):
                tmp2[q] *= rotation[q << tmpN3]
            # save
            data[sI: mI] = tmp1 / 2     # 每一级需要除以1/2
            data[mI: eI] = tmp2 / 2

    # 时域奇偶抽取进行复原
    idx = CalcIdx(n)
    result = np.zeros((n,), dtype=np.complex128)
    for  i in range(n):
        result[idx[i]] = data[i]

    return result

# DIF-IFFT算法
# （通过改变DIT-FFT的旋转因子符号，再除以N实现）
def CalcDIFIFFT(data):
    n = len(data)
    idx = CalcIdx(n)
    rotation = CalcInverseRotatingFactor(n)

    # 频域进行奇偶抽取载入
    result = []
    for  i in idx:
        result.append(data[i])
    result = np.array(result)

    steps = np.int16(np.log2(n))  # 级数
    for i in range(steps):
        div = 1 << (steps - i - 1)
        tmpN = 1 << (i + 1)
        tmpN2 = 1 << i      # tmpN / 2
        tmpN3 = steps - i - 1   # log2(n) - log2(tmpN)
        for j in range(div):    # 每一个部分进行计算
            sI = j * tmpN
            mI = sI + tmpN2
            eI = (j + 1) * tmpN

            # 先进行复数乘法
            for q in range(0, tmpN2):
                result[q + mI] *= rotation[q << tmpN3]

            # 再进行复数加法
            tmp1 = result[sI: mI] + result[mI: eI]
            tmp2 = result[sI: mI] - result[mI: eI]
            result[sI: mI] = tmp1 / 2   # 每一级需要除以1/2
            result[mI: eI] = tmp2 / 2
    return result

测试结果：

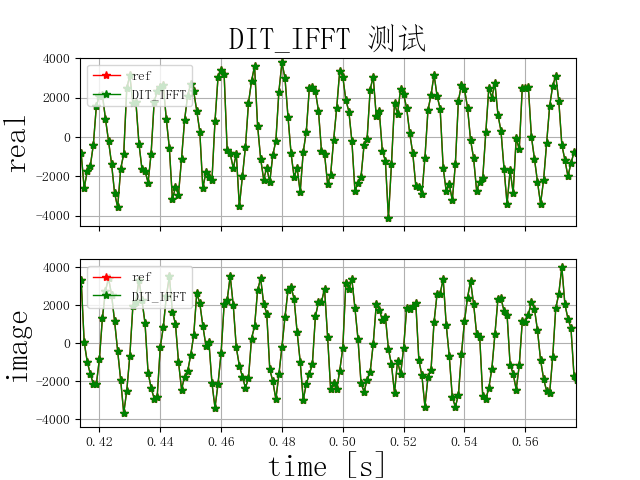
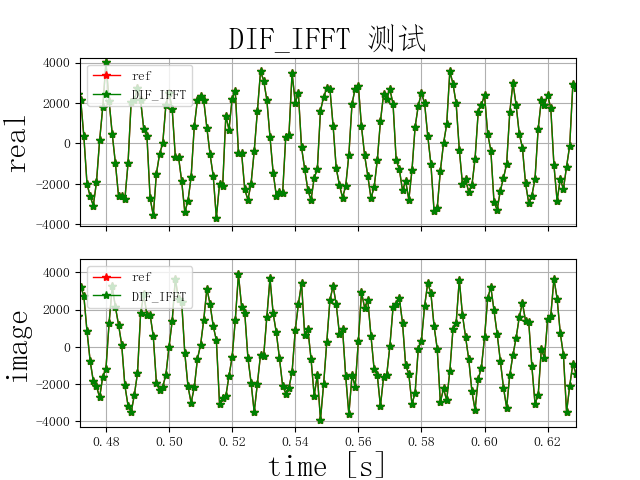
直接调用FFT子程序法

方法一：

方法二：

python code 如下：

# IFFT算法（直接调用FFT模块进行计算）
# 方法一：先去共轭，FFT， 在取共轭，除以N
def CalcIFFT1(data):
    data = np.conjugate(data)
    tmp = CalcDITFFT(data)
    return np.conjugate(tmp) / len(data)

# IFFT算法（直接调用FFT模块进行计算）
# 方法二：FFT， 时间域内进行平移，除以N
def CalcIFFT2(data):
    tmp = CalcDITFFT(data)
    N = len(data)
    tmp1 = []
    for n in range(N):
        if n == 0:
            tmp1.append(tmp[0])
            continue
        tmp1.append(tmp[N - n])
    return np.array(tmp1) / N

测试结果和原始输入数据一致。