代码随想录算法训练营|数组内容复习
数组内容复习
二分查找
704. 二分查找 主要是要注意两点:一是在进行middle位置判断的时候,要看的是nums[middle]位于哪侧区间哪个边界,二就是看上一步哪侧区间哪个边界的时候,要看的是有target在的那一侧区间。
比如:[left, 0, 0, middle, targets, 0, right],此时的targets位于右区间,nums[middle]就是右区间的左边界,所以直接更新left即可
左闭右闭
点击查看代码
class Solution {
public:
int search(vector<int>& nums, int target) {
// 左闭右闭
int left = 0;
int right = nums.size() - 1;
int i = 0;
while (left <= right) {
cout << i++ << endl;
int middle = (left + right) / 2;
if (nums[middle] < target) {
left = middle + 1;
// cout << left << endl;
}
else if (nums[middle] > target) {
right = middle - 1;
// cout << "right" << endl;
}
else return middle;
}
return -1;
}
};
左闭右开
点击查看代码
class Solution {
public:
int search(vector<int>& nums, int target) {
// 左闭右开
int left = 0;
int right = nums.size();
while (left < right) {
int middle = (left + right) / 2;
if (nums[middle] < target) left = middle + 1;
else if (nums[middle] > target) right = middle;
else return middle;
}
return -1;
}
};
移除元素
27. 移除元素 这个题用双指针很简单,就是力扣上按理来说只需要一个k记录并返回即可。但是他的判题要看的却是数组能不能对的上
点击查看代码
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int slow = 0, fast = 0;
int k = 0;
for (;fast < nums.size(); fast++) {
if (nums[fast] != val) {
k++;
// nums[slow++] = nums[fast];
}
}
cout << k << endl;
return k;
}
};
有序数组的平方
977. 有序数组的平方 这里再用双指针写的时候,需要注意的是在for循环内部的条件判断,刚开始我写的是if-else if 两种情况,没有另外写if (nums[left] == nums[right]),那其实如果两个指针合拢了的话,那么循环就没有出口了,会一直停在指向的同一个数,所以会超时了
点击查看代码
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
for (int i = 0; i < nums.size(); i++) {
nums[i] = nums[i] * nums[i];
}
vector<int> result(nums.size(), 0);
int k = nums.size() - 1;
int left = 0, right = nums.size() - 1;
for (; left <= right;) {
if (nums[left] < nums[right]) {
result[k] = nums[right];
k--;
right--;
}
else {
result[k] = nums[left];
k--;
left++;
}
}
return result;
}
};
长度最小的子数组
这个题比较核心的地方就是在于是一个for-while循环,并在while循环下面内嵌了对i的控制。感觉好多了,有了上次的经验,这次就没有怎么卡壳
点击查看代码
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int sum = 0, subl = INT_MAX;
int i = 0, result = 0;
for (int j = 0; j < nums.size(); j++) {
sum += nums[j];
while (sum >= target) {
sum -= nums[i];
result = j - i + 1;
if (result < subl) subl = result;
i++;
}
}
return subl == INT_MAX ? 0 : subl;
}
};
螺旋矩阵Ⅱ
59. 螺旋矩阵 II 这个题还是细节很多了,忘记了要加上offset的判断,还有对startx和starty的处理也很重要。真是一入循环深似海
点击查看代码
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int loop = n / 2;
cout << loop << endl;
int startx = 0;
int starty = 0;
int count = 1;
int offset = 1;
vector<vector<int>> matrix(n, vector<int>(n, 0));
while (loop--) {
int i;
int j;
for (j = starty; j < n - offset; j++) {
matrix[startx][j] = count++;
}
for (i = startx; i < n - offset; i++) {
matrix[i][j] = count++;
}
for (; j > starty; j--) {
matrix[i][j] = count++;
}
for (; i > startx; i--) {
matrix[i][j] = count++;
}
startx++;
starty++;
offset++;
}
if (n % 2 != 0) matrix[n / 2][n / 2] = count;
return matrix;
}
};
区间和
58. 区间和 这个题用正常暴力看着其实再正常不过了,不过真的是会时间超限,k哥在这道题上额外制作了大数据量查询,就是为了引入前缀和。很好用的方法。
思路很简单,就是直接计算前面的所有的前缀和,在输出区间的时候,就不用循环了,而是\(O(1)\)直接进行相减
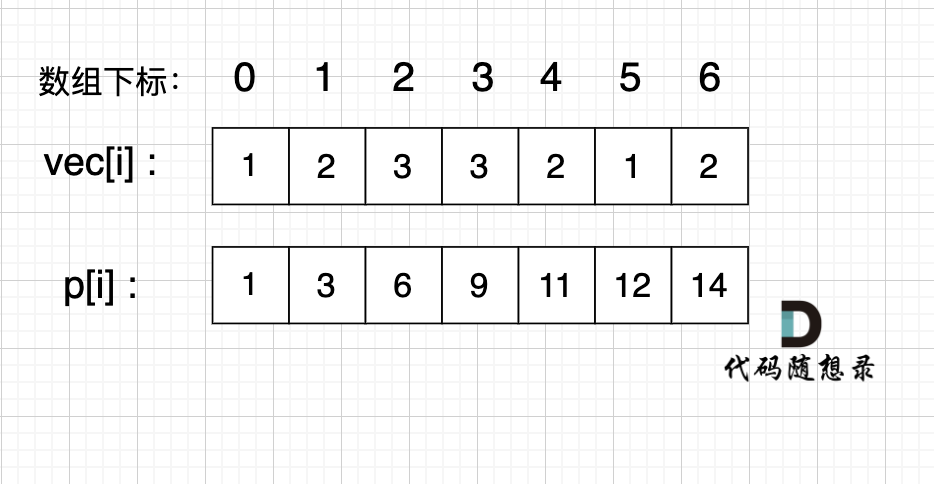
点击查看代码
#include<iostream>
#include<vector>
using namespace std;
int main() {
int n, x, a, b;
cin >> n;
vector<int> p(n, 0);
int sum = 0;
for (int i = 0; i < n; i++) {
cin >> x;
sum += x;
p[i] = sum;
}
while (cin >> a >> b) {
int result = 0;
cout << p[b] - p[a - 1] << endl;
}
}
开放商购买土地
44. 开发商购买土地 今天的这道题太不容易了,全都是细节。
梳理
- 仍然是前缀和的思路,分成两部分进行,首先是按列进行划分

- 之后按行进行划分

-
之后就是,比如按列划分,那么对左右两部分的土地权值单独进行累加,然后添加到一个
result数组里,之后将该分割线机型移动,重复上面的步骤,按行进行划分也是一样。 -
最后遍历一遍result数组,得到最小的值即可
注意
-
首先就是需要对输入的数据进行存储,这次一开始竟然没有存😅,输出都是0
-
另外就是对记录前缀和的数组p进行遍历的时候,注意,如果是按列划分,那么一定要先j是外循环,i是内层循环,因为要累加左右两侧的值。同样,如果是按行划分,那么就是i是外层循环,j是内存循环,因为要累加上下两侧的值。
-
下面还有一些需要注意的地方
举个例子,在按列划分的时候,注意i的遍历也是从0开始的,对于左侧的所有的和,就是p[i][j],而对于右侧的所有的和,应该用p[i][m - 1] - p[i][j],为什么不是p[i][m - 1] - p[i][j - 1]呢?就像之前的区间和一样,是因为右侧的和不算上value[i][j],所以应该从p[i][m - 1]中把他也减掉。这个具体可以画个图出来,更直观一些。
还有就是每次更新完记得对sumLeft和sumRight赋值0
for (int j = 0; j < m - 1; j++) {
for (int i = 0; i < n; i++) {
left = p[i][j];
right = p[i][m - 1] - p[i][j];
// cout << left << " " << right << endl;
sumLeft += left;
sumRight += right;
}
result.push_back(abs(sumLeft - sumRight));
sumLeft = 0;
sumRight = 0;
}
- 在写的过程中,明显发现对一些库函数的使用还不熟悉,有时候就和python混了,比如c++能不能用min直接求一个vector的值呀?怎么用memset对二维数组赋值全0呀?之类的,还是不熟。
贴代码
点击查看代码
#include<iostream>
#include<vector>
#include<algorithm>
#include<limits.h>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<int>> value(n, vector<int>(m, 0));
int num;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
cin >> num;
value[i][j] = num;
}
}
vector<vector<int>> p(n, vector<int>(m, 0));
vector<int> result;
int sum = 0;
// 先处理按列进行划分的情况
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
sum += value[i][j];
p[i][j] = sum;
}
sum = 0;
}
int left = 0, right = 0;
int sumLeft = 0, sumRight = 0;
for (int j = 0; j < m - 1; j++) {
for (int i = 0; i < n; i++) {
left = p[i][j];
right = p[i][m - 1] - p[i][j];
// cout << left << " " << right << endl;
sumLeft += left;
sumRight += right;
}
result.push_back(abs(sumLeft - sumRight));
sumLeft = 0;
sumRight = 0;
}
// 再按照行进行划分
sum = 0;
vector<vector<int>> p1(n, vector<int>(m, 0));
for (int j = 0; j < m; j++) {
for (int i = 0; i < n; i++) {
sum += value[i][j];
p1[i][j] = sum;
}
sum = 0;
}
// for (int i = 0; i < n; i++) {
// for (int j = 0; j < m; j++) {
// cout << p1[i][j] << " ";
// }
// cout << endl;
// }
int up = 0, down = 0;
int sumUp = 0, sumDown = 0;
for (int i = 0; i < n - 1; i++) {
for (int j = 0; j < m; j++) {
up = p1[i][j];
down = p1[n - 1][j] - p1[i][j];
// cout << up << " " << down << endl;
sumUp += up;
sumDown += down;
}
result.push_back(abs(sumUp - sumDown));
sumUp = 0;
sumDown = 0;
}
int dis = INT_MAX;
for (int i = 0; i < result.size(); i++) {
dis = min(dis, result[i]);
// cout << result[i] << endl;
}
cout << dis << endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号