代码随想录算法训练营第53天|Floyd 算法、A * 算法、最短路问题总结
Floyd 算法
2025-03-29 15:59:11 星期六
题目描述:97. 小明逛公园
文档讲解:代码随想录(programmercarl)Floyd 算法精讲
要点
-
Floyd求解的是多源最短路问题,求多个起点到多个终点的多条最短路径。和dijkstra和Bellman_ford的区别就是后两者每次只能输出一条最短路径(其起点和终点是每次需要设置好的),如果还需要输出一条,那就再运行一遍。
-
Floyd对边的正负权值没有要求,其核心思想是动态规划
动归五部曲
-
确定dp数组的含义,Floyd的dp数组也是存储图的数组,有些特别的是,这里的dp数组是三维的。
grid[i][j][k] = m表示结点i到结点j以[i...k]集合中的一个结点为中间结点的最短距离为grid[i][j][k] -
确定递归公式。首先这里,如果求节点1 到 节点9 的最短距离,那么可以拆分成节点1 到节点5的最短距离 + 节点5到节点9的最短距离,也可以拆分成节点1 到节点7的最短距离 + 节点7 到节点9的最短距离。那么取最小的话就是min
同理,如果要经过i到j中以[i...k]集合中的一个中间结点,也就是grid[i][j][k],其前一个状态可以是dp[i][j][k - 1]就是不经过中间的k结点。既然要从前面的状态推导,不经过k,所以对grid[i][j]也需要拆分情况,一种是dp[i][k][k - 1] + dp[k][j][k - 1],另一种就是dp[i][j][k - 1],二者取min。
grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]) -
初始化dp数组
只能 把k 赋值为 0,本题 节点0 是无意义的,节点是从1 到 n。这样初始化是为了方便进行下面的推导,这样的操作在动归中不鲜见
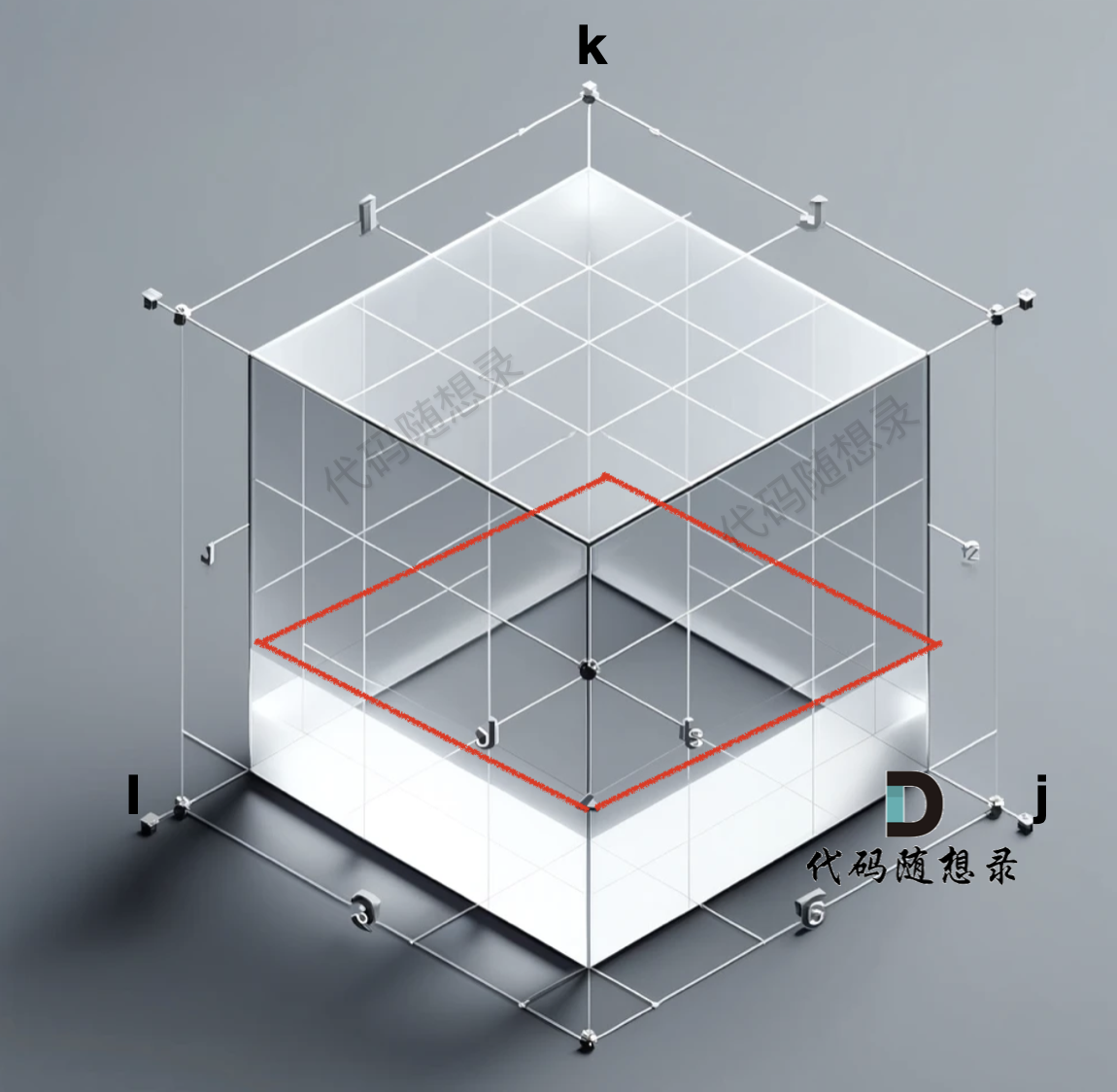
grid数组是一个三维数组,初始化的数据在 i 与 j 构成的平层
-
确定遍历顺序
那么遍历顺序就是一层一层往上遍历即可,从下往上进行推导。所以,整个for循环的结构是
for (int k = 1; k < ...) {
for (int i = 1...) {
for (int j = 1...) {
}
}
}
- 打印dp数组
注意:最后在进行结果输出的时候,输出的是grid[start][end][N],这里k为什么成了N了呢,这里的意思是 节点start 到 节点end 以[1...N] 集合中的一个节点为中间节点的最短距离为grid[start][end][N],这里的N表示一个集合,从里面取谁需要递推公式自己去推导,这里写N只是为了确定范围,不让他少元素。
卡玛网测试
这个题是稿抽象了,前面的动归有点不记得了😂
点击查看代码
#include<iostream>
#include<vector>
using namespace std;
int main() {
int N, M;
cin >> N >> M;
int u, v, w;
vector<vector<vector<int>>> grid(N + 1, vector<vector<int>>(N + 1, vector<int>(N + 1, 10001)));
// 图的存储(初始化dp数组)
for (int i = 0; i < M; i++) {
cin >> u >> v >> w;
grid[u][v][0] = w;
grid[v][u][0] = w;
}
// 观景计划
int Q;
cin >> Q;
//起点和终点
int start, end;
vector<vector<int>> road;
for (int i = 1; i <= Q; i++) {
cin >> start >> end;
road.push_back({start, end});
}
for (int k = 1; k <= N; k++) {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
grid[i][j][k] = min(grid[i][j][k - 1], grid[i][k][k - 1] + grid[k][j][k - 1]);
}
}
}
// for (vector<int> g : road) {
// cout << g[0] << g[1] << endl;
// }
for (int i = 0; i < Q; i++) {
if (grid[road[i][0]][road[i][1]][N] == 10001) cout << -1 << endl;
else cout << grid[road[i][0]][road[i][1]][N] << endl;
}
}
A * 算法
题目描述:127. 骑士的攻击
文档讲解:代码随想录(programmercarl)A * 算法精讲 (A star算法)
要点
- 首先注意图中骑士的走法,
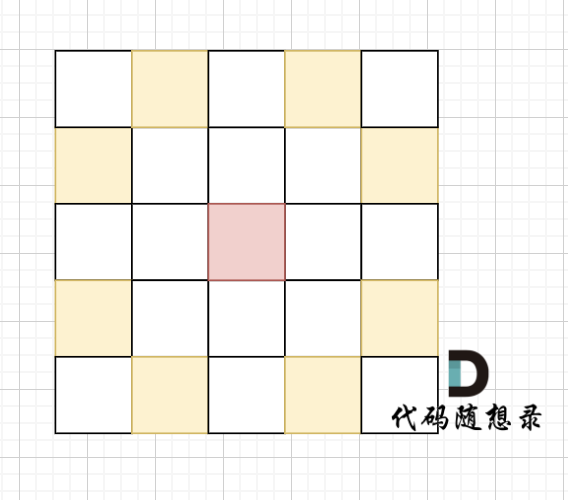
- 在进行dir定义的时候,注意下面的这句话,所以在边界判断时不能
nextx < 0,而是应该nextx < 1
棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界
梳理
- 首先也是用广搜给他搜一遍
k哥做的这个可视化动图也太牛逼了把😲😲,链接贴出来
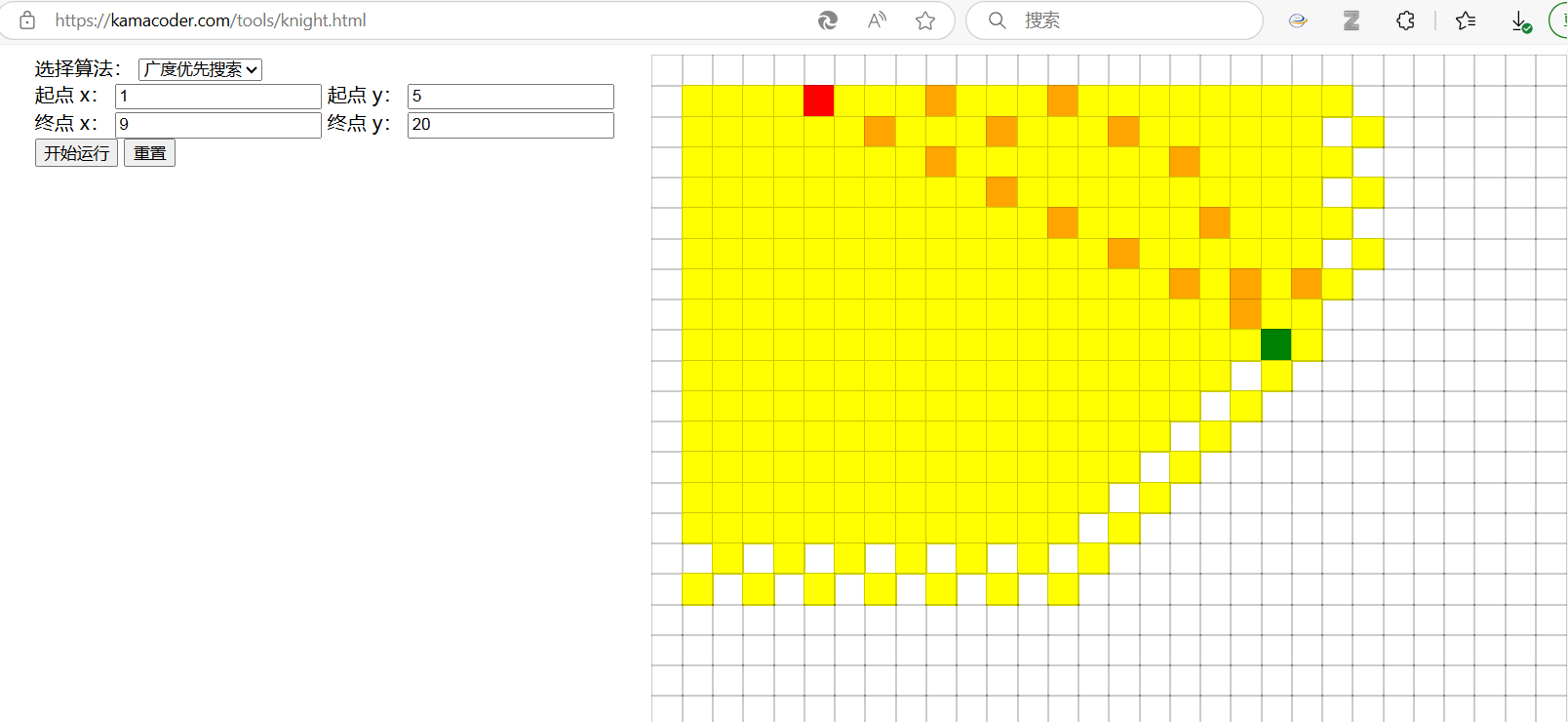
-
引出A*
其实可以从上图看出,广搜会搜到大量的没有用的结点黄色的,而相比较之下。A*的搜索就比较有导向性了。

这里关键就是A的启发式函数。这个启发式函数是怎么考虑的呢?A的启发式函数是用来给广搜(无权图这里用广搜)队列里面的元素进行加权,从而让其有一个按照权从小到大进行排序的优先级队列,对,没错,又是优先级队列。
这里的权是什么呢?为了让这里的权能正确引导骑士从骑士点走向目标点,这里的权用两点间的距离进行表示。每个结点的权值为F,给出公式\(F=G+H\),这两个距离在纸上一画就很明了了
-
[1] G:起点达到目前遍历节点的距离(也叫路径成本)
-
[2] H:目前遍历的节点到达终点的距离(也叫启发式估计)
-
[3] F:也叫综合评分
那如何计算距离呢?
-
[1] 曼哈顿距离。\(d=|x_1-x_2|+|y_1-y_2|\)
-
[2] 欧氏距离。\(d=\sqrt{{x_1-x_2}^2}+\sqrt{{y_1-y_2}^2}\)
-
[3] 切比雪夫距离。\(d=max(|x_1-x_2|+|y_1-y_2|)\)
从而通过这里的权直接引导骑士走向终点,同时需要知道就是三个距离中能直接体现出点到点的真正距离的是欧式距离,所以下面的计算也采用欧式距离。
之后,每次从队列中弹出的,就不再仅仅是广搜之前按顺序添加的元素了,而是在原先顺序之上加权排列过的元素。那么就可以说这样弹出元素的顺序就是有导向性了
-
关于A*的一些要点
-
A * 只擅长给出明确的目标 然后找到最短路径。
-
A * 算法 并不是一个明确的最短路算法,A * 算法搜的路径如何,完全取决于 启发式函数怎么写。
-
A * 算法并不能保证一定是最短路,因为在设计 启发式函数的时候,要考虑 时间效率与准确度之间的一个权衡。
-
A* 解决不了这种:给出多个可能的目标,然后在这多个目标中选择最近的目标,他只擅长给出明确目标,然后找到最短路
-
大致代码内容
- 首先,这里定义了一个新的结构体Knight,其有5个变量,x和y表示当前的坐标,然后就是上面的G,H和F
struct Knight{
int x,y;
int g,h,f;
bool operator < (const Knight & k) const{ // 重载运算符, 从小到大排序
return k.f < f;
}
};
关于重载运算符
returnType operator < (const Type& other) const;
- operator <:表示- 重载小于运算符(<)。
- const Type& other:表示另一个与当前对象比较的对象(即作为参数传入的对象)。
- const:表示该函数不会修改当前对象的成员变量。
这里为什么需要重载这个小于号,问了一下GPT
如果你有一个 类类型,并希望能够使用 < 来比较两个对象的大小,通常情况下是不可以直接比较的,因为编译器不知道如何比较两个类对象。这时你需要重载 < 运算符。
- 欧拉距离计算的函数,这里不开根号
int Heuristic(const Knight& k) { // 欧拉距离
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2); // 统一不开根号,这样可以提高精度
}
卡玛网测试
广搜代码
这个会超时
点击查看代码
#include<iostream>
#include<vector>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2] = {-2, 1, -1, 2, 1, 2, 2, 1, 2, -1, 1, -2, -1, -2, -2, -1};
void bfs(int a1, int a2, int b1, int b2) {
queue<pair<int, int>> que;
que.push({a1, a2});
while (!que.empty()) {
pair<int, int> cur = que.front();
que.pop();
if (cur.first == b1 && cur.second == b2) break;
for (int i = 0; i < 8; i++) {
int nextx = cur.first + dir[i][0];
int nexty = cur.second + dir[i][1];
if (nextx < 1 || nextx >= 1000 || nexty < 1 || nexty >= 1000) continue;
if (!moves[nextx][nexty]) {
moves[nextx][nexty] = moves[cur.first][cur.second] + 1;
que.push({nextx, nexty});
}
}
}
}
int main() {
int n;
cin >> n;
int a1, a2, b1, b2;
vector<vector<int>> grid;
// 图的存储
for (int i = 0; i < n; i++) {
memset(moves,0,sizeof(moves));
cin >> a1 >> a2 >> b1 >> b2;
bfs(a1, a2, b1, b2);
cout << moves[b1][b2] << endl;
}
}
A*算法
这里有两个需要注意的地方
-
第一个这是一个很隐蔽的错误
在A*的开头,就会定义一个
int b1, b2;,这个是用来计算下面的距离终点的欧式距离,来算h启发式估计的。但是我在一开始不注意,在int main主函数中又定义了一个int a1, a2, b1, b2;,这样就会导致出现前面的全局变量失效,如果直接打印Heuristic里面的b1,b2是会报越界的。所以解决方法就是在主函数中把b1和b2的定义取消了,那么结果就正常了,同时打印也可以输出了 -
在A*函数中,刚开始我是这么写的
for (int i = 0; i < 8; i++) {
int nextx = cur.x + dir[i][0];
int nexty = cur.y + dir[i][1];
if (nextx < 1 || nextx > 1000 || nexty < 1 || nexty > 1000) continue;
if (!moves[nextx][nexty]) {
moves[nextx][nexty] = moves[cur.x][cur.y] + 1;
next.x = nextx;
next.y = nexty;
next.g = cur.g + 5;
next.h = Heuristic(cur);
next.f = next.g + next.h;
que.push(next);
}
}
这个错误刚开始也是一直没有找到,打印出来的结果一直都是

最后才发现是计算欧氏距离的时候传错了,next.h = Heuristic(cur);,应该是next.h = Heuristic(next);才对
-
关于
if(!moves[next.x][next.y]),这里的意思就是让算法在走的时候不重复走过格子,因为没有走过的格子都是0,那么!moves[next.x][next.y]就代表1,就可以让条件判断通过,从而继续往下走。但是如果是一个有数值的格子,那么!moves[next.x][next.y]就是0了,所以就不走了。这个必须加上,因为题目求得是最短路径,一旦重复走了,就不是最短的了 -
还有一点就是为什么主函数里需要进行队列清空,
while(!que.empty()) que.pop();,这个其实也好理解,就是在队列中,每次for循环需要添加8个方向的走向进入到队列,但是每次只pop掉按权值由小到大排列的第一个,所以剩下的还在队列中,此时如果一旦发现等于终点,那么就直接推出了。如果不清空,输入下一轮起点和终点的时候就必然有问题了。
最后附上代码
点击查看代码
#include<iostream>
#include<vector>
#include<queue>
#include<string.h>
using namespace std;
int moves[1001][1001];
int dir[8][2] = {-2, 1, -1, 2, 1, 2, 2, 1, 2, -1, 1, -2, -1, -2, -2, -1};
int b1, b2;
struct Knight{
int x, y;
int g, h, f;
bool operator < (const Knight &k) const{
return k.f < f;
}
};
int Heuristic(const Knight &k) {
// cout << b1 << endl;
return (k.x - b1) * (k.x - b1) + (k.y - b2) * (k.y - b2);
}
priority_queue<Knight> que;
void astar(const Knight &k) {
Knight cur, next;
que.push(k);
while(!que.empty()) {
cur = que.top();
que.pop();
if (cur.x == b1 && cur.y == b2) break;
for (int i = 0; i < 8; i++) {
int nextx = cur.x + dir[i][0];
int nexty = cur.y + dir[i][1];
if (nextx < 1 || nextx > 1000 || nexty < 1 || nexty > 1000) continue;
if (!moves[nextx][nexty]) {
moves[nextx][nexty] = moves[cur.x][cur.y] + 1;
next.x = nextx;
next.y = nexty;
// 计算F
next.g = cur.g + 5;
next.h = Heuristic(next);
next.f = next.g + next.h;
que.push(next);
}
}
}
}
int main() {
int n;
cin >> n;
int a1, a2;
vector<vector<int>> grid;
// 图的存储
for (int i = 0; i < n; i++) {
memset(moves,0,sizeof(moves));
cin >> a1 >> a2 >> b1 >> b2;
Knight start;
start.x = a1;
start.y = a2;
start.g = 0;
start.h = Heuristic(start);
start.f = start.g + start.h;
astar(start);
while(!que.empty()) que.pop(); // 队列清空
cout << moves[b1][b2] << endl;
}
}
最短路问题总结
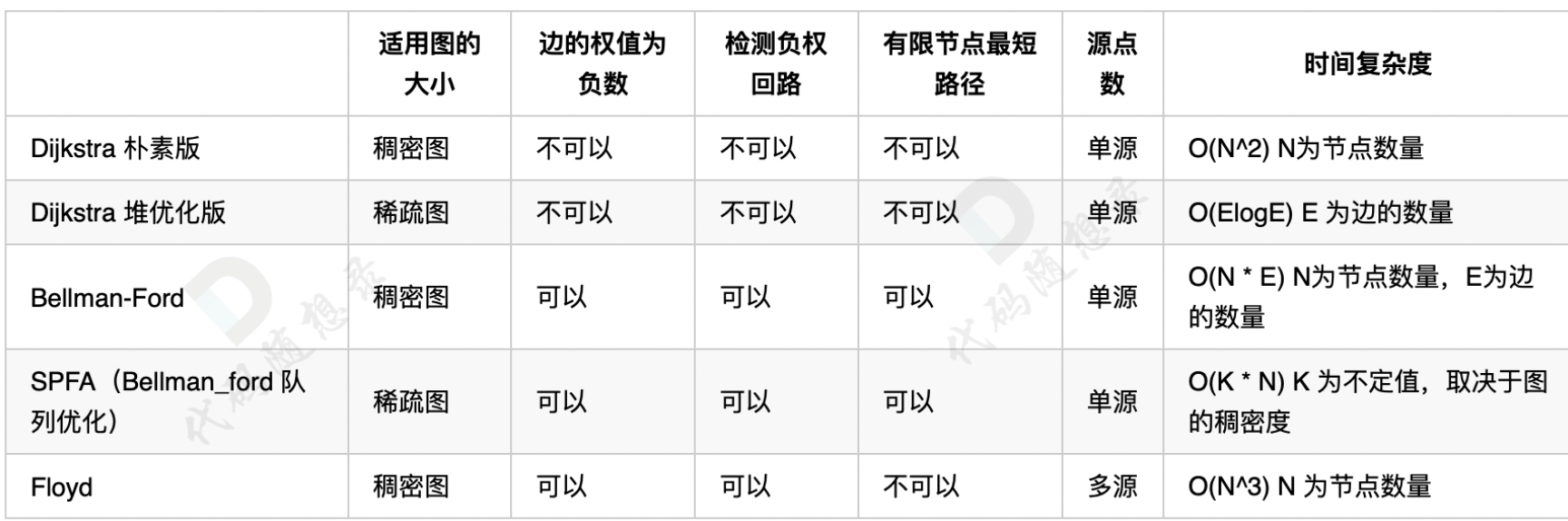
本次的最短路问题主要介绍了
- dijkstra朴素版
- dijkstra堆优化版
- Bellman_ford
- Bellman_ford队列优化版
- Bellman_ford判断负权回路
- Bellman_ford之单源有限最短路
- Floyd
- Astar
其中的Astar算是启发式算法,不是严格的最短路算法
-
dijkstra
适用于稠密图,没有负权边的情况。dijkstra三部曲,是和prim很像的,用邻接矩阵存储,同样用的也是minDist数组
-
dijkstra堆优化版
适用于稀疏图,同样不能有负权边。dijkstra朴素版针对于点,堆优化版则是针对于于边,改用邻接表,进行稀疏的存储。核心改动就是三部曲中第一步,引入优先级队列构造小顶堆,得到每一个离源点最近的结点,来更新minDist数组
-
Bellman_ford
这个适用来解决负权边的,同时还能检测负权回路,以及有限个结点的最短路,还是比较全能的。其算法的核心就俩字————“松弛”,松弛一遍得到 从起点出发 与起点一条边相连结点的 最短距离
-
Bellman_ford队列优化版
这个就是为了减少Bellman_ford算法里出现的多余“松弛”,每次只需要让当前结点和指向结点之家的边进行松弛即可。所以,遍历这些指向的结点进行松弛计算
minDist[side.to] > minDist[cur] + side.val,之后再将这些结点加入到队列中

 答案在路上,自由在风里
答案在路上,自由在风里


 浙公网安备 33010602011771号
浙公网安备 33010602011771号