代码随想录算法训练营第52天|Bellman_ford 队列优化算法（又名SPFA）、bellman_ford之判断负权回路、bellman_ford之单源有限最短路

Bellman_ford 队列优化算法（又名SPFA）

2025-03-27 18:59:23 星期四

题目描述：94. 城市间货物运输 I
文档讲解：代码随想录(programmercarl)Bellman_ford 队列优化算法（又名SPFA）

Bellman_ford队列优化算法，核心就是减少在Bellman_ford算法中出现的一些多余计算。这些多余计算是从哪里来的呢？

在Bellman_ford中，每次进行松弛，都需要对所有边进行一遍松弛，但是有些边的to指向的结点的minDist是INT_MAX，也就是还没有被计算过，那么对这些边进行松弛，就是无效的计算。

所以队列优化版本的思路就是，把所有计算过的结点添加到一个队列中，然后在进行松弛的时候，直接从队列中取元素，对该元素指向的所有结点进行松弛，对他没有指向的结点(还是INT_MAX)则不进行松弛。这里的做法有点像拓扑排序，都是通过一个中间队列，来进行过渡

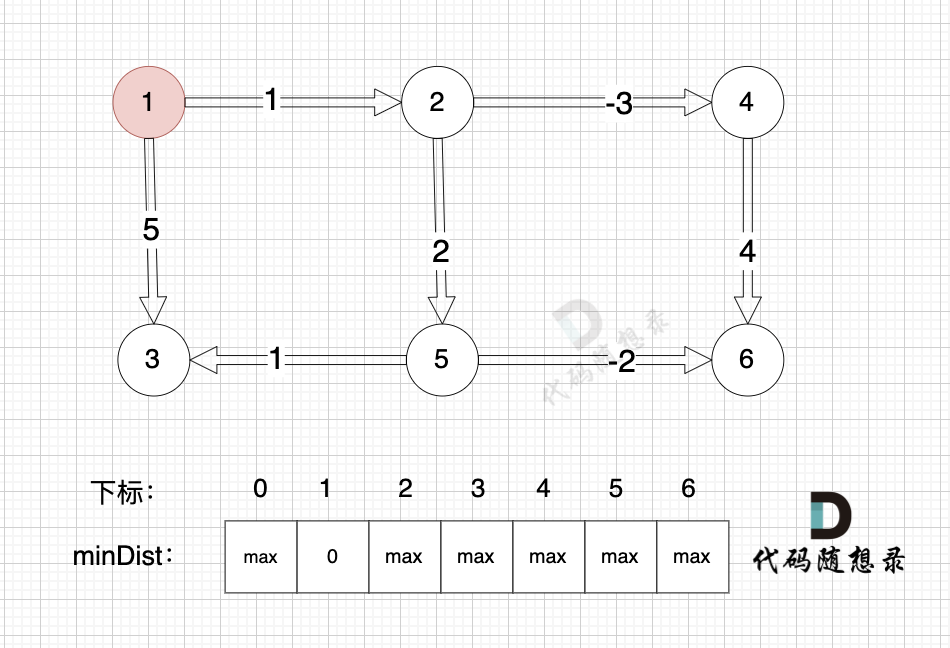
梳理

图的存储，因为要知道一个结点指向的所有结点，那么就需要用到邻接表，当然了临界表存储的时候除了当前结点指向的下一个结点，还需要有变的权值，所以就用到了上次dijkstra堆优化那里定义的结构体Edge
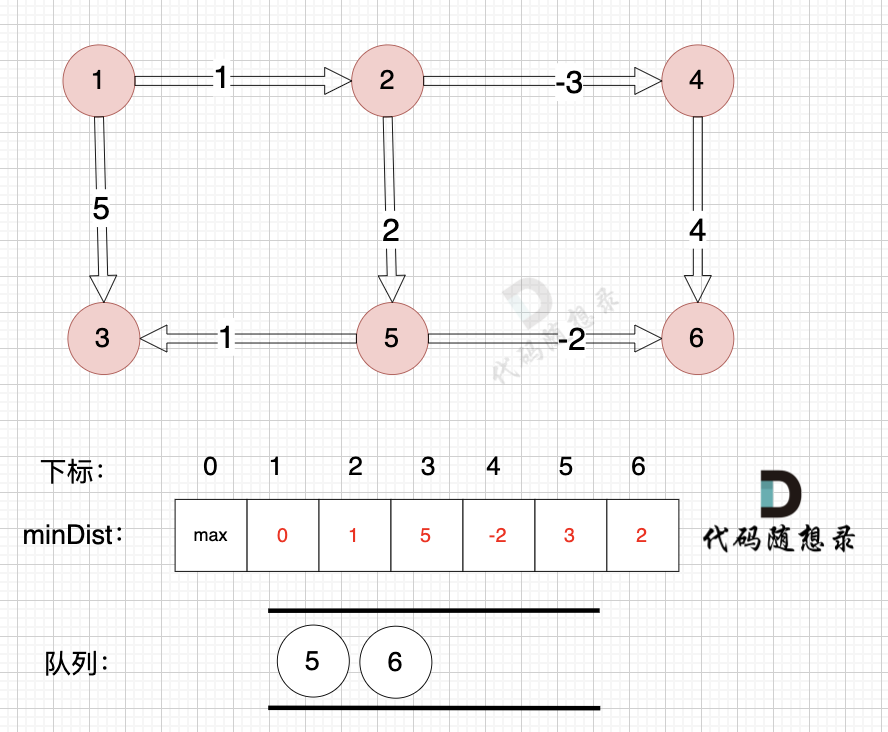
首先将1加入队列，之后进入while (!que.empty())循环，取出队列首元素，将当前结点指向的所有结点进行松弛操作，松弛完了将这些结点再加入队列中进行下一轮的松弛。

同时为了避免往队列中添加相同的元素。如下图队列中已有的元素是5和6，现在是将5取出，需要将3和6进行添加，而队列中已经有6了，所以不用再重复添加。这里引入一个visited数组，在每次在进行队列元素添加的时候，visited[cur]必须是false才能进行添加，一旦入队，就标记为true访问过，一旦出队，就标记为false。

卡玛网测试

点击查看代码

#include<vector>
#include<iostream>
#include<queue>
#include<climits>
#include<list>
using namespace std;

struct Edge{
    int to;
    int val;

    Edge(int t, int w): to(t), val(w) {}
};

int main() {
    int n, m;
    cin >> n >> m;
    int s, t, v;
    vector<list<Edge>> grid(n + 1);

    // 图的存储
    for (int i = 0; i < m; i++) {
        cin >> s >> t >> v;
        grid[s].push_back(Edge(t, v));
    }

    vector<int> minDist(n + 1, INT_MAX);
    minDist[1] = 0;
    queue<int> que;
    que.push(1);
    vector<bool> visited(n + 1, false);
    visited[1] = true;

    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        visited[cur] = false;
        for (Edge side : grid[cur]) {
            if (visited[cur] != true && minDist[side.to] > minDist[cur] + side.val) {
                minDist[side.to] = minDist[cur] + side.val;
                que.push(side.to);
                visited[cur] = false;
            }
        }
    }

    if (minDist[n] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[n] << endl;
}

bellman_ford之判断负权回路

题目描述：卡玛网95. 城市间货物运输 II
文档讲解：代码随想录(programmercarl)bellman_ford之判断负权回路

本题的不同就是增加了负权回路的判断

负权回路是指一系列道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益

Bellman_ford版

这道题在Bellman_ford的基础上多循环一次，用相同的条件判断如果minDist[from] > minDist[to] + value就可以说明第n次循环相较于第n - 1次minDist仍然发生了变化，那么就可以说明有负权回路

Bellman_ford队列优化版

在队列优化中，要考虑的是一种极端情况，就是当给出的图是一个双向图，也就是每一次结点都与其他n - 1个结点相连，那么当有负权回路出现的时候，就会有结点被添加到队列中第n次。所以只需要定义一个count数组记录是否有结点被添加到队列n次即可

卡玛网测试

Bellman_ford版

点击查看代码

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
    int n, m;
    cin >> n >> m;
    int s, t, v;
    vector<vector<int>> grid;
    // 图的存储
    for (int i = 0; i < m; i++) {
        cin >> s >> t >> v;
        grid.push_back({s, t, v});
    }

    vector<int> minDist(n + 1, INT_MAX);
    minDist[1] = 0;

    int ind1 = 0;
    for (int i = 0; i < n; i++) {

        for (vector<int> & side : grid) {
            int from = side[0];
            int to = side[1];
            int price = side[2];

            if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price && i < n - 1) {
                minDist[to] = minDist[from] + price;
            }
            else {
                if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) ind1 = 1;
            }
        }
    }

    if (ind1 == 1) cout << "circle" << endl;
    else if (minDist[n] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[n] << endl;
}

Bellman_ford队列优化版

点击查看代码

#include<vector>
#include<iostream>
#include<queue>
#include<climits>
#include<list>
using namespace std;

struct Edge{
    int to;
    int val;

    Edge(int t, int w): to(t), val(w) {}
};

int main() {
    int n, m;
    cin >> n >> m;
    int s, t, v;
    vector<list<Edge>> grid(n + 1);

    // 图的存储
    for (int i = 0; i < m; i++) {
        cin >> s >> t >> v;
        grid[s].push_back(Edge(t, v));
    }

    vector<int> minDist(n + 1, INT_MAX);
    minDist[1] = 0;
    queue<int> que;
    que.push(1);
    vector<bool> visited(n + 1, false);
    visited[1] = true;

    vector<int> count(n + 1, 0);
    count[1] = 1;

    while (!que.empty()) {
        int cur = que.front();
        que.pop();
        visited[cur] = false;
        for (Edge side : grid[cur]) {
            if (visited[cur] != true && minDist[side.to] > minDist[cur] + side.val && count[cur] < n) {
                minDist[side.to] = minDist[cur] + side.val;
                que.push(side.to);
                visited[cur] = false;
                count[cur]++;
            }
            else if (visited[cur] != true && minDist[side.to] > minDist[cur] + side.val && count[cur] == n) {
                cout << "circle" << endl;
                return 0;
            }
        }
    }

    if (minDist[n] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[n] << endl;
}

bellman_ford之单源有限最短路

题目描述：卡玛网96. 城市间货物运输 III
文档讲解：代码随想录(programmercarl)bellman_ford之单源有限最短路

要点

题目给定的是在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。这里多给出了两个信息，一个是不再是从城市1到城市n之间的最短路径，还有一个是最多经过k个城市。前一个信息好理解，就是后一个

如图中的结点1到结点4，中途路经两个结点，分别是2和3，那中间的边数就是3。所以如果中间至多要经过k个结点，那么就是经过k + 1条边。所以直接用Bellman_ford遍历k + 1次即可

需要注意的是，图中有负权回路，在这种情况下，上一题95只是给出了是否有负权回路的判断，但是并没有直接求最短路径的做法。所以本题要针对负权回路存在的情况进行修改，使其仍然能够输出最短路径

负权回路导致问题

在设想中，要进行k + 1遍处理，而每对所有边进行一遍松弛处理的结果就是 相当于计算起点到达与起点一条边相连的节点的最短距离

但是一旦有负权回路出现，对所有边松弛一次的结果，会成了下图这样，直接更新了起点到与起点2条，3条边相连的结点，minDist[3]和minDist[4]都被计算了，而事实上，只有minDist[2]该被计算。

而minDist[3]和minDist[4]被计算的原因就是基于minDist[2]被计算后的-1被迫更新了。

如果照这样多计算好多遍，输出的最短路径值一定是小于正常值的。

负权回路处理办法

所以要处理的就是让每一遍松弛处理只基于更新之前的minDist数值(这里得看代码理解，要不不好理解)，废话少说，放图过来！这里不得不夸一下k哥画的一手好图！

哈哈哈，开心了

下面这两张图是错误的没有经过负权处理的图

刚开始没有进行松弛处理时

minDistCopy数组进行copy就是在这里，所以在接下来对所有边的遍历中，minDistCopy数组就一直是这样了

这里是处理完结点2的时候

这里是处理完结点3的时候(实际这里不应该被计算)

代码部分

首先会定义一个minDistCopy数组，用来存储minDist更新之前的值。

for (int i = 0; i < k + 1; i++) {
	minDistCopy = minDist;
	for (vector<int> side : grid) {
		int from = side[0];
		int to = side[1];
		int val = side[2];
		if (minDistCopy[from] != INT_MAX && minDist[to] > minDist[to] > minDistCopy[from] + val)
	}
}

[1.] 首先理解这里的minDistCopy[from] != INT_MAX是说什么？为了不让结点3被计算，他之前的结点2的minDist就应该是INT_MAX才对，而minDist已经被计算过了变成了-1，所以需要回到minDistCopy
[2.] minDist[to] > minDistCopy[from] + val，还有就是这里的判断，前一个是minDist，后面又变成了minDistCopy。如果直接用minDist[to] > minDist[from] + val，那么在松弛<2, 3>的时候，就是INT_MAX > -1 + 1，所以会被直接更新。那么怎么避免？因为-2的minDist[2]已经被计算过了，但是minDistCopy[2]还是INT_MAX，那么这样INT_MAX > -1 + INT_MAX就可以了，而且这样还不会出现数值溢出

卡玛网测试

点击查看代码

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
    int n, m;
    cin >> n >> m;
    int s, t, v;
    vector<vector<int>> grid;
    // 图的存储
    for (int i = 0; i < m; i++) {
        cin >> s >> t >> v;
        grid.push_back({s, t, v});
    }

    int src, dst, k;
    cin >> src >> dst >> k;

    vector<int> minDist(n + 1, INT_MAX);
    minDist[src] = 0;
    vector<int> minDistCopy(n + 1);

    for (int i = 0; i < k + 1; i++) {
        minDistCopy = minDist;
        for (vector<int> side : grid) {
            int from = side[0];
            int to = side[1];
            int val = side[2];

            if (minDistCopy[from] != INT_MAX && minDist[to] > minDistCopy[from] + val) {
                minDist[to] = minDistCopy[from] + val;
            }
        }

        
    }

    if (minDist[dst] == INT_MAX) cout << "unreachable" << endl;
    else cout << minDist[dst] << endl;

}

posted on 2025-03-27 19:30 bnbncch 阅读(63) 评论(0) 收藏举报

刷新页面返回顶部

代码随想录算法训练营第52天|Bellman_ford 队列优化算法（又名SPFA）、bellman_ford之判断负权回路、bellman_ford之单源有限最短路

Bellman_ford 队列优化算法（又名SPFA）

梳理

卡玛网测试

bellman_ford之判断负权回路

Bellman_ford版

Bellman_ford队列优化版

卡玛网测试

Bellman_ford版

Bellman_ford队列优化版

bellman_ford之单源有限最短路

要点

负权回路导致问题

负权回路处理办法

卡玛网测试

bnbncch

公告

导航