代码随想录算法训练营第51天|dijkstra (堆优化版)、Bellman_ford 算法

dijkstra（堆优化版）

2025-03-26 18:04:09 星期三

题目描述：卡玛网47. 参加科学大会
文档讲解：代码随想录(programmercarl)dijkstra（堆优化版）精讲

优化思路

1. 在dijkstra朴素版的基础上，进行优化的核心出发点就是可能会遇到稀疏图（结点多，边少），这样在图的存储上就会浪费大量的空间

2. 在朴素版中，所有的遍历过程都是针对结点进行的，当然遇到稠密图(边数接近顶点数平方)，邻接矩阵的存储就很高效，但是一旦遇到稀疏图，那么优化空间就很大了。

所以堆优化就是站在边的角度进行的，有点kruskal的味道😄

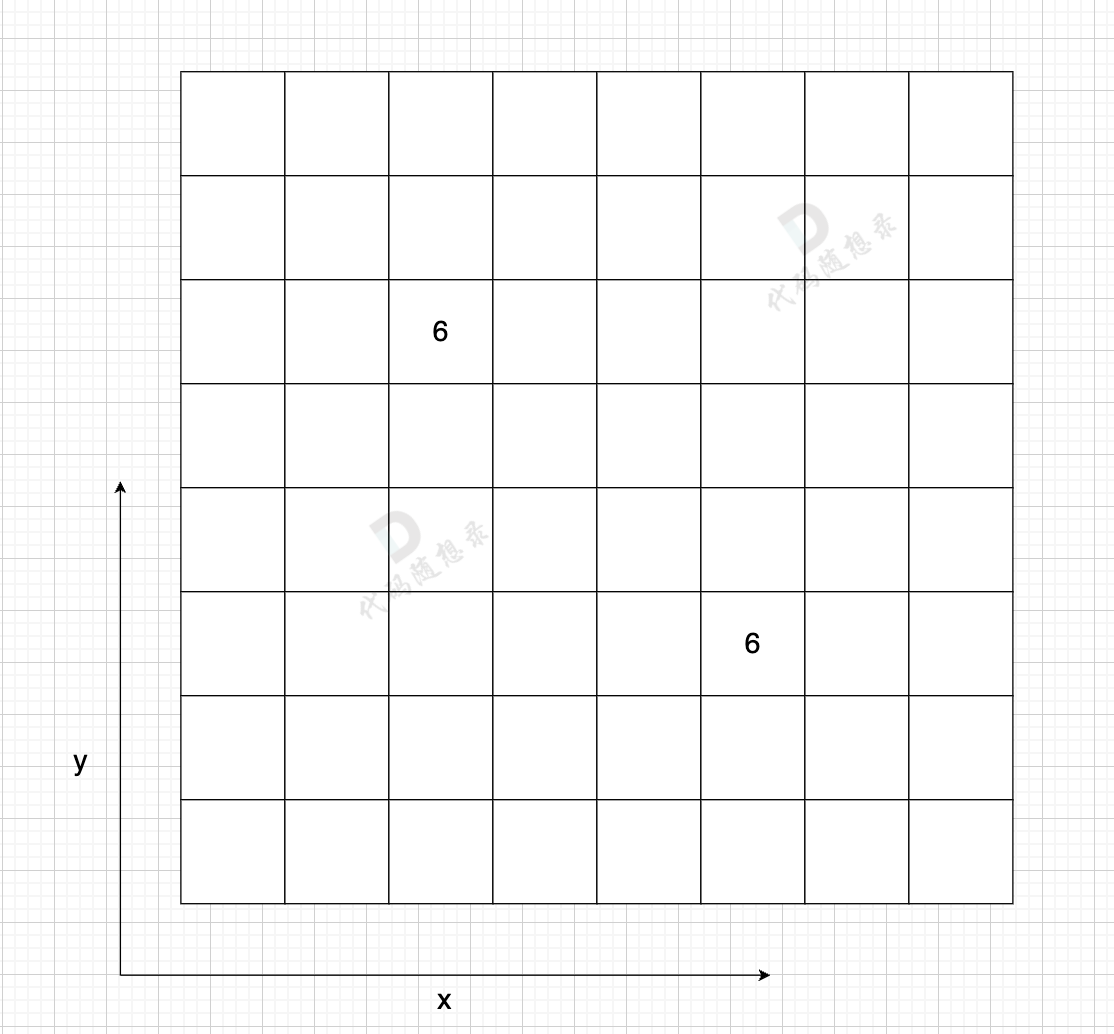
梳理

1. 如果不再用邻接矩阵，那么首先需要定义的就是一个邻接表来进行图的存储

2. 剩下的主体的三部曲不变，依然是

   1. 确定哪个未访问结点距离源点最近

   2. 将该结点标记为访问过

   3. 更新非访问结点到源点的距离(minDist数组)

3. 优化思路

   1. 但是对于第一步来说，因为要站在边的角度进行选择，就需要引入小顶堆了。因为每次dijkstra都是拿距离源点最近的边的权值进行加和，而小顶堆的最小值在堆顶，正好可以直接取出

   同时，第一步同样还需要定义minDist数组存储源点到每个结点的最短距离

   对于第二步变化不大，同样需要定义一个isVisited数组记录结点是否访问过

   对于第三步，就是照着朴素版dijkstra写就行。注意的一点是因为在邻接表存储时没有给grid赋INT_MAX，所以在比较的时候不用确定g[cur.fisrt] != INT_MAX这一步

大致代码内容

1. 注意class comparison类怎么写

---

class mycomparison {
public:
	bool operator() (const pair<int, int> &lhs, const pair<int, int> &rhs) {
		return lhs.second > rhs.second;
	}
};

2. 还有Edge结构体怎么写

   struct Edge{
   int to; // 连接到的结点
   int val; // 表示边的权值

    Edge(int t, int w) : to(t), val(w) {} // 构造函数
   

   };

3. 注意在第三步中，每次更新完minDist数组之后及时把cur.first指向的结点添加到队列中pq.push(pair<int, int>(g.to, minDist[g.to]));

卡玛网测试

这里还有一点需要注意的是if (isVisited[cur.first]) continue;，这里如果访问过了，那么就跳过

不难看出，这里的小根堆传入和进行比较的参数就是邻接表的list部分，是一个pair<int, int>，其前一个int表示指向的下一个结点，后一个int表示的两个结点之间的权值

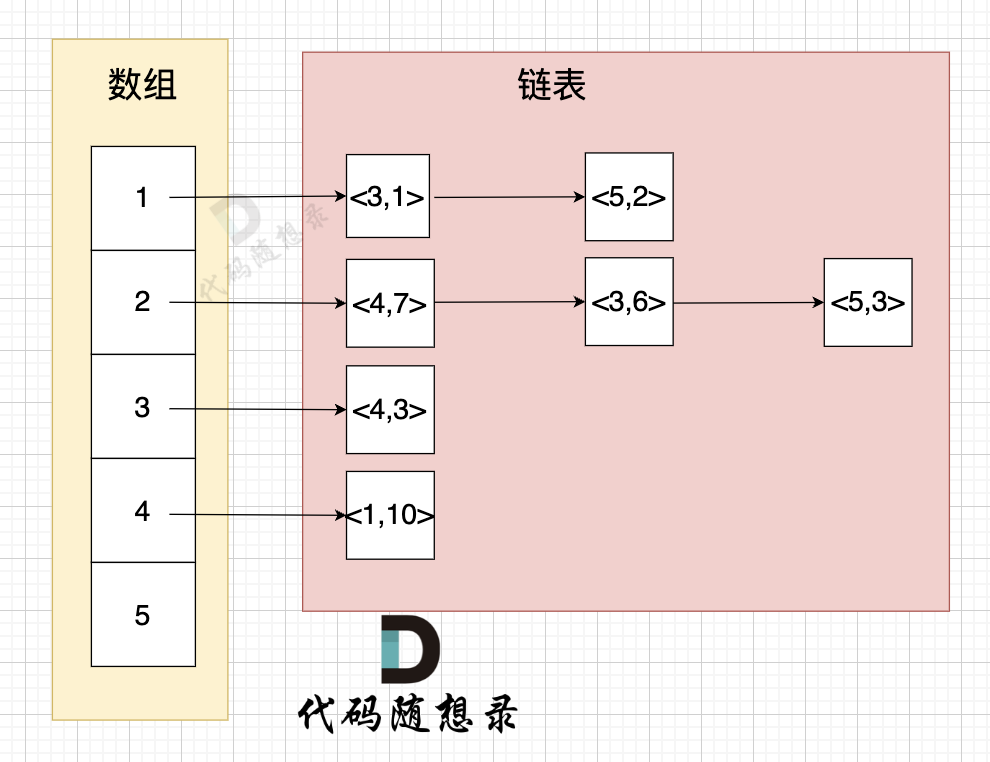
点击查看代码

#include<iostream>
#include<vector>
#include<climits>
#include<list>
#include<queue>
using namespace std;

struct Edge{
    int to; // 连接到的结点
    int val; // 表示边的权值

    Edge(int t, int w) : to(t), val(w) {} // 构造函数
};

class mycomparison {
public:
    bool operator() (const pair<int, int> &lhs, const pair<int, int> &rhs) {
        return lhs.second > rhs.second;
    }
};



int main() {
    int N, M;
    cin >> N >> M;
    int S, E, V;
    
    vector<list<Edge>> grid(N + 1);
    // 图的存储
    for (int i = 0; i < M; i++) {
        cin >> S >> E >> V;
        grid[S].push_back(Edge(E, V));
    }

    priority_queue<pair<int, int>, vector<pair<int, int>>, mycomparison> pq;

    vector<int> minDist(N + 1, INT_MAX);
    vector<bool> isVisited(N + 1, false);
    
    int start = 1;

    // 初始化优先级队列
    pq.push(pair<int, int>(start, 0));  // 这里用start方便看初始化的位置

    minDist[start] = 0;

    while (!pq.empty()) {
        // 确定源点到哪个节点近且该节点未被访问过
        pair<int, int> cur = pq.top();
        pq.pop();

        if (isVisited[cur.first]) continue;

        // 将该结点标记为访问过
        isVisited[cur.first] = true;

        // 更新未访问结点到源点的最短距离
        for (Edge g : grid[cur.first]) {
            if (!isVisited[g.to] && minDist[cur.first] + g.val < minDist[g.to]) {
                minDist[g.to] = minDist[cur.first] + g.val;
                pq.push(pair<int, int>(g.to, minDist[g.to]));
            }
        }
    }

    if (minDist[N] == INT_MAX) cout << -1 << endl;
    else cout << minDist[N] << endl;


}

Bellman_ford 算法

题目描述：94. 城市间货物运输 I
文档讲解：代码随想录(programmercarl)Bellman_ford 算法精讲

要点

1. 什么是“松弛”

   松弛是用在minDist数组里的，专门用来解决的是最短路径中出现边的权值为负数的情况。

   其核心思想有点像动态规划的递推，如果将一个有向图分解为最小单元，

   

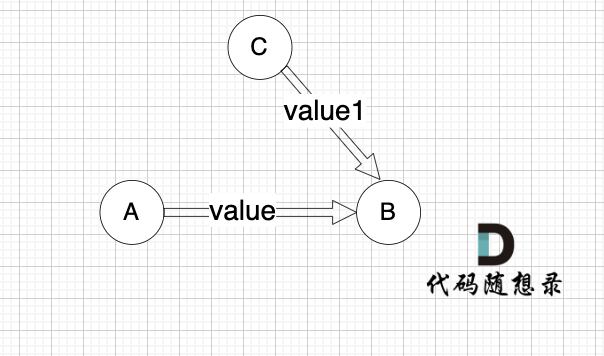
   那么此时的minDist[B]除了自身的值以外，还可以由minDist[A] + value推出来。那么他自身的值是从哪里推出来的呢？可能来源于minDist[C] + value1。而在之前dijkstra中，之所以没有计算得到真正的最短路径，就是没有将负权值的边引入minDist计算。

   所以，松弛真正的目的就是通过比大小的方式将所有的边的权值无论正负进行计算，得到最小的边，从而来更新minDist数组

   

2. 要松弛多少次才能得到单源最短路径

   将所有的边进行一次一次松弛，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。

   比如，只松弛一次，那么只能得到结点1到结点3和结点1到结点2两条边的最短路径，因为这是于起点一条边相邻的情况。当然还有与源点两条边相邻的情况，三条边相邻的情况。

   

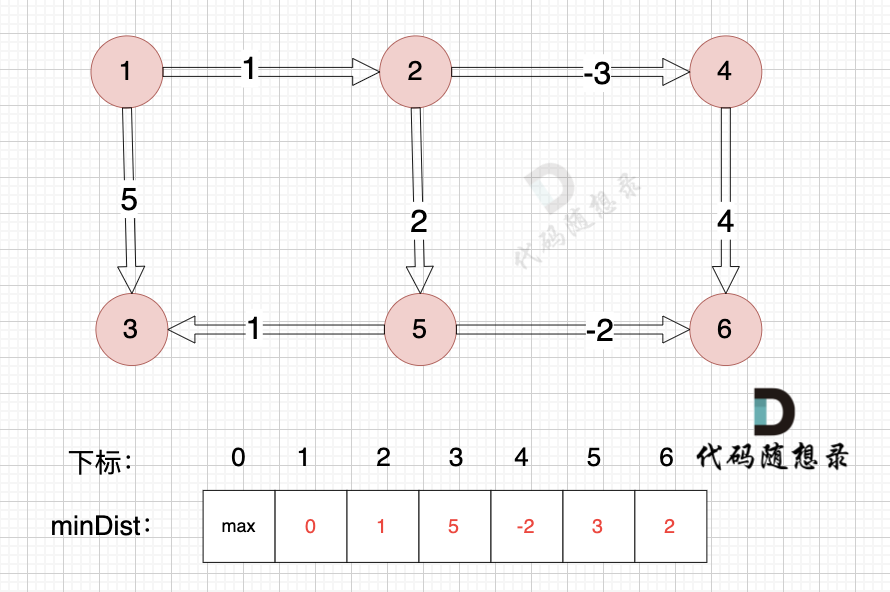
   从起点到终点，最多需要n - 1条边就可以连接起来，而如果每一边都是最短(minDist的数值最小)，那么就可以得到从1到n的最短路径了

   所以，对于一个n个结点的图，那么总共需要n - 1次就可以将图中所有的结点连接起来，所以需要进行n - 1次松弛。

梳理

1. 首先是图的存储，这里用的是朴素存储，并不是邻接矩阵

2. 之后进行循环遍历n - 1次

3. 之后用逐条遍历每条边即可堆对minDist数组进行更新即可

卡玛网测试

点击查看代码

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
    int n, m;
    cin >> n >> m;
    int s, t, v;
    vector<vector<int>> grid;
    // 图的存储
    for (int i = 0; i < m; i++) {
        cin >> s >> t >> v;
        grid.push_back({s, t, v});
    }

    vector<int> minDist(n + 1, INT_MAX);
    minDist[1] = 0;

    for (int i = 0; i < n - 1; i++) {

        for (vector<int> & side : grid) {
            int from = side[0];
            int to = side[1];
            int price = side[2];

            if (minDist[from] != INT_MAX && minDist[to] > minDist[from] + price) {
                minDist[to] = minDist[from] + price;
            }
        }
    }

    if (minDist[n] == INT_MAX) cout << "unconnected" << endl;
    else cout << minDist[n] << endl;
}