代码随想录算法训练营第50天|拓扑排序、dijkstra（朴素版）

拓扑排序

2025-03-25 20:47:35 星期二

题目描述：卡玛网117. 软件构建
文档讲解：代码随想录(programmercarl)拓扑排序精讲

问题描述

1. 拓扑排序的应用场景

1. 大学排课，例如 先上A课，才能上B课，上了B课才能上C课，上了A课才能上D课，等等一系列这样的依赖顺序

2. 做项目安装文件包的时候，经常发现 复杂的文件依赖关系， A依赖B，B依赖C，B依赖D，C依赖E 等等。

就像这样要给出一条线性的依赖顺序。

给出一个有向图，把这个有向图转成线性的排序就叫拓扑排序

2. 检测有向图是否有环

   如果图中存在循环依赖，那么就不能做线性排序了，所以拓扑排序也是判断有向无环图的常用方法

3. 实现拓扑排序有两种方式，BFS和DFS算法，BFS清晰易懂

注：上面摘自代码随想录文档

拓扑排序过程梳理

1. 找到入度为0的结点，只有入度为0，它才是出发节点。之后加入结果集

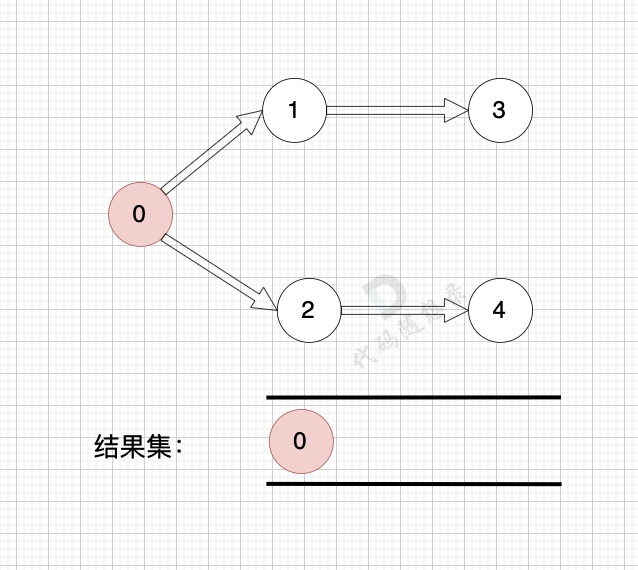
2. 将该点从图中删除

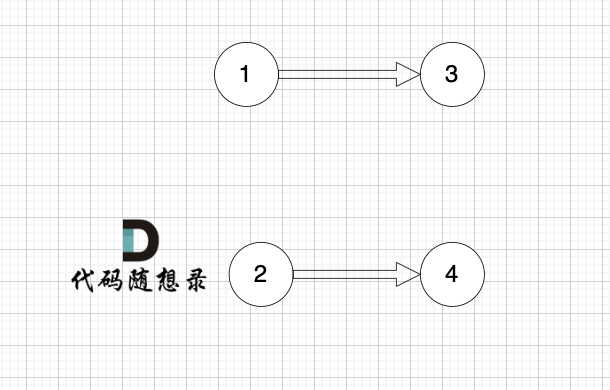
循环以上两步，直到 所有节点都在图中被移除了。

结果集的顺序，就是我们想要的拓扑排序顺序 （结果集里顺序可能不唯一）

大致代码内容

1. 图的存储。

   首先要对图中所有结点的入度进行统计，定义一个一维数组inDegree用来存储。同时还需要记录文件之间的依赖关系，这里需要定义一个二维的map结构进行存储unordered_map<int, vector<int>> umap;

2. 定义一个结果集result，将入度为0的结点加入到结果集，同时需要将该结点从图中删除。如何进行删除，就是将图中该结点出发的结点的入度减1

   这里有个问题就是因为每次入度为0的结点不是只有一个，所以需要一次性加入到result中的结点不止一个，但是因为对每一个入度为的0结点要在umap中将其指向的结点入度-1，所以不能直接将入度为0的结点加入到result中，而是需要一个中间步骤，对每一个入度为0的结点进行单独处理。所以，这里引入了队列，当然BFS的数据结构也可以用栈，数组等。

3. 需要注意的是，最后的result的size()如果不等于输入的结点个数，那么就说明图中有环，输出-1即可

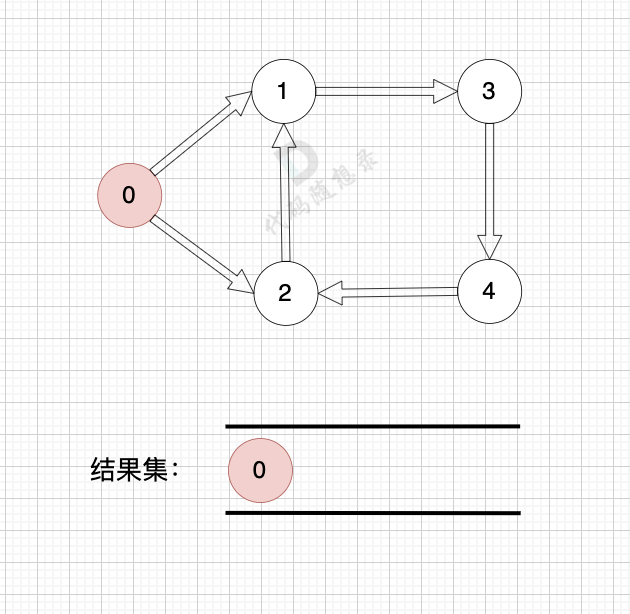
卡玛网测试

点击查看代码

#include<iostream>
#include<vector>
#include<unordered_map>
#include<queue>
using namespace std;
int main() {
    int N, M;
    cin >> N >> M;
    int S, T;
    unordered_map<int, vector<int>> umap;
    vector<int> inDegree(N, 0);
    // 图的存储
    for (int i = 0; i < M; i++) {
        cin >> S >> T;
        inDegree[T]++;
        umap[S].push_back(T);
    }

    vector<int> result;
    queue<int> que;


    // 先将入度为0的所有结点加入队列
    for (int i = 0; i < N; i++) {
        if (inDegree[i] == 0) {
            que.push(i);
        }
    }

    // 对所有入度为0的结点进行中间处理，即入度-1
    while (!que.empty()) {
        int cur;
        cur = que.front();
        que.pop();
        result.push_back(cur);
        if (umap[cur].size() > 0) {
            for (int u : umap[cur]) {
                inDegree[u]--;
                if (inDegree[u] == 0) que.push(u);
            }
        }
        
    }

    if (result.size() != N) {
        cout << -1 << endl;
        return 0;
    }


    for (int i = 0; i < result.size(); i++) {
        if (i != result.size() - 1) cout << result[i] << " ";
        else cout << result[i];
    }
    
}

dijkstra（朴素版）

题目描述：卡玛网47. 参加科学大会
文档讲解：代码随想录(programmercarl)dijkstra（朴素版）精讲

朴素版dijkstra三部曲梳理

dijkstra是处理边的权值非负的最短路算法

这里和prim三部曲是很像的，区别就在prim三部曲更新的是非最小生成树到最小生成树的距离，dijkstra更新的是未访问结点到源点之间的距离

1. 选源点到哪个结点近且该结点未被访问过

2. 将该结点标记为访问过

3. 更新非访问结点到源点的距离(更新minDist数组)

大致代码内容

1. 首先定义一个一维数组grid用来存储有向图每条边的权值，之后定义一个一位数组minDist用来表示非访问结点到源点的最小距离

2. 之后定义一个bool类型的isVisited数组用来标记节点是否被访问过

3. 更新非访问结点到源点的距离，这里和prim不同的的地方就在于最后需要更新的是未访问结点到源点之间的最小距离，那么除了grid[cur][j]表示未访问结点到最新标记过的结点之间的距离外，还需要多加上这个最新被标记过结点的minDist值。也就是if (grid[cur][j] + minDist[cur] < minDist[j]) minDist[j] = grid[cur][j] + minDist[cur];

卡玛网测试

同时这里有两点需要注意

1. 起始点到自身的距离应该是0，minDist[1] = 0; 。这样才能做更新

2. 47和之前53寻宝不同的地方在于，53给出了边的权值最大不超过10000，而本题并没有给出最大的权值。那么在初始化grid数组的时候就只能全赋成INT_MAX。

   但是这样有一个问题就是在第一次确定源点距离哪个未访问结点最近时，同时比较的是两个INT_MAX，那么cur就不会被更新(minDist[1]是0已经可以被更新了)。所以此时默认是对结点1进行处理的，那么处理办法就是给cur直接赋成初值为1即可，不要像之前的prim赋成-1

3. 在处理第三步更新非访问结点到源点之间的距离时，要注意多加一个grid[cur][j] != INT_MAX的判断，因为尽量要避免最大值和别的数相加，这样会导致整数溢出

4. 在最开始的那个大循环里，之前prim用的是N - 1次循环，构建N - 1条边，来求出边的最小总和。但是dijkstra是站在结点的角度去考虑的，也就是循环N次将所有的结点都添加一遍。

有了前面prim的基础，dijkstra就好很多了。

点击查看代码

#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
    int N, M;
    cin >> N >> M;
    int S, E, V;
    // 图的存储
    vector<vector<int>> grid(N + 1, vector<int>(N + 1, INT_MAX));
    vector<int> minDist(N + 1, INT_MAX);
    minDist[1] = 0;
    for (int i = 0; i < M; i++) {
        cin >> S >> E >> V;
        grid[S][E] = V;
    }

    vector<bool> isVisited(N + 1, false);
    for (int i = 0; i < N; i++) {
        int minVal = INT_MAX;
        int cur = 1;
        // 选源点到哪个结点近且该节点未被访问过
        for (int j = 1; j <= N; j++) {
            if (!isVisited[j] && minDist[j] < minVal) {
                minVal = minDist[j];
                cur = j;
            }
        }

        // 将该节点标记为访问过
        isVisited[cur] = true;

        // 更新非访问结点到源点之间的距离
        for (int j = 1; j <= N; j++) {
            if (!isVisited[j] && grid[cur][j] != INT_MAX && grid[cur][j] + minDist[cur] < minDist[j]) {
                minDist[j] = grid[cur][j] + minDist[cur];
            }
        }
    }

    if (minDist[N] == INT_MAX) cout << -1 << endl;
    else cout << minDist[N] << endl;
        

}