代码随想录算法训练营第49天|最小生成树之prim、最小生成树之kruskal
最小生成树之prim
2025-03-25 14:31:20 星期二
题目描述:卡玛网53
文档讲解:代码随想录(programmercarl)最小生成树之prim
最小生成树是所有结点的最小连通子图,即:以最小的成本将图中所有的结点连在一起。
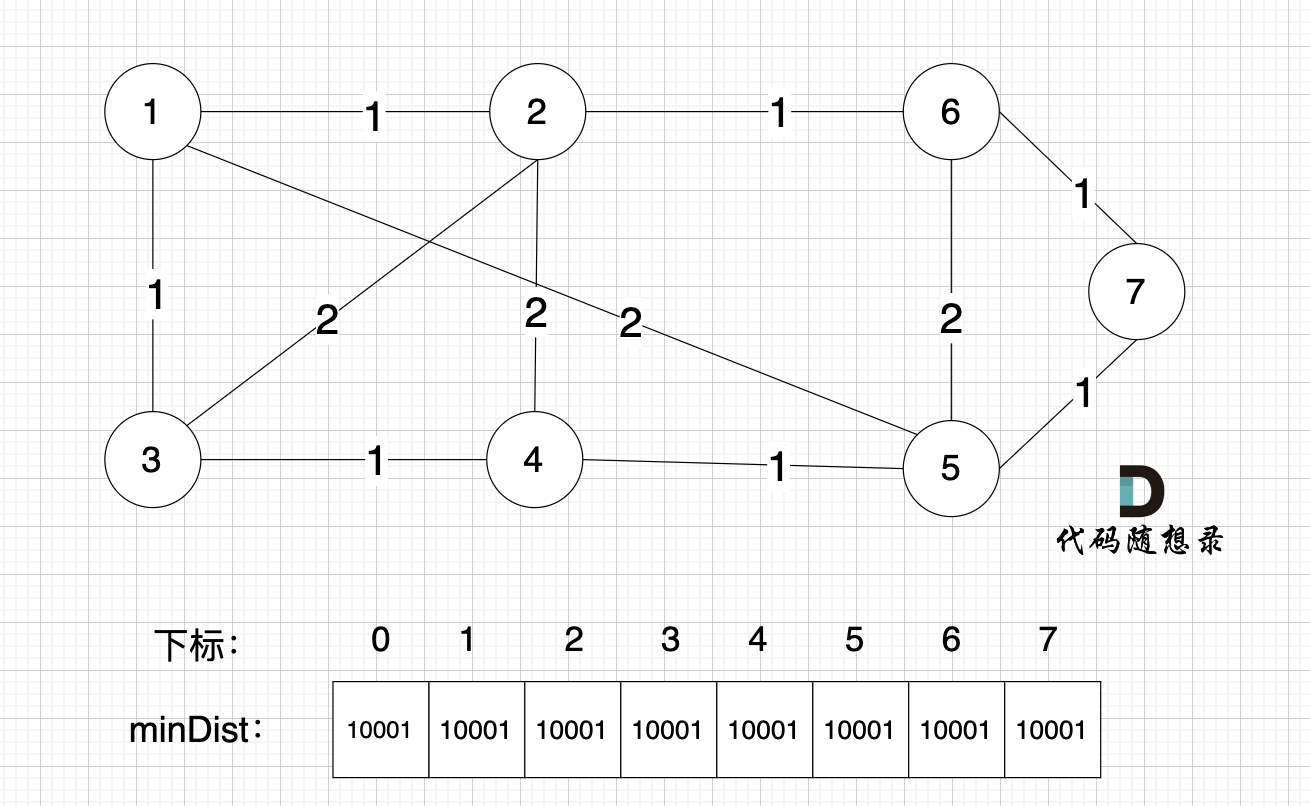
而prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。拿生成树是一颗树,有好多结点,那么如何判断最近的结点是和生成树中那个结点最近的呢?这里就要用到了minDist数组
minDist数组用来记录每一个节点距离最小生成树的最近距离
接下俩就是prim三部曲
梳理
-
确定离最小生成树最近的结点。
-
将最近结点加入最小生成树
-
更新非生成树到生成树的距离
大致代码内容
注:v代表结点的数量
-
在prim算法中,首先定义一个一维数组
vector<int> isInTree(v + 1, false)用来记录这个结点是否在树中,同时定义一个一维数组vector<int> minDist(v + 1, 10001)用来存储结点到最小生成树的距离 -
确定离最小生成树最近的结点。
这里为什么从1开始到小于等于v结束,表示结点的标号
int cur = -1;//表示当前结点
int minVal = INT_MAX;
for (int j = 1; j <= v; j++) {
if (!isInTree && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
-
最近结点加入生成树。直接用
isInTree[cur] = True;即可 -
更新非生成树到生成树之间的距离
for (int j = 1; j <= v; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
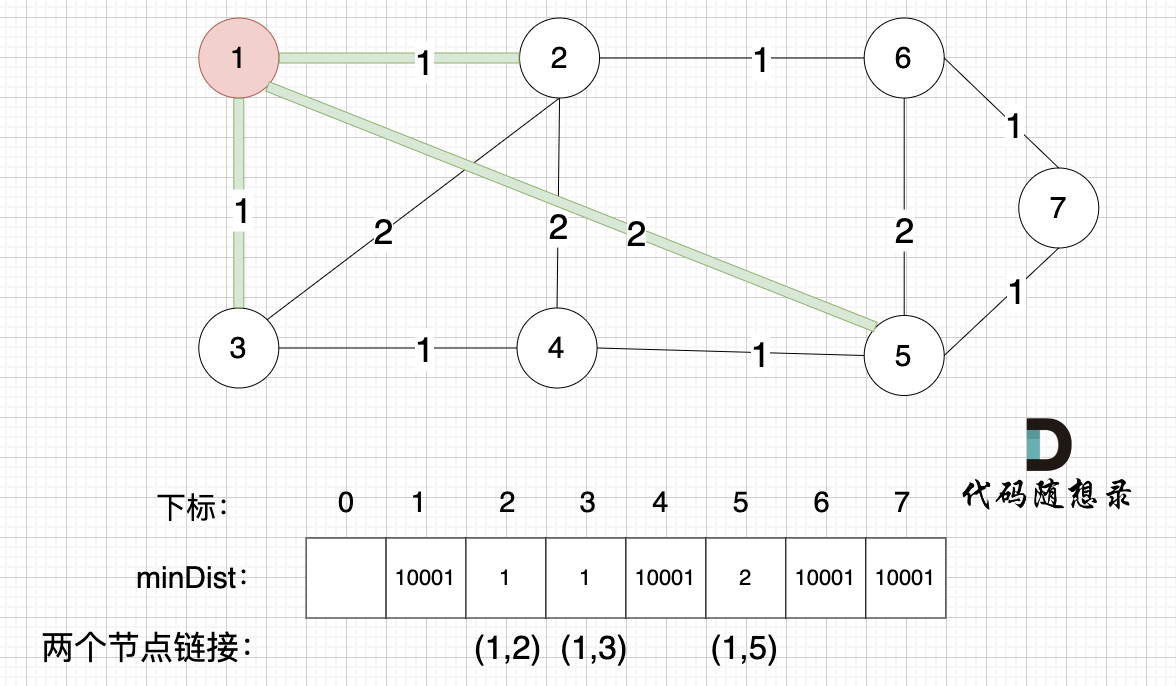
- 上面的部分每次只能添加一个结点到最小生成树中,理应来说应该是循环v次。但对于一个v个结点的图来说,一定可以用v - 1条边将所有的结点连接起来,而最小生成树求得是边的最短长度,那么就应该是循环v - 1次来添加v - 1条边即可
卡玛网测试
一直有一个错误找不到,找了半天,真的是半天,代码重写了一遍,问了GPT(说的错的),最后我说一行一行对把......第一行初始化grid写错了😵😵
vector<vector<int>> grid(V + 1, vector<int>(V + 1, 0));刚开始习惯性地全写成0了,我说怎么最后result加半天是0,grid全是0,直接给minDist全赋成0了,最后可不全是0吗
vector<vector<int>> grid(V + 1, vector<int>(V + 1, 10001));初始成10001就行了
点击查看代码
#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
int V, E;
cin >> V >> E;
int v1, v2, val;
vector<vector<int>> grid(V + 1, vector<int>(V + 1, 10001));
for (int i = 0; i < E; i++) {
cin >> v1 >> v2 >> val;
grid[v1][v2] = val;
grid[v2][v1] = val;
}
vector<int> minDist(V + 1, 10001);
vector<bool> isInTree(V + 1, false);
for (int i = 1; i < V; i++) {
int minVal = INT_MAX;
int cur = -1;
// 确定离最小生成树最近的结点。
for (int j = 1; j <= V; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 将最近结点加入最小生成树
isInTree[cur] = true;
// 更新非生成树到生成树的距离
for (int j = 1; j <= V; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
}
}
}
int result = 0;
for (int i = 2; i <= V; i++) {
result += minDist[i];
}
cout << result << endl;
}
输出边的连接情况
如果要将边的连接情况进行输出,那么就需要一个数组来存储最小生成树某条边的两个点,这里用一维数组,parent[i] = j,则表示i和j相连
而minDist数组里记录的是最小生成树的边的权值,那么minDist数组记录了最小生成树的边,所以用parent数组来记录最小生成树的边要在prim三部曲的第三步中进行记录

点击查看代码
#include<iostream>
#include<vector>
#include<climits>
using namespace std;
int main() {
int V, E;
cin >> V >> E;
int v1, v2, val;
vector<vector<int>> grid(V + 1, vector<int>(V + 1, 10001));
for (int i = 0; i < E; i++) {
cin >> v1 >> v2 >> val;
grid[v1][v2] = val;
grid[v2][v1] = val;
}
vector<int> minDist(V + 1, 10001);
vector<bool> isInTree(V + 1, false);
vector<int> parent(V + 1, 0);
for (int i = 1; i < V; i++) {
int minVal = INT_MAX;
int cur = -1;
// 确定离最小生成树最近的结点。
for (int j = 1; j <= V; j++) {
if (!isInTree[j] && minDist[j] < minVal) {
minVal = minDist[j];
cur = j;
}
}
// 将最近结点加入最小生成树
isInTree[cur] = true;
// 更新非生成树到生成树的距离
for (int j = 1; j <= V; j++) {
if (!isInTree[j] && grid[cur][j] < minDist[j]) {
minDist[j] = grid[cur][j];
parent[j] = cur;
}
}
}
// int result = 0;
// for (int i = 2; i <= V; i++) {
// result += minDist[i];
// }
// cout << result << endl;
for (int i = 1; i <= V; i++) {
cout << i << "->" << parent[i] << endl;
}
}
最小生成树之kruskal
题目描述:卡玛网53
文档讲解:代码随想录(programmercarl)最小生成树之kruskal
kruskal的思路
-
按照边的权值排序,优先选择小的边加入到生成树中
-
遍历排序后的边
-
如果边首尾的两个结点在一个集合中,那么不做处理
-
如果不在一个集合中,那么加入到最小生成树中,把两个结点加入到同一个集合中
-
这里核心的问题就是判断两个结点是不是在同一个集合,那么就需要用到并查集
大致代码内容
- 这里需要对边的权值进行排序,需要定义一个新的结构用来存储两条边和一个权值
struct Edge {
int l, r, val;
};
之后使用快排进行排序
sort(edges.begin(), edges.end(), [](const Edge &a, const Edge &b)) {
rerurn a.val < b.val;
}
- 后面的部分并不需要"加入到最小生成树"的操作,直接判断同一条边上的两个结点是否在同一个结点上即可。当然了,如果需要输出最小生成树的边,那么则需要将边添加到最小生成树中,这里用数组进行表示
卡玛网测试
还有就是注意初始化的部分,如果不初始化,数组就会越界
点击查看代码
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int V;
vector<int> father(V + 1, 0);
struct Edge{
int l, r, val;
};
void init () {
for (int i = 1; i <= V; i++) father[i] = i;
}
int find(int u) {
if (u == father[u]) return u;
else return father[u] = find(father[u]);
}
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return (u == v);
}
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
father[v] = u;
}
int main() {
int E;
cin >> V >> E;
int v1, v2, val;
vector<Edge> edges;
for (int i = 0; i < E; i++) {
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
sort(edges.begin(), edges.end(), [](const Edge &a, const Edge &b) { return a.val < b.val;});
init();
int result = 0;
for (int i = 0; i < E; i++) {
if (!isSame(edges[i].l, edges[i].r)) {
result += edges[i].val;
join(edges[i].l, edges[i].r);
}
}
cout << result << endl;
}
输出边的连接情况
输出边的连接情况直接新建一个Edge结构体进行边的存储即可

点击查看代码
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int V;
vector<int> father(V + 1, 0);
struct Edge{
int l, r, val;
};
void init () {
for (int i = 1; i <= V; i++) father[i] = i;
}
int find(int u) {
if (u == father[u]) return u;
else return father[u] = find(father[u]);
}
bool isSame(int u, int v) {
u = find(u);
v = find(v);
return (u == v);
}
void join(int u, int v) {
u = find(u);
v = find(v);
if (u == v) return;
father[v] = u;
}
int main() {
int E;
cin >> V >> E;
int v1, v2, val;
vector<Edge> edges;
for (int i = 0; i < E; i++) {
cin >> v1 >> v2 >> val;
edges.push_back({v1, v2, val});
}
sort(edges.begin(), edges.end(), [](const Edge &a, const Edge &b) { return a.val < b.val;});
init();
vector<Edge> result;
for (int i = 0; i < E; i++) {
if (!isSame(edges[i].l, edges[i].r)) {
join(edges[i].l, edges[i].r);
result.push_back({edges[i].l, edges[i].r, edges[i].val});
}
}
for (Edge re : result) {
cout << re.l << " : " << re.r << " -> " << re.val << endl;
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号