代码随想录算法训练营第48天|108. 冗余连接、109. 冗余连接II

卡玛网108

2025-03-24 13:19:04 星期一

题目描述：卡玛网108
文档讲解：代码随想录(programmercarl)108. 冗余连接

这个题思路比较简单，核心就是如果两个结点通过isSame函数出现在同一个集合中，那么说明二者已经连接到同一个父节点下了，那么此时再添加一条二者的边，就直接输出这条边即可。反之，如果没有出现在同一个集合，那么将其添加到同一个集合中。

卡玛网测试

点击查看代码

#include<iostream>
#include<vector>
using namespace std;
int N;
vector<int> father(1001, 0);

void init() {
    for (int i = 1; i <= N; i++) father[i] = i;
}

int find(int u) {
    if (u == father[u]) return u;
    else return father[u] = find(father[u]);
}

bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return (u == v);
}

void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return;
    father[v] = u;
}

int main() {
    cin >> N;
    init();
    int s, t;
    for (int i = 0; i < N; i++) {
        cin >> s >> t;
        if (isSame(s, t)) {
            cout << s << ' ' << t << endl;
            return 0;
        }
        else join(s, t);   
    }
}

卡玛网109

题目描述：卡玛网109
文档讲解：代码随想录(programmercarl)109. 冗余连接II

有向树的定义：只有根节点入度为0，其他节点入度都为1（因为该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点）

本题的目的是将有向图删除一条边后使其变成一颗有向树

三种情况

1. 情况一：找到入度为2的点，其中两条边都可以删掉，那么删除其中一条指向该结点的边即可(但是因为需要倒序，所以只能删除后输入的一条）

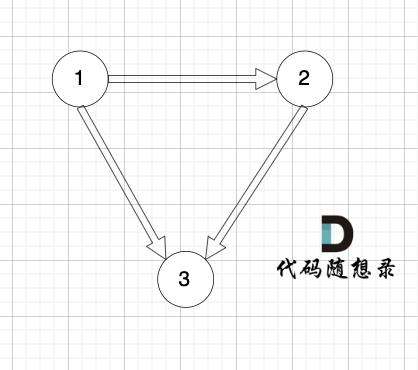
2. 情况二：找到入度为2的点，只能删除一条特定的边。因为其中一条边被删除之后会形成环

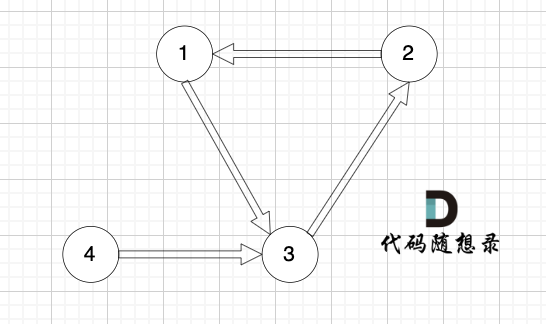
3. 情况三：没有入度为二的点，说明图中有环了。那么删除构成环的边即可

梳理

1. 统计所有结点的入度

   这里需要引入一个vector<int> inDegree来记录每一个结点的入度。同时还需要有一个二维edges数组来添加每一条边。

   同时再通过一个for循环对edges中入度为2的结点进行查找，并将其指向入度为2结点的点添加到另一个一维数组vec中。

   注意：这里的vec是一个一维数组，其表示的是int型的点，比如[2, 1]和[3, 1]，入度为2的点是1，那么添加到vec数组中的就是[2, 3]。于是我们表示这条有向边的时候，就用edges[vec[0]][0]和edges[vec[0]][1]来进行表示

2. 如果vec.size() > 0，也就是确定vec中存放了入度为2结点的边，那么对入度为2的结点的边进行删除。如果删除掉任意一条边都可以构成一颗有向树，那么需要从后面开始进行删除。但是，如果情况二，即使他是后面添加进来的边，但是删除之后勾陈了一个环，那么仍然是不能构成一颗有向树，所以到底要删除哪一条边，还需要引入一个isTreeAfterRemoveEdge()函数来判断删除其中一条边之后是否是一颗有向树，这里还有并查集即可

   这里定义一个getRemoveEdge函数，进行边的删除。传入的参数就是上面定义的edges二维数组。

3. 如果没有入度的话，那么直接按照顺序将两个结点依次加入并查集，一旦出现两个相同的结点，那么就输出该边即可

卡玛网测试

这个题感觉很不好写，还有好多小细节需要处理

1. 在新建edges数组的时候，不能像这样一样赋初值vector<vector<int>> edges(N, vector<int>(N, 0));，因为edges数组并没有从1开始进行计数的说法，所以直接赋N。但是这样后面在进行push_back的时候，会在0的基础上继续push_back这样的情况。

   举个例子，比如N = 2，那么后面的值就是这样[{0, 0},{0, 0}, {1, 2}, {3, 4}]，({1, 2}, {3, 4}仅用作举例)本来edges的大小为2，这么一搞就会数组越界。所以一开始就不要进行赋初值

2. 由于edges的数组是push_back的，所以在isTreeAfterRemoveEdge函数中进行if (i != deleteEdge) 比较的时候，二者的类型必须是一样的。这里都表示的是下标索引，而不是edges[i][0]的具体某个值。

   为什么会说到这里，因为这样同样会导致数组越界。isTreeAfterRemoveEdge函数中下标i一定不能等于edges.size()。那么同样在传deleteEdge参数，也就是vec[0]，也只能是一个小于edges.size()的索引，所以就不能不是具体的edges[i][0]。刚开始这里就写错了

---

// 情况一和情况二
// 注意优先从后面添加的边进行删除
if (vec.size() > 0) {
	if (isTreeAfterRemoveEdge(edges, vec[0])) {
		cout << edges[vec[0]][0] << ' ' << edges[vec[0]][1] << endl;;
		return 0;
	}
	cout << edges[vec[1]][0] << ' ' << edges[vec[1]][1] << endl;;
	return 0;
}

点击查看代码

#include<iostream>
#include<vector>
using namespace std;
int N;
vector<int> father(1001, 0);

void init() {
    for (int i = 1; i <= N; i++) father[i] = i;
}

int find(int u) {
    if (u == father[u]) return u;
    else return father[u] = find(father[u]);
}

bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return (u == v);
}

void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return;
    father[v] = u;
}

bool isTreeAfterRemoveEdge(vector<vector<int>> &edges, int deleteEdge) {
    for (int i = 0; i < edges.size(); i++) {
        if (i != deleteEdge) {
            if (isSame(edges[i][0], edges[i][1])) return false;
            join(edges[i][0], edges[i][1]);
        }
    }
    return true;
}

int main() {
    cin >> N;
    init();
    int s, t;
    vector<vector<int>> edges;
    vector<int> inDegree(N + 1, 0);
    // 图的存储
    for (int i = 0; i < N; i++) {
        cin >> s >> t;
        inDegree[t]++;
        edges.push_back({s, t});
    }


    // 找到每一个入度为2的边的索引
    vector<int> vec;
    for (int i = N - 1; i >= 0; i--) {
        
        if (inDegree[edges[i][1]] == 2) {
            vec.push_back(i);
        } 
    }


    // 情况一和情况二
    // 注意优先从后面添加的边进行删除
    if (vec.size() > 0) {
        if (isTreeAfterRemoveEdge(edges, vec[0])) {
            cout << edges[vec[0]][0] << ' ' << edges[vec[0]][1] << endl;;
            return 0;
        }
        cout << edges[vec[1]][0] << ' ' << edges[vec[1]][1] << endl;;
        return 0;
    }

    // 情况三
    
    for (int i = 0; i < edges.size(); i++) {
        if (isSame(edges[i][0], edges[i][1])) {
            cout << edges[i][0] << ' ' << edges[i][1] << endl;
        }
        join(edges[i][0], edges[i][1]);
    }
}