代码随想录算法训练营第47天|并查集理论基础、107. 寻找存在的路径

并查集理论基础

2025-03-22 16:31:43 星期六

文档讲解：代码随想录(programmercarl)并查集理论基础

梳理

1. 并查集主要解决什么问题呢？

   并查集常用来解决连通性问题。就是当需要判断两个元素是否在同一个集合的时候，就需要用到并查集

2. 并查集的功能

   1. 将两个元素添加到一个集合中

   2. 判断两个元素在不在同一个集合

3. 其实并查集的两个功能之间是想相通的，将两个元素添加到一个集合中，那么两个元素自然就是在同一个集合了。所以并查集的核心就是要明白并查集的寻根思路。这里的做法就是设置一个“根”，比如A和B两个元素，只要A的根是B，然后B的根就是自己，那么就说明两个元素具有相同的根，那么就可以表示两个元素在同一个集合中。

   

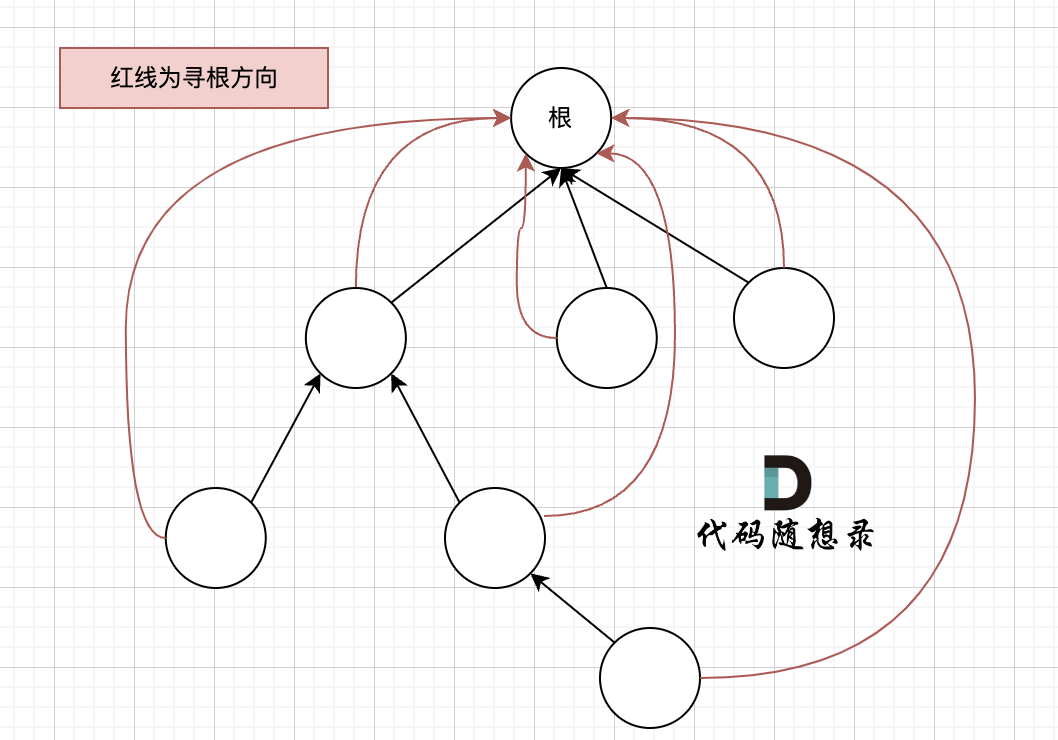
   看上面的图，只要所有的结点的根都是一样的，那么就表示这些结点都在同一个集合中

   当然了，如果这棵多叉树高度很深的话，每次寻根又都是一个递归的过程，那么寻找根就要递归很多次。所以引入了状态压缩

   

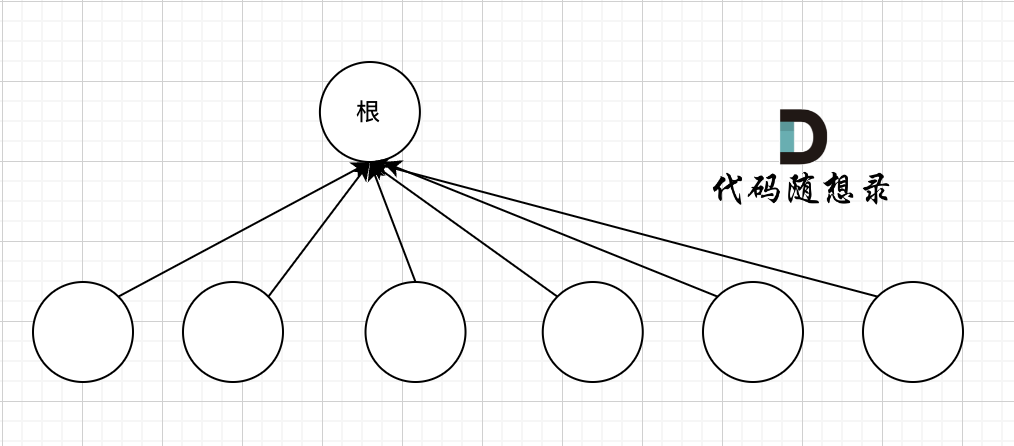
   我们的目的只需要知道这些节点在同一个根下就可以，所以对这棵多叉树的构造只需要这样(k哥原话)

   状态压缩核心的变化就是下面代码中的find函数中，将结点u的根father[u]承接住递归的值即可

并查集代码模板

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

// 初始化并查集
void init() {
	for (int i = 1; i <= n; i++) father[i] = i;
}

// 并查集寻根
int find(int u) {
	if (u == father[u]) return u;
	else return father[u] = find(father[u]);
}

// 判断u和v是否找到同一个根
bool isSame(int u, int v) {
	u = find(u);
	v = find(v);
	return (u == v);
}

// 将v->u这条边加入并查集
void join(int u, int v) {
	u = find(u);
	v = find(v);
	if (u == v) return;
	father[v] = u;
}

卡玛网107

题目描述：卡玛网107
文档讲解：代码随想录(programmercarl)107. 寻找存在的路径

卡玛网测试

注意，在写并查集寻根的时候else的部分忘记return了，刚开始一致报数组越界，哪里也找不到

剩下本题的代码套用上面的模板直接就可以过了，比较简单。今天是放水的一天哈哈哈哈😁

点击查看代码

#include<iostream>
#include<vector>
using namespace std;
int N;
vector<int> father(101, 0);

// 初始化并查集
void init() {
    for (int i = 1; i <= N; i++) father[i] = i;
}

// 并查集寻根
int find(int u) {
    if (u == father[u]) return u;
    else return father[u] = find(father[u]);
}

// 判断u和v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return (u == v);
}

// 将v->u这条边加入并查集
void join(int u, int v) {
    u = find(u);
    v = find(v);
    if (u == v) return;
    father[v] = u;
}

int main() {
    int M;
    cin >> N >> M;
    init();
    int s, t;
    // 图的存储
    for (int i = 0; i < M; i++) {
        cin >> s >> t;
        // 并查集存储
        join(s, t);
    }

    cin >> s >> t;
    if (isSame(s, t)) {
        cout << 1 << endl;
        return 0;
    }
    else cout << 0 << endl;

}