代码随想录算法训练营第46天|106. 岛屿的周长、110. 字符串接龙、105.有向图的完全可达性
卡玛网106
2025-03-21 19:12:25 星期五
题目描述:卡玛网106
文档讲解:代码随想录(programmercarl)106. 岛屿的周长
梳理
-
首先是需要遍历每一个图中的岛屿(也就是1)
-
对每一个为1的岛屿遍历其四周是否有海洋或者与边界连接(这种情况也算)
-
最后返回count
卡玛网测试
这里其实本题有几个坑需要记录一下
-
刚看了一下文档讲解,首先第一个本题k哥说是为了避免惯性思维,其实压根用不着dfs或者bfs,结果还是用了dfs
-
就是在深搜的函数中,写的calPerimeter函数(这个其实是从104来的思路)是对nextx和nexty计算的,结果结果一直不对,后来把所有的点打印出来对照看了一下,发现才是没有对第一个点(陆地)的周边进行统计,如下图
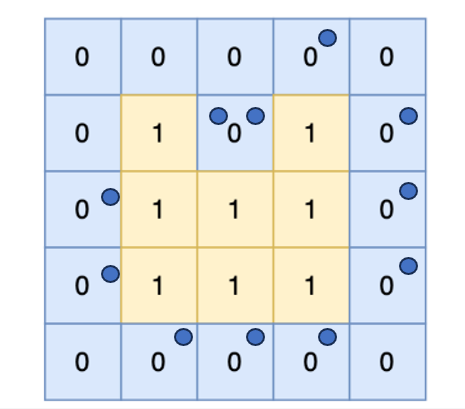
- 另外一个坑就是属于没有想到的,就是像这种挨着边界的陆地,我一开始在calPerimeter是没有做判断的,也就是边界情况也需要进行count++。
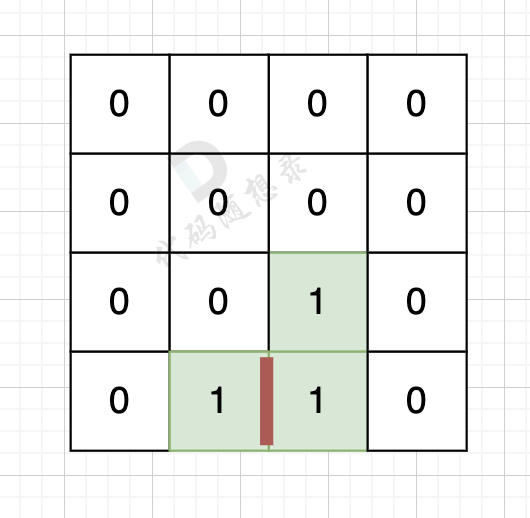
同时,在进行判断的时候需要注意,这里需要加一个else if的判断,否则grid[nearx][neary]会出现数组越界的情况。
if (nearx < 0 || nearx >= grid.size() || neary < 0 || neary >= grid[0].size()) count++;
else if (grid[nearx][neary] == 0) {
// cout << nearx << ' ' << neary << endl;
count++;
}
dfs代码
这个其实完全没必要,下面的精简版就是直接删了dfs的
点击查看代码
#include<iostream>
#include<vector>
using namespace std;
int count = 0;
int dir[4][2] = {1, 0, 0, 1, -1, 0, 0, -1};
void calPerimeter(vector<vector<int>> &grid, vector<vector<int>> &visited, int x, int y) {
for (int i = 0; i < 4; i++) {
int nearx = x + dir[i][0];
int neary = y + dir[i][1];
if (nearx < 0 || nearx >= grid.size() || neary < 0 || neary >= grid[0].size()) count++;
else if (grid[nearx][neary] == 0) {
// cout << nearx << ' ' << neary << endl;
count++;
}
}
}
void dfs(vector<vector<int>> &grid, vector<vector<int>> &visited, int x, int y) {
if (grid[x][y] == 0 || visited[x][y] == 1) return;
visited[x][y] = 1;
calPerimeter(grid, visited, x, y);
for (int i = 0; i < 4; i++) {
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;
if (grid[nextx][nexty] == 1 && visited[nextx][nexty] == 0) {
// calPerimeter(grid, visited, nextx, nexty);
dfs(grid, visited, nextx, nexty);
}
}
}
int main() {
int N, M;
cin >> N >> M;
vector<vector<int>> grid(N, vector<int>(M, 0));
vector<vector<int>> visited(N, vector<int>(M, 0));
// 图的存储
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
cin >> grid[i][j];
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (grid[i][j] == 1 && visited[i][j] == 0) {
dfs(grid, visited, i, j);
}
}
}
cout << count << endl;
}
精简版本代码
点击查看代码
#include<iostream>
#include<vector>
using namespace std;
int count = 0;
int dir[4][2] = {1, 0, 0, 1, -1, 0, 0, -1};
void calPerimeter(vector<vector<int>> &grid, int x, int y) {
for (int i = 0; i < 4; i++) {
int nearx = x + dir[i][0];
int neary = y + dir[i][1];
if (nearx < 0 || nearx >= grid.size() || neary < 0 || neary >= grid[0].size()) count++;
else if (grid[nearx][neary] == 0) {
// cout << nearx << ' ' << neary << endl;
count++;
}
}
}
int main() {
int N, M;
cin >> N >> M;
vector<vector<int>> grid(N, vector<int>(M, 0));
// 图的存储
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
cin >> grid[i][j];
}
}
for (int i = 0; i < N; i++) {
for (int j = 0; j < M; j++) {
if (grid[i][j] == 1) {
calPerimeter(grid, i, j);
}
}
}
cout << count << endl;
}
卡玛网110
题目描述:卡玛网110
文档讲解:代码随想录(programmercarl)110. 字符串接龙
梳理
-
首先需要对字符串进行存储。这里每一个字符串直接用cin即可
因为本题要求strList里的每个字符串只用使用一次,所以还需要定义一个unordered_set
类型的strSet表示其中的字符串是否被访问过 -
本题中使用广搜,对字符串进行搜索,在此过程中进行的操作是不断对字符串的某一位进行替换,而不是像之前岛屿问题那样计算相邻的陆地然后进行标记。最后就是要看结果是否等于endStr。
这里替换的操纵就是用两个for循环,i遍历字符串的长度,j遍历26个字母,
newWord[i] = j + 'a' -
至于搜索的路径是不是最短路径,这里有说法
在无权图中,用广搜求最短路最为合适,广搜只要搜到了终点,那么一定是最短的路径
因为广搜就是以起点中心向四周扩散的搜索。
- 所以搜索方式就需要使用广搜来进行,同时因为最后输出的结果是一个路径的长度,需要在搜索的过程中不断记录当前现有路径的长度。这里就需要用到一个
unordered_map<pair<string, int>>来记录每一个字符串的路径长度值
卡玛网测试
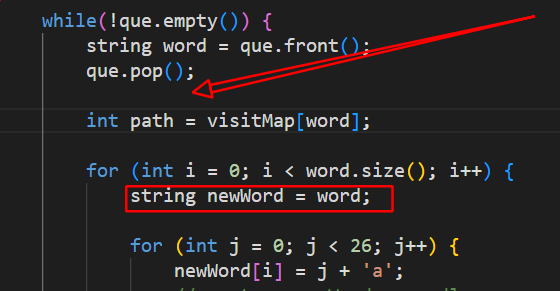
这个题有一个小细节需要注意,一直报错找了好久。我刚开始把newWord放在了箭头所指的位置,代码是下面的部分,就是会导致一个很隐蔽的问题,就是一旦在箭头所指的位置定义了newWord,那么他就无法保证每次只修改一位字符了。可能会修改很多位

如果放在正常的位置每次是只会修改一位,就不会改了前面的,还把后面的也改了。

while(!que.empty()) {
string word = que.front();
que.pop();
int path = visitMap[word];
for (int i = 0; i < newWord.size(); i++) {
string newWord = word;
for (int j = 0; j < 26; j++) {
点击查看代码
#include<iostream>
#include<vector>
#include<queue>
#include<unordered_map>
#include<unordered_set>
using namespace std;
int main() {
int N;
string str;
string startStr, endStr;
cin >> N;
cin >> startStr >> endStr;
unordered_set<string> strSet;
for (int i = 0; i < N; i++) {
cin >> str;
strSet.insert(str);
}
queue<string> que;
que.push(startStr);
unordered_map<string, int> visitMap;
visitMap.insert(pair<string, int>(startStr, 1));
while(!que.empty()) {
string word = que.front();
que.pop();
int path = visitMap[word];
for (int i = 0; i < word.size(); i++) {
string newWord = word;
// cout << newWord << endl;
for (int j = 0; j < 26; j++) {
newWord[i] = j + 'a';
if (newWord == endStr) {
cout << path + 1 << endl;
return 0;
}
else {
if (strSet.count(newWord) == 1 && visitMap.count(newWord) == 0) {
visitMap.insert(pair<string, int>(newWord, path + 1));
que.push(newWord);
}
}
}
}
}
cout << 0 << endl;
}
卡玛网105
题目描述:卡码网105
文档讲解:代码随想录(programmercarl)105.有向图的完全可达性
本题需要使用到邻接表的存储,核心就是用深搜或者广搜遍历一个有向图。在dfs中,k哥强调的地方是分两种情况,讨论处理当前结点和处理下一个结点
梳理
-
首先使用邻接表存储一个图。邻接表的使用需要用到vector<list
>这种类型,我们定义一个 vector<list<int>> graph(N + 1); -
之后使用深度优先遍历,对第一个结点指向的结点进行逐个遍历,处理的部分就是将其的visited数组标记为1即可。
需要注意的是,使用邻接表存储的图在dfs的参数有变化,分别是
void dfs(vector<list<int>> graph, int key, vector<int> &visited) -
如果最后visited数组所有的值的标记都是1了,那么就说明第一个结点可达所有的结点。
卡玛网测试
本题需要注意的一点就是,因为结点是从1开始记录的,那么申请一个数组的时候,就需要开辟(N + 1)的空间。举个例子,我们要存储[1, 2, 3, 4],那么开辟大小为5的数组,同时为了保证只存储4个,从i = 1开始遍历即可,如下。
for (int i = 1; i < visited.size(); i++) {
if (visited[i] == 0) {
cout << -1 << endl;
return 0;
}
}
剩下的代码思路比较好理解
处理当前结点
点击查看代码
#include<iostream>
#include<vector>
#include<list>
using namespace std;
void dfs(vector<list<int>> graph, int key, vector<int> &visited) {
if (visited[key] == 1) return;
visited[key] = 1;
list<int> keys = graph[key];
for (int key : keys) {
dfs(graph, key, visited);
}
}
int main() {
int N, K;
int s, t;
cin >> N >> K;
vector<list<int>> graph(N + 1);
// 图的存储
for (int i = 0; i < K; i++) { // 表示存储几条边,下标从0或者1开始都无所谓
cin >> s >> t;
graph[s].push_back(t);
}
vector<int> visited(N + 1, 0);
dfs(graph, 1, visited);
for (int i = 1; i < visited.size(); i++) {
if (visited[i] == 0) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
处理下一个结点
这个和之前99岛屿数量两个版本的深搜是一致的。
点击查看代码
#include<iostream>
#include<vector>
#include<list>
using namespace std;
void dfs(vector<list<int>> graph, int key, vector<int> &visited) {
list<int> keys = graph[key];
for (int key : keys) {
if (visited[key] == 0) {
visited[key] = 1;
dfs(graph, key, visited);
}
}
}
int main() {
int N, K;
int s, t;
cin >> N >> K;
vector<list<int>> graph(N + 1);
// 图的存储
for (int i = 0; i < K; i++) { // 表示存储几条边,下标从0或者1开始都无所谓
cin >> s >> t;
graph[s].push_back(t);
}
vector<int> visited(N + 1, 0);
visited[1] = 1;
dfs(graph, 1, visited);
for (int i = 1; i < visited.size(); i++) {
if (visited[i] == 0) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号