代码随想录算法训练营第43天|图论理论基础、深度优先搜索理论基础、98. 所有可达路径、广度优先搜索理论基础

图论理论基础

2025-03-18 18:14:29 星期二

视频讲解：如果学不会图论，是因为你没掌握基础！图论算法基础篇来咯！

代码随想录视频内容简记

1. 图的种类，无向图，有向图

2. 度，入度和出度。其中度是无向图的概念，入度和出度都是有向图的概念

3. 图的连通性

   1. 连通图。这是无向图中的概念

   2. 强连通图。这是有向图中的概念

   3. 连通分量。指的是极大连通子图，必须是极大，所以是无向图中的概念

   4. 强连通分量。指的是极大强连通子图，是有向图中的概念

4. 图的存储

   1. 朴素存储。就是创建一个\(n\times 2\)的矩阵，来表示每个点之间的连接情况
   
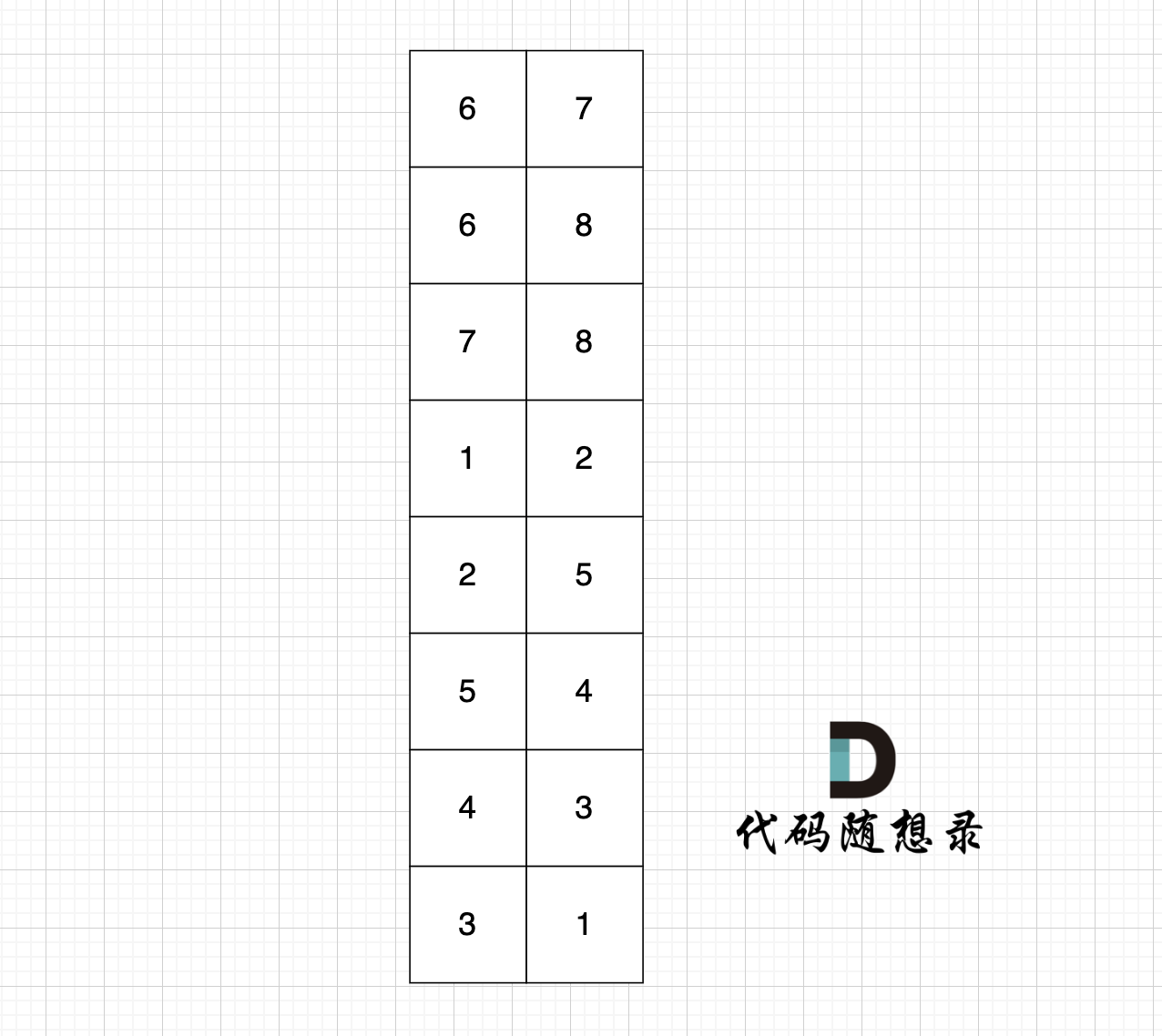
   2. 邻接矩阵。创建一个\(n\times n\)的二维矩阵。适合用来存储边多，点少的图。
   
   3. 邻接表。一个n的数组+链表。适合用来存储边少，点多的图
   

5. 图的遍历，分为深度优先搜索（DFS）和广度优先搜索（BFS），分别对应二叉树遍历的递归遍历和层序遍历

深度优先搜索理论基础

视频讲解：妈妈再也不在担心我的图论！！深度优先搜索理论基础来咯！ 深搜理论基础篇

代码随想录视频内容简记

深度优先搜索的模板

vector<vector<int>> result();
vector<int> path;
void dfs(参数) {
	if (终止条件) {
		存放结果;
		return;
	}
	for (选择：本结点连接的其他结点) {
		处理结点；
		dfs(图：选择的结点)；
		回溯操作；
	}
}

深搜三部曲

1. 确定递归函数和参数

2. 确定函数的终止条件

3. 处理目前结点出发的路径

卡玛网98

题目描述：卡玛网98
文档讲解：代码随想录(programmercarl)98. 所有可达路径
视频讲解：图论，深度优先搜索基础题，深搜详解 | 卡码网：98. 所有可达路径

代码随想录视频内容简记

梳理

1. 先对图进行存储

2. 深搜三部曲

   1. 确定递归函数和参数

   2. 确定终止条件

   3. 处理当前结点出发的路径

3. 打印输出

大致代码内容

1. 这里使用邻接矩阵进行存储。首先定义一个graph[n + 1][n + 1]，之后for (int i = 0; i < 边数；i++)，在循环内部对每一组连接的点进行赋值为1

2. 深搜三部曲

   1. void dfs (graph, x, n)，其中x表示当前结点，n表示终止结点

   2. if (x == n) {result.push_back(path); return;}

   3. for (int i = 1; i <= n; i++) ，这里i从1开始遍历，表示输入的结点是从1开始的，到5，而不是从0。之后if (graph[x][i] == 1) path.push_back(i);如果x和i之间有连接的话，那么将i添加到路径中，之后进入递归dfs(graph, i, n);，表示从i开始进行搜索。最后回溯，表示撤销，path.pop_back();

3. 打印输出，这里注意就是先要把第一个1存入到path中，才能进行遍历，否则后面所有的路径就没有1了。之后在打印输出的时候注意最后一个数字的后面没有空格。

卡玛网测试

有几点需要注意的就是，在深搜三部曲第三步，对于本题中，一定是需要在if (graph[x][i] == 1)的条件下，也就是当前结点之间确实有边进行连接的基础上才能进行

另外就是在进入递归之后，也就是dfs(graph, i, n)而不是dfs(graph, i + 1, n)，从当前连接的下一个结点开始搜索即可

点击查看代码

#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result;
vector<int> path;

// DFS深搜三部曲
void dfs(vector<vector<int>> graph, int x, int n) {
  if (x == n) {
    result.push_back(path);
    return;
  }
    
  for (int i = 1; i <= n; i++) {
    if (graph[x][i] == 1) {
      path.push_back(i);
      dfs(graph, i, n);
      path.pop_back();
    }
  }
}

int main() {
  int N, M;
  cin >> N >> M;
  int s, t;
  // 图的存储
  vector<vector<int>> graph(N + 1, vector<int>(N + 1, 0));
  for (int i = 0; i < M; i++) {
    cin >> s >> t;
    graph[s][t] = 1;
  }

  path.push_back(1);
  dfs(graph, 1, N);
  // 打印输出
  if (result.size() == 0) cout << -1 << endl;
  for (const vector<int> &pa : result) {
    for (int i = 0; i < pa.size() - 1; i++) {
      cout << pa[i] << " ";
    }
    cout << pa[pa.size() - 1] << endl;
  }
}

广度优先搜索理论基础

视频讲解：图论：广度优先搜索理论基础！ | 广搜理论基础

代码随想录视频内容简记

要点

广搜就是一圈一圈地进行搜索，先对中间的结点进行访问，之后对中间结点的上下左右进行访问

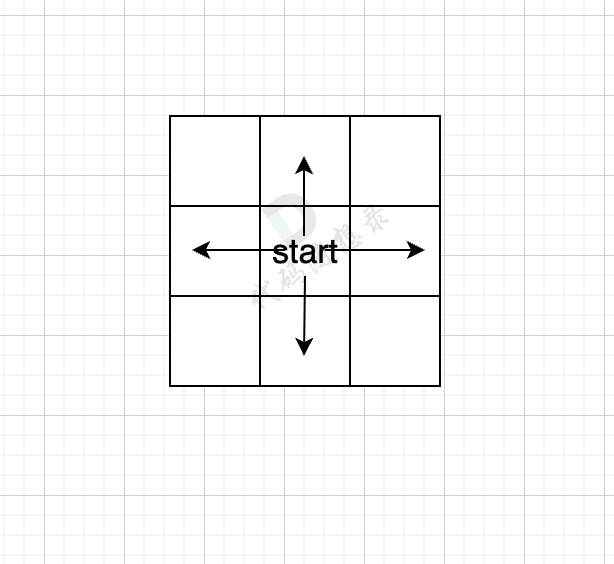
在广搜中一般需要用到队列来对访问元素进行添加，同时，需要引入一个visited数组对已经访问过的元素进行标记

梳理

1. 首先需要定义一个方向数组，来表示对当前结点的上下左右方向的元素进行访问

2. 定义bfs函数和参数

3. 广搜不是递归遍历的方式，适合队列紧密相关的，会将全部的结点都往队列中添加一遍

4. 注意要对越界访问和visited数组进行审查

代码框架

dir[4][2] = {0, 1, 1, 0, 0, -1, -1, 0};
void bfs(vector<vector<int>> grid, vector<vector<int>> visited, int x, int y) {
	queue<pair<int, int>> que;
	queue.push({x, y});
	visited[x][y] = 1; // 将起始结点进行标记
	// 开始遍历队列内元素
	while (!que.empty()) {
		cur = que.front();
		que.pop();
		for (int i = 0; i < 4; i++) {
			nextx = cur.first + dir[i][0];
			nexty = cur.second + dir[i][1];
			// 越界检查
			if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid.size()) continue;
			// visited数组检查
			if (visited[nextx][nexty] == 0) {
				// 将元素添加到队列中
				que.push({nextx, nexty});
				visited[nextx, nexty] = 1;
			}
		}
	}
}