代码随想录算法训练营第39天|115.不同的子序列、583. 两个字符串的删除操作、72. 编辑距离

LeetCode115

2025-03-14 15:28:10 星期五

题目描述：力扣115
文档讲解：代码随想录(programmercarl)115.不同的子序列
视频讲解：《代码随想录》算法视频公开课：动态规划之子序列，为了编辑距离做铺垫 | LeetCode：115.不同的子序列

代码随想录视频内容简记

本题就是在392的基础之上，做了一些修改，改为了判断有多少个子序列，而不是单纯判断是不是的问题了

梳理

1. 确定dp[i][j]数组的含义，表示在以i - 1为结尾的s中有以j - 1为结尾的个数为dp[i][j]

2. 确定递推公式，

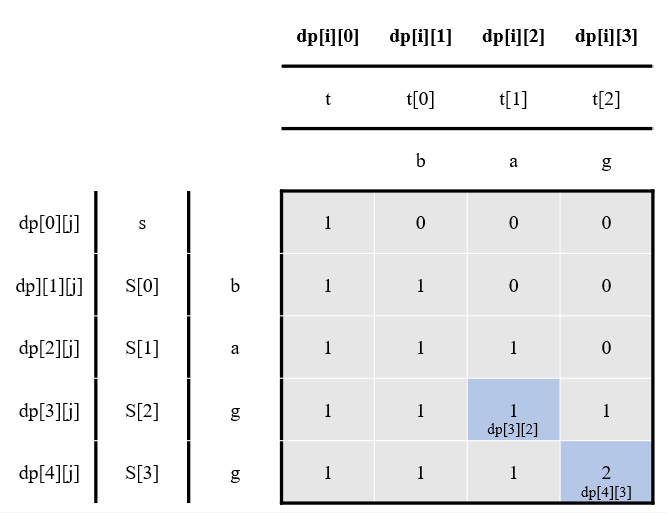
首先s[3]和t[2]相同，这里大致需要分成两种情况，一种就是使用s[i - 1]，另外一种就是不使用s[i - 1]

因为s[3]和t[2]相同，就说明肯定当前的"bagg"和"bag"是一对了，那么就是使用s[i - 1]。这里递推的时候就直接用dp[4 - 1][3 - 1]即可，代表以"bagg"结尾的s中有以"bag"结尾的t的个数；但是还有一种不使用s[i - 1]，那就回到s[i - 2]，图中的s[2]和t[2]，递推的时候就是使用dp[4 - 1]和[3]，代表以"bag"结尾的s中有以"bag"结尾的t的个数

3. 初始化dp数组，这个初始化首先是dp[i][0]，也就是最左边一列，都初始化为1(dp[0][0]也是1)，表示s删减到空了以后，t就是s的子序列。dp[0][j]就是最上面一行直接初始化为0即可，s是空串，那么t就没法做他的子序列。

4. 确定遍历顺序，从上到下，从左到右

5. 打印dp数组

LeetCode测试

这是第五道困难了把

点击查看代码

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));
        for (int i = 0; i < s.size(); i++) dp[i][0] = 1;
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                else dp[i][j] = dp[i - 1][j];
            }
        }
        return dp[s.size()][t.size()];
    }
};

LeetCode583

题目描述：力扣583
文档讲解：代码随想录(programmercarl)583. 两个字符串的删除操作
视频讲解：《代码随想录》算法视频公开课：LeetCode：583.两个字符串的删除操作

代码随想录视频内容简记

1. 确定dp[i][j]数组的含义，表示以i - 1结尾的word1和以j - 1结尾的word2进行删减操作到相同需要的最小操作次数为dp[i][j]

2. 确定递推公式

   1. 首先是如果word1[i - 1] == word2[j - 1]，表示两个字符相等，那么此时一个相同给的字符对两个单词来说没有任何影响，dp[i][j] = dp[i - 1][j - 1]

   2. 但是如果word1[i - 1] != word2[j - 1]，那么需要分几种情况，首先是只对word1进行操作，比如"ac"和"a"那么就是dp[i - 1][j] + 1;然后是只对word2进行删减，那么就是dp[i][j - 1] + 1;再然后就是对两个单词都进行删减，比如"ac"和"ae"，就需要dp[i - 1][j - 1] + 2;

   3. 最后要对这三种情况进行取min，也就是min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2)，因为是最小操作次数

3. 初始化dp数组，dp[i][0]这一列，需要初始化为i，dp[0][j]这一列需要初始化为j

4. 确定遍历顺序，从左往右，从上到下

5. 打印dp数组

LeetCode测试

这个题在初始化的时候记得取等于号。

点击查看代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 2);
            }
        }
        return dp[word1.size()][word2.size()];
    }

};

LeetCode72

题目描述：力扣72
文档讲解：代码随想录(programmercarl)72. 编辑距离
视频讲解：《代码随想录》算法视频公开课：动态规划终极绝杀！ LeetCode：72.编辑距离

代码随想录视频内容简记

本体和上一道两个字符串的删除操作非常类似，在编辑距离中，有增，删和替换，其中增的删的两种操作都是可以的，就是互相可以替换的，比如s="ab"和t="a"，那么删除掉s中的b和增加t中的b带来的效果都是一样的。

1. 确定dp[i][j]的含义，表示以i - 1结尾的word1和以j - 1结尾的word2的最小操作次数为dp[i][j]

2. 确定递推公式，首先是两个元素相同的情况，就是word1[i - 1] == word2[j - 1]，那么就是dp[i][j] = dp[i - 1][j - 1]，这样对两个单词来说就不用操作了，直接由前面的单词部分继承过来即可，和583两个字符串的删除是一样的

   接着是两个元素不同的情况，分为了增，删，和替换。因为增和删对操作次数的变化都是一样的，所以只需要列出删除时dp的变化即可

   删除：只删除word1或者word2即可
   dp[i][j] = dp[i - 1][j] + 1;

   dp[i][j] = dp[i][j - 1] + 1;

   替换：需要对一个元素进行替换操作
   dp[i][j] = dp[i - 1][j - 1] + 1;

   比如：对"ab"和"ac"来说，我们要得到的是dp[2][2]，比较的是word1[1]和word2[1]，也就是"b"和"c"，那么只需要回到dp[1][1]的状态，也就是"a"和"a"的情况，之后再进行加1就可以得到此时的状态了。

   (那明明只是删除了一个元素，为什么需要两个都是[i - 1]，[j - 1]呢？可以理解为，此时一旦两个元素不等了，那么只需要替换任意一个即可，至于i - 1和j - 1只是为了继承于上一个状态，在这个基础上加1）

   最后取min即可

3. 初始化dp数组，dp[i][0]需要初始化为i，dp[0][j]需要初始化为j，和上一道题一样

4. 确定遍历顺序，从左往右遍历，从上往下遍历即可

5. 打印dp数组

LeetCode测试

点击查看代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); j++) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); i++) {
            for (int j = 1; j <= word2.size(); j++) {
                if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
                else {
                    dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + 1);
                }
            }
        }
        return dp[word1.size()][word2.size()];
    }
};