代码随想录算法训练营第38天|1143.最长公共子序列、1035.不相交的线、53. 最大子数组和、392.判断子序列

LeetCode1143

2025-03-12 18:51:29 星期三<<<<<今天老开心了哈哈😀😁😃😄，hamburger🍔day

题目描述：力扣1143
文档讲解：代码随想录(programmercarl)1143.最长公共子序列
视频讲解：《代码随想录》算法视频公开课：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列

代码随想录视频内容简记

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

梳理

1. 确定dp[i][j]数组的含义，表示以(0, i - 1)结尾的nums1和以(0, j - 1)结尾的nums2结尾的最长公共子序列的长度为dp[i][j]

2. 确定递推公式，首先是从i - 1和j - 1推导过来的，这个用if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i-- 1][j - 1] + 1

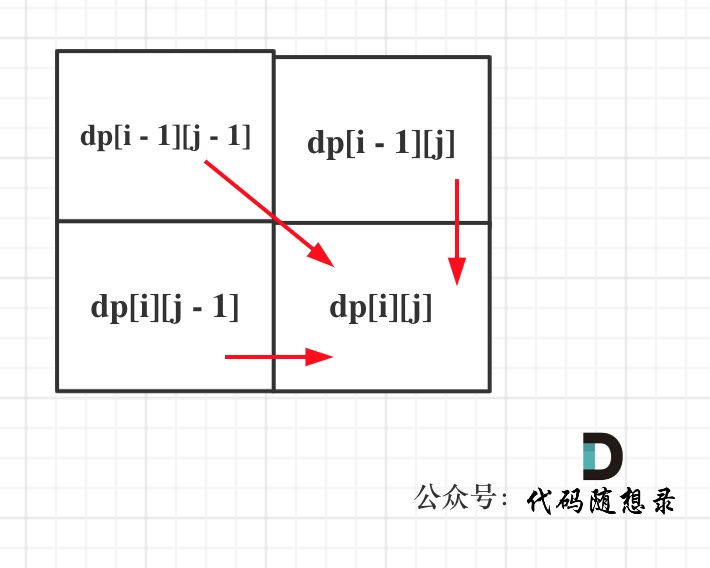
然后是从dp[i - 1][j]和dp[i][j - 1]推导过来的，这个是和上一道最长公共子数组不一样的地方，用else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

举个例子，如果是"abc"和"ace"两个字符串，c和e不匹配了，那么此时"abc","ace"两个字符串的最长公共子序列长度就可以转换为"ab","ace"的和"abc","ac"的最长公共子序列长度，不要加1此时

3. 初始化dp数组，这个用i - 1，j - 1表示的话就没有疑问，直接最左一列和最上一行初始化为0，也就是整个数组初始化为0即可

4. 确定遍历顺序，直接从左到右，从上到下即可

5. 打印dp数组

LeetCode测试

点击查看代码

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));
        for (int i = 1; i <= text1.size(); i++) {
            for (int j = 1; j <= text2.size(); j++) {
                if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
            }
        }
        return dp[text1.size()][text2.size()];
    }
};

LeetCode1035

题目描述：力扣1035
文档讲解：代码随想录(programmercarl)1035. 不相交的线
视频讲解：《代码随想录》算法视频公开课：动态规划之子序列问题，换汤不换药 | LeetCode：1035.不相交的线

代码随想录视频内容简记

本题说返回不相交的直线的最大数量，其实就是判断两个数组的最长公共子序列的长度即可，示例给的是nums1 = [1,4,2], nums2 = [1,2,4]，那么公共子序列就是[1,4,2]和[1,4]

LeetCode测试

只能说一摸一样

点击查看代码

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
        for (int i = 1; i <= nums1.size(); i++) {
            for (int j = 1; j <= nums2.size(); j++) {
                if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

LeetCode53

题目描述：力扣53
文档讲解：代码随想录(programmercarl)53. 最大子数组和
视频讲解：《代码随想录》算法视频公开课：看起来复杂，其实是简单动态规划 | LeetCode：53.最大子序和

代码随想录视频内容简记

子数组是数组中的一个连续部分。

这个题之前的贪心思路的解法在这里，核心就是前面的子数组如果加上nums[i]变成了负数，那么nums[i]没有用，直接跳过重新开始子数组和的累加

这道题如果用动归的思路，本题用一个一维的dp数组就可以

1. 确定dp数组的含义，表示以nums[i]为结尾的最大子数组的和

2. 确定递推公式，就是确定dp[i]如何进行推出，就是分两种情况。这个就需要搞明白，一个子数组(其实也就是子序列)，他的本身nums[i]也是整个数组的一个子数组，就比如，[1,4,5]的子数组不仅有前面的[1,4]，还有本身的[5,]。

   对于dp来说，表示的子数组的和，所以也包括两个部分，一个是前面的dp[i - 1]，另外一个就是nums[i]本身。所以dp[i] = max(dp[i - 1] + nums[i], nums[i])

3. 初始化dp数组，dp[0] = nums[0]，剩下的非零下标也都初始化为0即可

4. 确定遍历顺序，从小到大即可

5. 打印dp数组

LeetCode测试

本题有几个小细节需要注意

1. 在初始化result的时候，需要注意，不能初始化为0，也不能初始化为INT_MIN，必须初始化为nums[0]，这里有个测试用例，就是[-1,-2]，正常输出应该是-1，但是但是因为递推是从1开始的，所以直接跳过了dp[0]，此时dp[0]如果比后面的大就错了

2. 另外就是一个[1]的话不进入递推，直接返回nums[0]即可

点击查看代码

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int> dp(nums.size() + 1, 0);
        if (nums.size() == 1) return nums[0];
        dp[0] = nums[0];
        int result = nums[0];
        for (int i = 1; i < nums.size(); i++) {
            dp[i] = max(dp[i - 1] + nums[i], nums[i]);
            result = max(result, dp[i]);
        }
        return result;
    }
};

LeetCode392

题目描述：力扣392
文档讲解：代码随想录(programmercarl)392.判断子序列
视频讲解：《代码随想录》算法视频公开课：动态规划，用相似思路解决复杂问题 | LeetCode：392.判断子序列

代码随想录视频内容简记

本题和1143最长公共子序列其实是非常相似的，就是只要判断s和t的最长公共子序列的长度等于s的长度，那么就可以说明s是t的子序列。区别在哪里呢？就是递推公式不同

1. 确定dp[i][j]数组的含义，表示以i为结尾的s和以j为结尾的t的最长共工子序列的长度为dp[i][j]

2. 确定递推公式，这里就是单纯要判断s是不是t的子序列，那么只需要在t中做元素的删减即可。可以看到，这里的递推是只有两个方向的，一个是左上，一个是左边

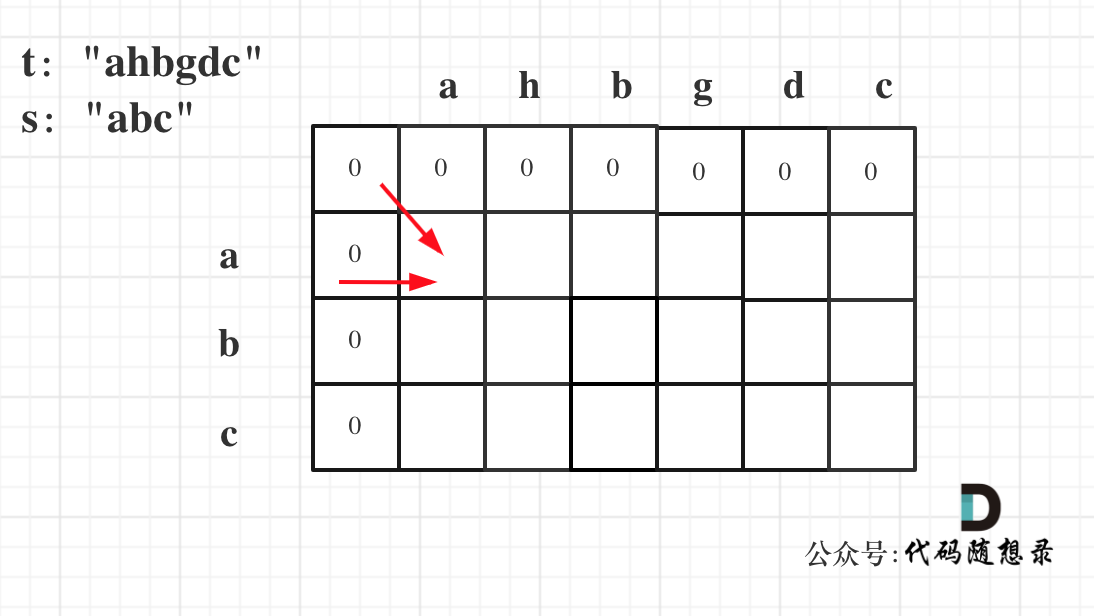
注意上图就是左边的是s，上面的是t，这个也是分两个部分，和上面的都一样

首先是连续的情况，那么递推公式就是，if (nums[i - 1] == nums[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1

然后是不连续需要进行删减，那么就是 else dp[i][j] = dp[i][j - 1]，就是行不变，列发生变化

3. 初始化dp数组，和1143都一样，全部初始化为0即可

4. 确定遍历顺序，从左到右，从上到下

5. 打印dp数组

LeetCode测试

点击查看代码

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>> dp(s.size() + 1, vector<int> (t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = dp[i][j - 1];
            }
        }
        if (dp[s.size()][t.size()] == s.size()) return true;
        return false;
    }
};