代码随想录算法训练营第37天|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
LeetCode300
2025-03-10 19:46:18 星期一
题目描述:力扣300
文档讲解:代码随想录(programmercarl)300.最长递增子序列
视频讲解:《代码随想录》算法视频公开课:动态规划之子序列问题,元素不连续!| LeetCode:300.最长递增子序列
代码随想录视频内容简记
梳理
-
确定dp数组的含义,dp[i]表示以nums[i]结尾的最长递增子序列的长度为dp[i]
-
确定递推公式,
if (nums[j] < num) dp[i] = max(dp[j] + 1, dp[i]);,这里解释一下,就是因为dp[i]是不断在dp[j]的基础上进行子序列的长度递增的,但是又因为在i的遍历过程中,dp[i]之前的dp[i - 1],dp[i - 2]...都要求出来,但是到dp[i]不一定是最大的,所以要到nums[i]结尾的最长递增子序列必须要进行max取值 -
初始化dp数组,
dp[0] = 1即可,表示下标为0的nums[0]的最长递增子序列就是本身,所以是1 -
确定遍历顺序,i从小到打大遍历即可。因为这个dp数组求出来的是每一个元素的最长递增子序列,所以在最后需要遍历一遍把所有的dp求max
-
打印dp数组
LeetCode测试
本题注意,每一个dp[i]的大小都最少为1,所以在定义dp数组的时候不能初始化为0了,需要都初始化为1
点击查看代码
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> dp(nums.size(), 1);
dp[0] = 1;
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) dp[i] = max(dp[j] + 1, dp[i]);
}
}
int result = 0;
for (int i = 0; i < nums.size(); i++) {
result = max(dp[i], result);
}
return result;
}
};
LeetCode674
题目描述:力扣674
文档讲解:代码随想录(programmercarl)674. 最长连续递增序列
视频讲解:《代码随想录》算法视频公开课:动态规划之子序列问题,重点在于连续!| LeetCode:674.最长连续递增序列
LeetCode测试
这个题在上道的基础上稍改一下递推公式就行,很简单
点击查看代码
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
vector<int> dp(nums.size(), 1);
dp[0] = 1;
for (int i = 1; i < nums.size(); i++) {
if(nums[i - 1] < nums[i]) dp[i] = max(dp[i - 1] + 1, dp[i]);
}
int result = 0;
for (int i = 0; i < nums.size(); i++) {
result = max(dp[i], result);
}
return result;
}
};
LeetCode718
题目描述:力扣718
文档讲解:代码随想录(programmercarl)718. 最长重复子数组
视频讲解:《代码随想录》算法视频公开课:动态规划之子序列问题,想清楚DP数组的定义 | LeetCode:718.最长重复子数组
代码随想录视频内容简记
-
确定dp数组的含义,dp[i][j]表示num1中以i - 1为结尾的数组和num2中以j - 1为结尾的数组的最长的最长重复子数组长度为dp[i][j]。
关于这里为什么要定义以i - 1结尾和以j - 1为结尾?这是为了方便进行初始化,因为,当i = 0和j = 0时,
dp[-1][j]这一行和dp[i][-1]这一列的表示是非法的,所以将最左列和最上行初始化为0,那么就可以直接从下标为1开始遍历,就都是合法的了。如果定义以i和j结尾的话,那么i = 0,j = 0时,初始化的dp[0][j]这一行和dp[i][0]这一列的表示就合法了,那么初始化的部分就需要多加for循环来进行,而递推使用的dp[i - 1][j - 1],还会有-1的情况出现,所以就还要要求有和合法性判断,比较麻烦。
以i - 1和j - 1为表示的
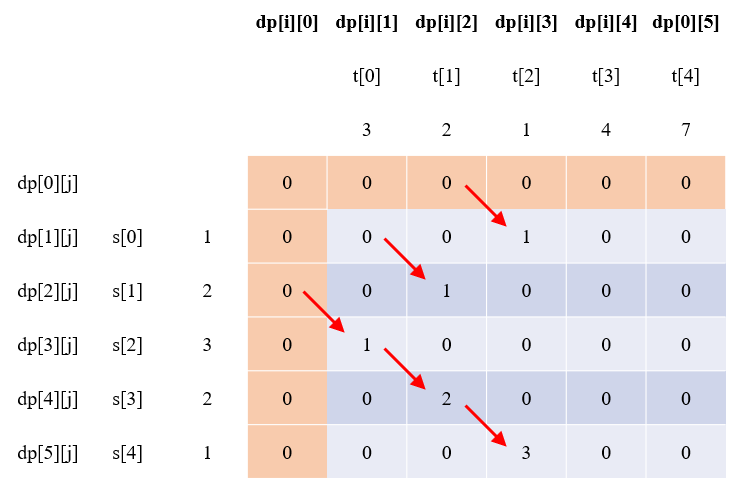
以i和j为表示的
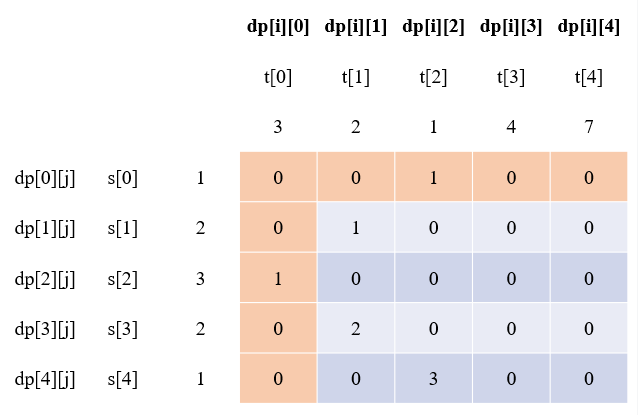
能看出来二者的dp数组是不一样的
-
确定递推公式,这里用i - 1和j - 1的方式。
if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1 -
初始化dp数组,第一行和第一列都需要初始化为0,因为下面的推导需要这样来进行初始化,对于非零下标,也都初始化为0即可
-
确定遍历顺序,从小到大遍历即可
-
打印dp数组
LeetCode测试
以i-1和j-1为表示
-
注意,这里的打印数组在提交的时候不要加上打印的部分,会超时
-
在循环的时候,因为for循环直接定义的是下标-1,所以最后的条件判断语句也要改成<=
点击查看代码
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int result = 0;
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
result = max(dp[i][j], result);
}
// cout << dp[i][j] << ' ';
}
// cout << endl;
}
return result;
}
};
以i和j为表示
这种的有两个需要注意的点
-
首先是因为dp[0][0]的合法性,那么for循环的起始就要从0开始
-
这里需要注意的一个点就是
if (nums1[i] == nums2[j] && i > 0 && j > 0) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
result = max(dp[i][j], result);
这里的result不能写在if判断里,否则会漏掉一种情况,第55个测试用例是[1,2,3,2,8]
,[5,6,1,4,7]。打印出来的dp数组实际上是
0 0 1 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
根本没有加的操作,但是最小重复子数组应该是1没错,如果resule放在if里面,会自动漏掉初始的最上一行和最左一列,导致出错,而用i - 1和j - 1就不会出现这种情况,因为初始化都为0,所以result直接跟着递推公式走就行。
点击查看代码
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));
int result = 0;
for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;
for (int i = 0; i < nums1.size(); i++) {
for (int j = 0; j < nums2.size(); j++) {
if (nums1[i] == nums2[j] && i > 0 && j > 0) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
result = max(dp[i][j], result);
cout << dp[i][j] << ' ';
}
cout << endl;
}
return result;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号