代码随想录算法训练营第13天|222.完全二叉树的结点个数、110.平衡二叉树、257.二叉树的所有路径、404.左叶子之和
LeetCode222
题目描述:力扣222
文档讲解:代码随想录(programmercarl)222.完全二叉树的结点个数
视频讲解:《代码随想录》算法视频公开课:要理解普通二叉树和完全二叉树的区别! | LeetCode:222.完全二叉树节点的数量
代码随想录视频内容简记
普通二叉树解法
采用一般的后序遍历,依次对左右子树的节点个数进行统计,之后中间的数量是左右相加再+1,直接return即可
利用完全二叉树的性质来解
首先需要清楚完全二叉树
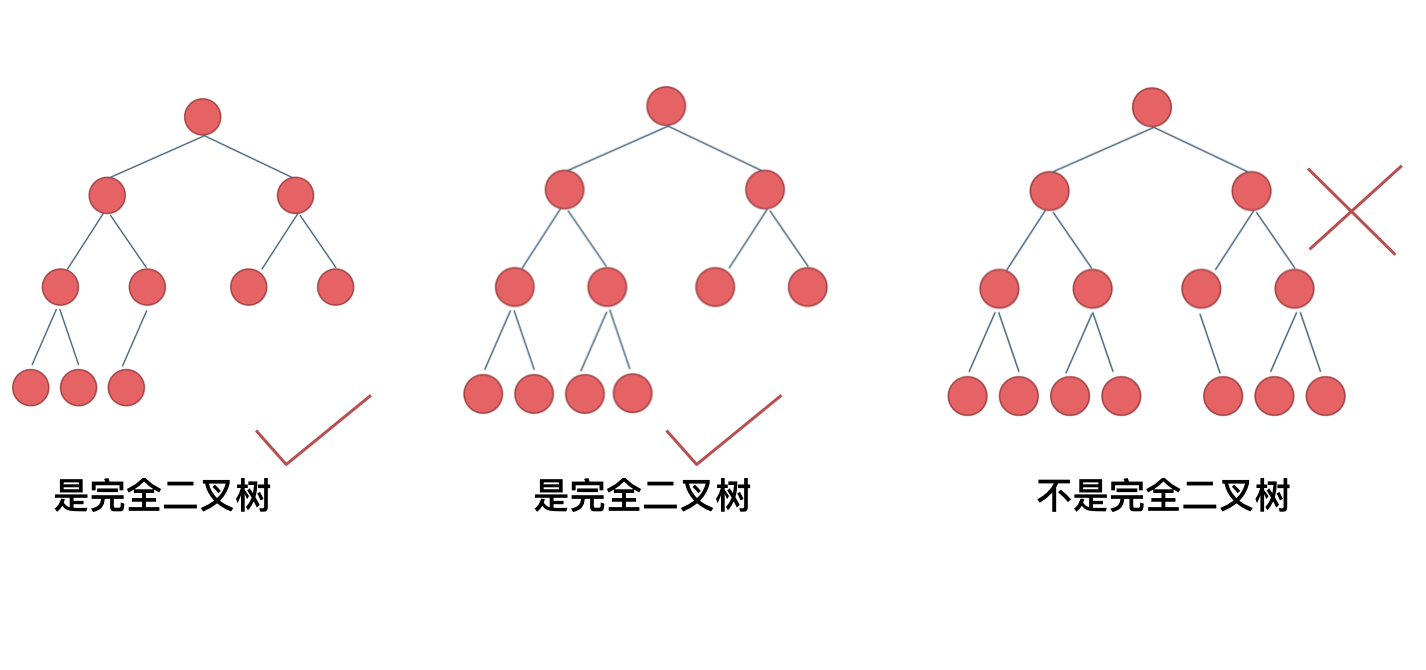
完全二叉树的性质就是可以将这棵树根节点开始的左子树和右子树不断遍历,直到找到他的左子树深度和右子树深度相等的情况。
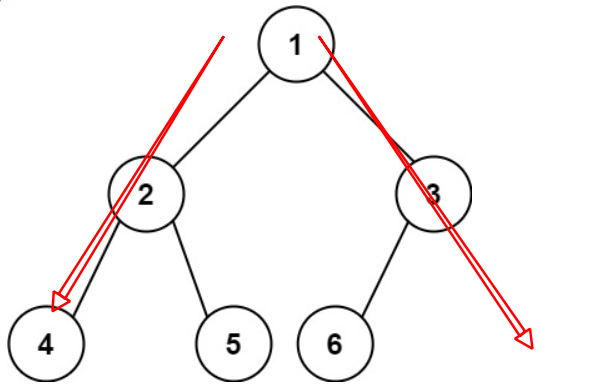
此时从这个根节点开始的树就是一棵满二叉树。而一颗满二叉树就可以用\(num = 2^{depth} - 1\)来计算
这种方法的特殊性就在于终止条件有两个,一个是结点为空,另一个就是左子树深度和右子树深度相等
梳理
-
确定函数的返回值和参数
-
确定递归的终止条件
-
确定单层递归的逻辑
大致代码内容
这种方法的流程就是从根结点的左右一直向下遍历,得到一棵棵满二叉树之后返回给上一层进行统计

-
if (root == NULL) return 0,这是第一个。另外就是不断向左和右分别遍历,分别定义一个ldepth和一个rdepth,之后用while (left)和while (right)分别遍历,对ldepth和rdepth进行++操作。if (ldepth == rdepth) return (2 << ldepth) - 1,这里用到了位运算,向左移动ldepth个位,表示\(2^{ldepth}\)。注意,这里的位运算必须加上括号,要不然会报错 -
单层递归就还是,
int lnum = countNode(root->left)。这里也要注意,如果在countNodes函数中直接传入root结点,那么就没法递归了。 -
最后返回中间处理的
result即可
LeetCode测试
点击查看代码
class Solution {
public:
int countNodes(TreeNode* root) {
if (root == NULL) return 0;
TreeNode* left = root->left;
TreeNode* right = root->right;
int ldepth = 0, rdepth = 0;
while (left) {
left = left->left;
ldepth++;
}
while (right) {
right = right->right;
rdepth++;
}
if (ldepth == rdepth) return (2 << ldepth) - 1;
int lnum = countNodes(root->left);
int rnum = countNodes(root->right);
int result = lnum + rnum + 1;
return result;
}
};
LeetCode110
题目描述:力扣110
文档讲解:代码随想录(programmercarl)110.平衡二叉树
视频讲解:《代码随想录》算法视频公开课:后序遍历求高度,高度判断是否平衡 | LeetCode:110.平衡二叉树
代码随想录视频内容简记
关于平衡二叉树的定义
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1
既然是求高度,依旧是采用后序遍历递归的方式
梳理
-
依旧是三部曲,确定函数的参数和返回值
-
确定递归的终止条件
-
确定单层递归的逻辑
大致代码内容
-
递归的出口还是
if (root == NULL) return 0 -
这里用如果左右子树的高度不相等就返回
-1的逻辑,首先定义两个int lheight = getHeight(root->left),之后if (lheight == -1) return -1。处理右子树的逻辑是一样的 -
最后处理中间,要对左右做差,
return abs(lheight - rheight) > 1 ? -1 : 1 + max(lheight, rheight)
这里的意思就是abs(lheight - rheight)的值如果大于1,那么就返回-1,如果小于等于1,那么就返回max(lheight, rheight) + 1,sam运算符一个?一个:其实质就是对两种情况做选择
- 注意这个题做的时候使用两个函数,一个是用bool返回最后的true或false,一个是int getHeight用来遍历求高度的,第一遍写的时候直接用bool去递归bool最后的结果是错的。用bool调用getHeight,getHeight自身递归
LeetCode测试
点击查看代码
class Solution {
public:
int getHeight(TreeNode* root) {
if (root == NULL) return 0;
int lheight = getHeight(root->left);
if (lheight == -1) return -1;
int rheight = getHeight(root->right);
if (rheight == -1) return -1;
return abs(lheight - rheight) > 1 ? -1 : 1 + max(lheight, rheight);
}
bool isBalanced(TreeNode* root) {
int result = getHeight(root);
return result == -1 ? false : true;
}
};
LeetCode257
题目描述:力扣257
文档讲解:代码随想录(programmercarl)257.二叉树的所有路径
视频讲解:《代码随想录》算法视频公开课::递归中带着回溯,你感受到了没?| LeetCode:257. 二叉树的所有路径
再一次看自己写的,自己都看不懂😅
代码随想录视频内容简记
这个题涉及到了递归和回溯,而且,因为要进行回溯,该题用的是前序遍历,至于说什么时候回溯?回溯的过程是和递归连在一起的,k哥说两个是不能分开的。具体到本题说,就是在递归的终止条件到达时,要进行上面几次递归累积起来这么些层的回溯操作,依次弹出。
感觉这个题很有必要去看下代码随想录的原文档,第一遍听讲有点绕不过来。
梳理
-
首先是要定义一个不带返回值的
traversal函数,里面要对字符串路径做引用,随时修改。其次还要有一个result数组存放path路径。注意这里的path是vector型的,方便进行回溯和添加处理 -
递归的终止条件,就是k哥说的不能简单的写
if (root == NULL) return。这里如果直接写root == NULL,就指到叶子结点的下面去了,如果直接if (root != NULL && root->left == NULL && root->right == NULL),那就才是叶子结点本身,所以k哥也说了root == NULL会比较麻烦
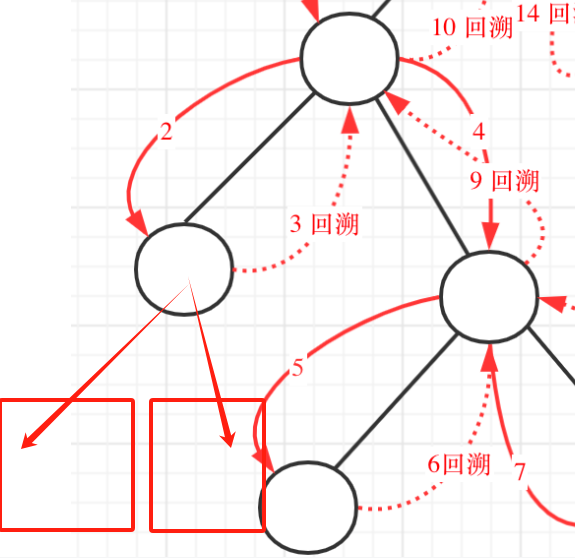
注:图片来自代码随想录
- 确定单层递归的逻辑,按照前序的中左右,但是为了让中能够在if终止条件返回之前在path最后加上最后一个结点,把中的位置做了调前
大致代码内容
-
确定递归的终止条件
if (cur->left == NULL && cur->right == NULL),有了这行代码可以对字符串的路径进行处理 -
分别是对中,前,后进行遍历
对中间结点的处理,这里path.push_back(root->val);是放在了终止条件之前,这里有其必然性,因为即使不进行叶子结点的判断,也要将其添加,所谓“燕过留痕”
left是这样,注意这里的回溯是对path进行的回溯,而不是result。这里就不多解释了,我现在脑子也乱了
if (left) {
traversal();
path.pop_back();
}
中是直接加入结点path.push_back(left->val)
- 还有一点就是这个题在力扣中是定义了一个
traversal()函数,供力扣给出的vector函数调用,注意如果根节点直接为空,那么就是直接返回空的result,if (root == NULL) return result
LeetCode测试
感觉这个题不好写的,有点头晕😵。
点击查看代码
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
path.push_back(cur->val);
if (cur->left == NULL && cur->right == NULL) {
string sPath;
for (int i = 0; i < path.size() - 1; i++) {
sPath += to_string(path[i]);
sPath += "->";
}
sPath += to_string(path[path.size() - 1]);
result.push_back(sPath);
return;
}
if (cur->left) {
traversal(cur->left, path, result);
path.pop_back();
}
if (cur->right) {
traversal(cur->right, path, result);
path.pop_back();
}
}
vector<string> binaryTreePaths(TreeNode* root) {
vector<int> path;
vector<string> result;
if (root == NULL) return result;
traversal(root, path, result);
return result;
}
};
LeetCode404
题目描述:力扣404
文档讲解:代码随想录(programmercarl)404.左叶子之和
视频讲解:《代码随想录》算法视频公开课::二叉树的题目中,总有一些规则让你找不到北 | LeetCode:404.左叶子之和
左叶子的定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
代码随想录视频内容简记
这道题目核心就是在递归的终止条件时,必须确定有“父与子”的关系,也就是必须保证叶子必须是左孩子
遍历的顺序还是采用的后序遍历
本题的递归遍历稍显特殊,因为用的是int型函数进行递归遍历,所以要注意一下这种写法。
梳理
-
确定函数的参数和返回值,本题直接给的
int函数,不再定义额外的函数 -
确定递归的终止条件,本题有两个
-
确定单层递归的逻辑,只需对左子树进行条件判断,右子树直接遍历
大致代码内容
-
定义一个
sumOfLeftLeaves()函数 -
第一个终止条件,确定该结点是遍历出的,
if (root == NULL) return 0。第二个终止条件,确定该结点是叶子结点,if (root->left == NULL && root->right == NULL) return 0 -
对左遍历的条件
if (root != NULL && root->left->left == NULL && root->left->right == NULL)
LeetCode测试
注意,在定义左叶子结点个数时,直接进入递归,之后在每一层的递归中用if判断是否进行相加操作
int lnum = sumOfLeftLeaves(root->left)直接用这个定义好,下面进行判断
点击查看代码
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 0;
// 向左遍历
int lnum = sumOfLeftLeaves(root->left);
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
lnum += root->left->val;
}
// 向右遍历
int rnum = sumOfLeftLeaves(root->right);
int num = 0;
num = lnum + rnum;
return num;
}
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号