集成学习

        集成学习(Ensemble learning)通过构建并结合多个机器学习模型来构建更强大模型的方法。集成学习的一般结构为：先产生一组“个体学习器”，

  再用某种策略将它们结合起来。集成中只包含同种类型的个体学习器，称为同质，当中的个体学习器亦称为“基学习器”，相应的算法称为“基学习

  算法”。集成中包含不同类型的个体学习器，称为“异质”，当中的个体学习器称为“组建学习器”。要获得好的集成，个体学习器应“好而不同”，即个

 体学习器要有一定的“准确性”，即学习器不能太坏，并且要有多样性，即个体学习器间具有差异。

  根据个体学习器的生成方式，目前的集成学习方法大致可以分为两类：Bagging和Boosting

 

 1. 结合策略

 

集成算法就是训练一堆基学习器，然后通过某种策略把各个基学习器的结果进行合成，从而得到集成学习器的结果。下面我们就来认识一下常用的结合策略：

(1)、平均法(Averaging)

   当基学习器输出的是连续数值，即$h_{i}(x)\epsilon \mathbb{R}$时，最常见的结合策略为平均法。

   (1)简单的平均法

     $H(x)=\frac{1}{k}\sum_{i=1}^{k}h_{i}(x)$

   (2)加权平均法(weighted averaging)

       $H(x)=\sum_{i=1}^{k}w_{i}h_{i}(x) $ ，其中$w_{i}$为权重系数，通常要求$w_{i}\geq 0，\sum_{i=1}^{k}w_{i}=1$。

       注：加权平均法的权重一般从训练数据中学习而得，对规模比较大额集成来说，要学习的权重比较多，较容易导致过拟合，因此加权平均法不一定

    优于简单平均法。 一般而言，在个体学习器性能相差较大时宜使用加权平均法，而在个体学习器性能相近时宜使用简单平均法。

(2)投票法(Voting)

      对分类来说，学习器$h_{i}(x)$将从类别集合中预测出一个类别标记，最常用的是投票法。

      (1)绝对多数投票法(majority voting)

         即如某标记的投票过半数，则预计为该标记；否则拒绝预测。

 

      (2)相对多数投票法(plurality voting)

           即预测为得票最多的标记，若同时出现多个票数最多，则任选其一。

 

      (3)加权投票法(weighted voting)

           $H(x)=\underset{j}{argmax}\sum_{i=1}^{k}w_{i}h_{i}^{j}(x)$

(3)学习法(stacking)

         Stacking方法是指训练一个模型用于组合其他各个模型。在stacking中我们把个体学习器称为初级学习器,在stacking中我们把个体学习器称为

        初级学习器。先从初始数据集训练出初级学习器，然后“生成”一个新的数据集用于训练次级学习器。生成的该新数据中，初级学习器的输出被

        当做样例输入特征，而初始样本的标记仍被当做样例标记。也就是说，假设初级学习器有m个，那么对于一个原始数据集中的样本(x; y)，

        通过这m个初级学习器有m个输出$\left \{ h_{1}(x), h_{2}(x), \cdots , h_{m}(x)\right \}$ 把$\left \{ {h_{1}(x), h_{2}(x), \cdots , h_{m}(x); y}\right \}$作为

        新数据的一个样本，所以一个初级学习器的输出作为新数据集中对应样本的一个特征，而其标记为原始数据中该样本的标记,算法流程如下：

 

                       

 

 

            在训练阶段，次级学习器(用来结合结果的学习器)的训练数据集是利用初级学习器来产生的，若直接用初级学习器的训练集来产生训练数据集，

      则很有可能会出现过拟合，也就 是过拟合风险较大；所以一般在使用Stacking时，采用交叉验证或留一法的方式，用训练初级学习器未使用的样本来产生

     次级学习器的训练样本。下面以k=5折交叉验证作为例子：

          

     

 

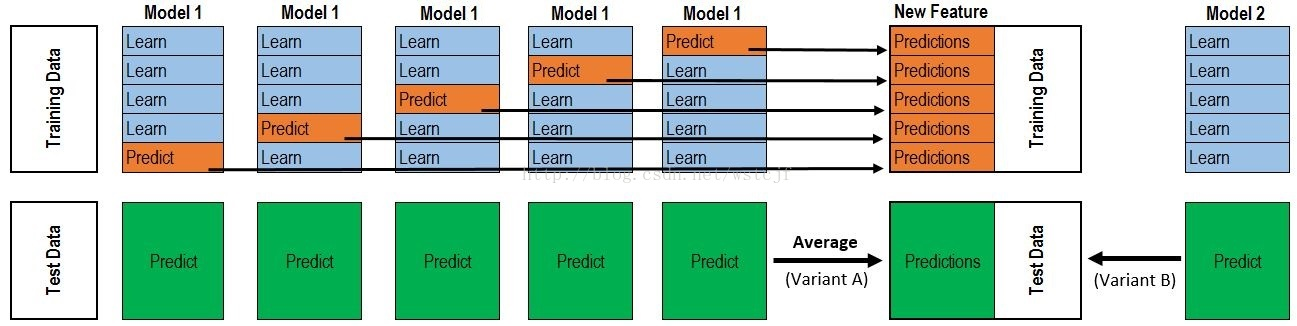
                   首先把整个数据集分成量训练集(Training Data)和测试集(Test Data)两部分，上图最左边，然后把训练数据集进行k折，此处k=5，

             即把训练数据分成5份， 在进行第j折时，使用其余的四份进行初级学习器的训练，得到一个初级学习器，并用该初始学习器把该折

            (即留下用来验证的)数据进行预测， 进行完所有折数，把预测输出作为新数据集的特征，即次级学习器的训练数据集，其中标记没变，

             用该新数据集训练次级学习器，从而得到一个完整的stacking。最后用原始数据的测试集来对该Stacking进行测试评估。次 级学习器

             的输入属性表示和次级学习算法的选择对Stacking集成的泛化性能有很大影响。

                  有研究表明，将初级学习器的输出类概率最为次级学习器的输入属性， 用多响应线性回归(Multi-reponse Linear Regression，简称MLR)作为

            次级学习器算法效果更好，在MLR中使用不同的属性集更佳。MLR是基于线性回归的分类器， 其对每个类分别进行线性回归，属于该类的训练样

           例所对应的输出为1，其他类置0，测试示例将被分给输出值最大的类。

 

2. Bagging

    Bagging算法 （Bootstrap aggregating），称为装袋算法。它是一种个体学习器之间不存在强依赖关系、可同时生成的并行式集成学习方法。

    bagging 基于自助采样法(bootstrap sampling)，也叫有放回重采样法，即给定包含m个样本的数据集，先随机从样本中取出一个样本放入采样

   集中,再把该样本返回初始数据集， 使得下次采样时该样本仍可以被选中，这样经过m次随机采样操作，就可以得到包含m个样本的采样集，

   初始数据集中有的样本多次出现，有的则未出现，其中，初始训练集中约有63.2%的样本出现在采样集中。

   照上面的方式进行 k 次操作，采样出 k 个含有m个训练集的采样集，然后基于每个采样集训练出 k个基学习器，再将这些基学习器进行结合，

   即可得到集成学习器。在对输出进行预测时，bagging通常对分类进行简单投票法，对回归使用简单平均法。

 

3.Boosting

    Boosting是一簇可将弱学习器提升为强学习器的算法。其工作机制为：先从初始训练集训练出一个基学习器，再根据基学习器的表现对样本分布

   进行调整，使得先前的基学习器做错的训练样本在后续收到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至

   基学习器数目达到实现指定的值T， 或整个集成结果达到退出条件，然后将这些学习器进行加权结合。