线性代数笔记02

蓝月の笔记——线性代数\(.02\)

视频链接

\(\mathfrak{Mathematics\ requires\ a\ small\ dose,\ not\ of\ genius,\ but\ of\ an\ imaginative\ freedom\ which,\ in\ a\ larger\ dose,\ would\ be\ insanity.}\)

数学需要的不是天赋，而是少量的自由想象，但想象太过自由又会陷入疯狂。

---

单位向量\((\text{Unit Vector})\)

单位向量也叫基向量\((\text{Basis Vector})\)，是坐标系中最基础的向量。下面是一些常见的单位向量。

\(\hat{\imath}\)

这是 \(x\) 轴方向上的单位向量，它代表 \(\begin{bmatrix}\ 1\ \\\ 0\ \\\end{bmatrix}\)。

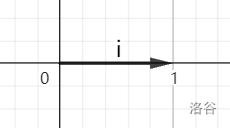
\(\hat{\jmath}\)

这是 \(y\) 轴方向上的单位向量，它代表 \(\begin{bmatrix}\ 0\ \\\ 1\ \\\end{bmatrix}\)。

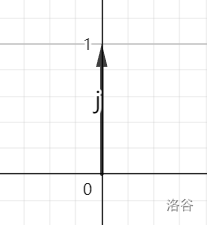
\(\hat{k}\)

\(\hat{k}\) 只有在三维向量上才存在。这是 \(z\) 方向上的单位向量。它代表 \(\begin{bmatrix}\ 0\ \\\ 0\ \\\ 1\ \\\end{bmatrix}\)。

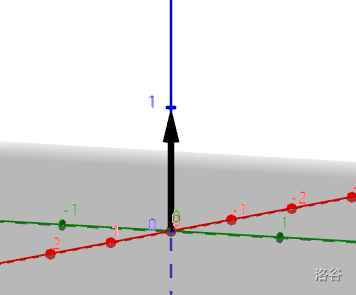
用途

如果我们把任意一个二维向量 \(\vec{v}=\begin{bmatrix}\ x\ \\\ y\ \\\end{bmatrix}\) 中的 \(x,y\) 看成标量，那么所有 \(\vec{v}\) 都可以由 \(\hat{\imath},\hat{\jmath}\) 缩放后相加得到。

例如：\(\begin{bmatrix}\ 3\ \\\ 2\ \\\end{bmatrix}=3\hat{\imath}+2\hat{\jmath},\begin{bmatrix}\ -3\ \\\ 1\ \\\end{bmatrix}=(-3)\hat{\imath}+1\hat{\jmath},\begin{bmatrix}\ 2\ \\\ -1\ \\\end{bmatrix}=2\hat{\imath}+(-1)\hat{\jmath}\)。

总结： \(\begin{bmatrix}\ x\ \\\ y\ \end{bmatrix}=x\hat{\imath}+y\hat{\jmath}\)。

三维向量同理： \(\begin{bmatrix}\ x\ \\\ y\ \\\ z\ \\\end{bmatrix}=x\hat{\imath}+y\hat{\jmath}+z\hat{k}\)。

线性组合\((\text{Linear Combination})\)

一个简短的基础概念。

如果 \(a,b\) 是标量且 \(a,b \in \mathbb{R}\)，那么我们称每一个 \(a\vec{v}+b\vec{w}\) 为 \(\vec{v}\) 和 \(\vec{w}\) 的线性组合。

张成的空间\((\text{Span})\)

给定两个向量 \(\vec{v}=\begin{bmatrix}\ x_1\ \\\ y_1\ \\\end{bmatrix},\vec{w}=\begin{bmatrix}\ x_2\ \\\ y_2\ \\\end{bmatrix}\)。

定义 \(\vec{v}\) 和 \(\vec{w}\) 张成的空间为：对于任意 \(a,b \in \mathbb{R}\)，每一个关于 \(\vec{v}\) 和 \(\vec{w}\) 的线性组合形成的空间。

例如 \(\vec{v}=\begin{bmatrix}\ 3\ \\\ 2\ \\\end{bmatrix},\vec{w}=\begin{bmatrix}\ 2\ \\\ -1\ \\\end{bmatrix}\)，那么 \(\vec{v}\) 和 \(\vec{w}\) 张成的空间就是整个二维平面，即整个平面直角坐标系。其中 \(a,b \in \mathbb{R}\)。

在大部分情况下，张成的空间时整个二维平面，但肯定有例外。

如果两个向量共线，那么它们张成的空间就是他们共的这条线。

例如：\(\vec{v}=\begin{bmatrix}\ 2\ \\\ 2\ \end{bmatrix},\vec{w}=\begin{bmatrix}\ 3\ \\\ 3\ \end{bmatrix}\)，他们张成的空间就是 \(y=x\) 这一条直线。

还有更特殊的情况，当两个向量都是零向量，即 \(\begin{bmatrix}\ 0\ \\\ 0\ \end{bmatrix}\) 时，他们张成的空间只有一个点——原点。

向量与点

考虑由 \(\hat{\imath}\) 和 \(\hat{\jmath}\) 张成的空间，易知是整个二维平面。但是如果我们要把每一个向量都在图中用箭头的形式画出来，那就会占满整个坐标系，不方便观察。

将向量抽象成点，就是解决这个问题的方法。

因为向量默认从原点出发，所以我们可以不需要画出原点，只需要画出终点。画出向量 \(\vec{v}=\begin{bmatrix}\ x\ \\\ y\ \end{bmatrix}\) 在图中其实只需要画出点 \((x,y)\) 就可以表示这个向量了。

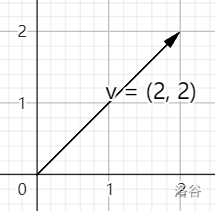可以表示成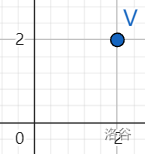

那么这无数个向量就可以表示为无数个点，组合起来就是整个平面了。

同理，如果张成的空间是一条直线，我们也可以理解为无数个向量表示的点都在这个直线上，组合起来就是一条直线。

三维向量张成的空间

先考虑三维空间中两个向量张成的空间。

和二维中很像，如果共线，那么就是一条直线，都是零向量就只在原点。否则就是一整个平面。

接下来加入第三个向量，下面默认前两个向量都不是零向量且不共线。

如果第三个向量在原来两个向量张成的平面中，那么加入这个向量不会对最终张成的空间产生贡献。也就是说，加上这个向量后，张成的空间依旧是那个平面。

否则就是整个三维空间。

可以这样去考虑。如果第三个向量不在原平面中，那么将它缩放，就可以经过整条直线。而这个向量的缩放移动，带来的是整个原平面的移动。一个无限大的平面，上下移动无限长的距离，整个平面扫过的地方就是整个无限的三维空间。

线性相关\(\text{(Linearly Dependent)}\)

考虑 / 两个二维向量共线 / 或 / 第三个三维向量 / 处在 / 前两个向量张成的平面上。

• / 为断句。

那么我们拿走一个向量，剩余向量张成的空间仍然不会改变，那我们就称这几个向量是线性相关的\(\text{(Linearly Dependent)}\)。

反之，拿走一个向量会让张成的空间少一个维度，那我们就称这几个向量是线性无关的\(\text{(Linearly Independent)}\)。

思考题的证明

先看题

张成该空间的一个线性无关的向量集

用反证法，原命题中共两个重点：张成该空间、线性无关。

\(1.\) 张成该空间

如果这个向量集不能张成该空间，那么它一定不是该空间的一个基。否则它不能形成这这个空间。

\(2.\) 线性无关

以二维空间为例。如果两个向量线性相关，那么他们张成的就是一条直线，而不是一个平面。

本章总结

单位向量、线性组合、张成的空间、线性相关立即关于思考题的想法。