第15课——递归的应用实战一汉诺塔、全排列等
递归的数学思想

递归的数学表示

斐波拉契数列递归解法
 View Code
View Code
运行结果:

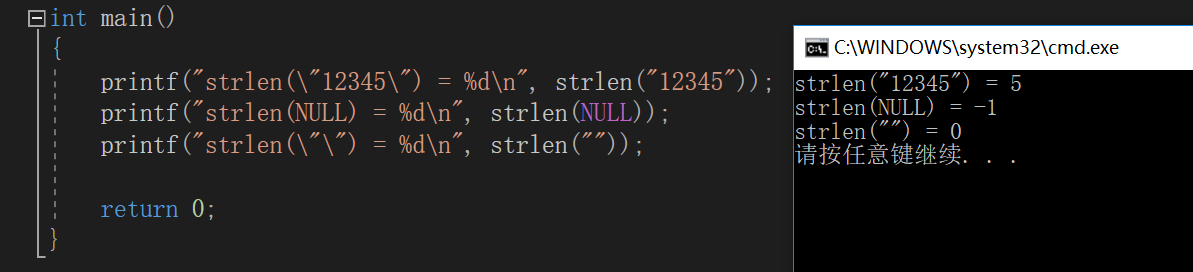
strlen 递归解法
 strlen
strlen
运行结果:
汉诺塔递归解法
递归当然只能以递归的思路理解,把它展开纯属自讨苦吃。
递归思路,说白了是如下三步:
1、对于问题N,如果N-1已经解决了,那么N是否很容易解决。
2、一步步递推下去,终究会有个“包工头”,接到“搬第一层”的任务。
3、既然第一层搬了,那么第二层当然就可以搬了;第二层搬了,第三层又可以搬了……依次类推,直到第N层。于是问题搞定。
这一步就是“回归”。
如上三步加起来,就是“递归”。
推而广之,任何问题,不管规模为N时有多复杂,只要把N-1那块“外包”给别人做之后,我们在这个基础上可以轻易完成N,那么它很可能就适合用“递归”解决。
那么,怎么最终确定它能不能用“递归”做呢?
看当N取1或2之类最简情况时,问题是否可以解决——然后写程序解决它。
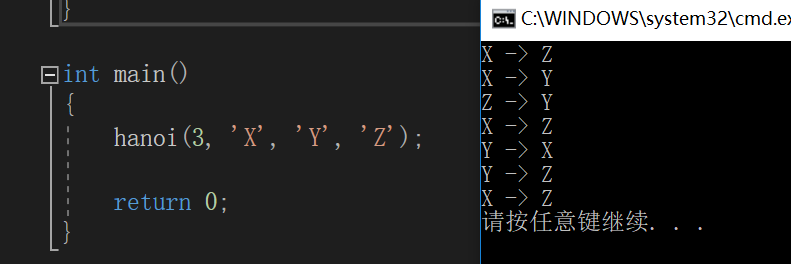
 View Code
View Code运行结果如下:
全排列递归解法
全排列函数:
 View Code
View Codemain函数及运行结果
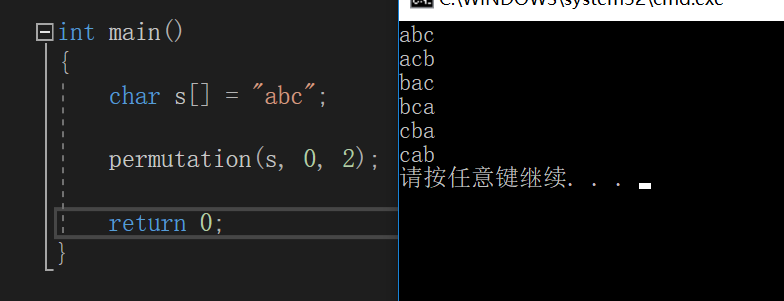
“abc”传入全排列函数,首先b=0;‘a’和自身交换,剩下的“bc”进行全排列,
然后是“ab”交换位置,b在前,“ac”进行全排列,把交换后的“bc”还原。
最后“ac”交换位置,c在前,“ba”进行全排列,把交换后的“ac”还原。
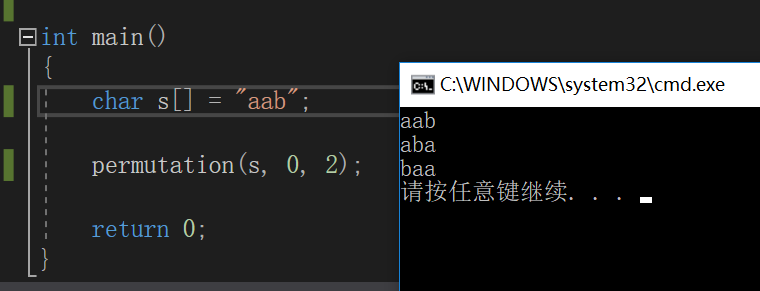
修改全排列元素:为"abb"
运行结果如下:
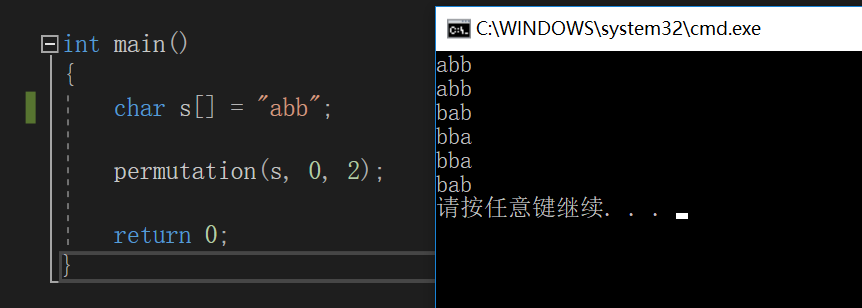
可以看到,全排列的结果有重复,此排列函数不能处理有重复元素的全排列。
怎样修改代码呢?
当判断到重复的元素后就不交换,即要执行交换,必须当前的两元素不同才交换。
修改代码为:
 View Code
View Code运行结果如下:
小结:

posted on 2019-12-05 13:52 blogernice 阅读(122) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号