21201417-裴建航-BLOG-2

前言：

　　　　这次blog是对pta的第四次，第五次以及期中考试的题目进行总结分析。本次blog主要是对pta-4的凸四边形的计算，pta-5五边形的相关计算以及期中考试类的设计，继承与多态的分析。首先pta-4的凸四边形考察四边形的判断成立条件，四边形的分类，凹凸四边形的判断，在输入输出上几乎和上次的三角的题目一样，值得一提的是多了除冗余点。该题的题目量不大，但是难度还是挺高的，知识点上和前面的三角形的知识相差不大。然后是pta-5考察对五边形的判定，凹凸五边形的判断，以及相关计算问题。输入输出上与四边形相同。最难的点在于后一题的输入点构成两个图形的位置关系。期中考试的题目相对pta的图形题较简单。主要考察类的设计，多态与继承的利用，新的容器类的创建。刚好是对期中考试前几周的知识的利用。难点在于多态的使用与表达不是很会用，再者对于抽象类的使用还不是很熟悉，不清楚抽象类的用处。下面具体的分析各题目。

 

 

设计与分析：

　　　　　　首先分析一下期中考试的题目：（如下）

　　　　　　　　　　　　　　　　　　　　　　　　　　7-1 点与线（类设计）

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息，输出格式如下：

• 

   

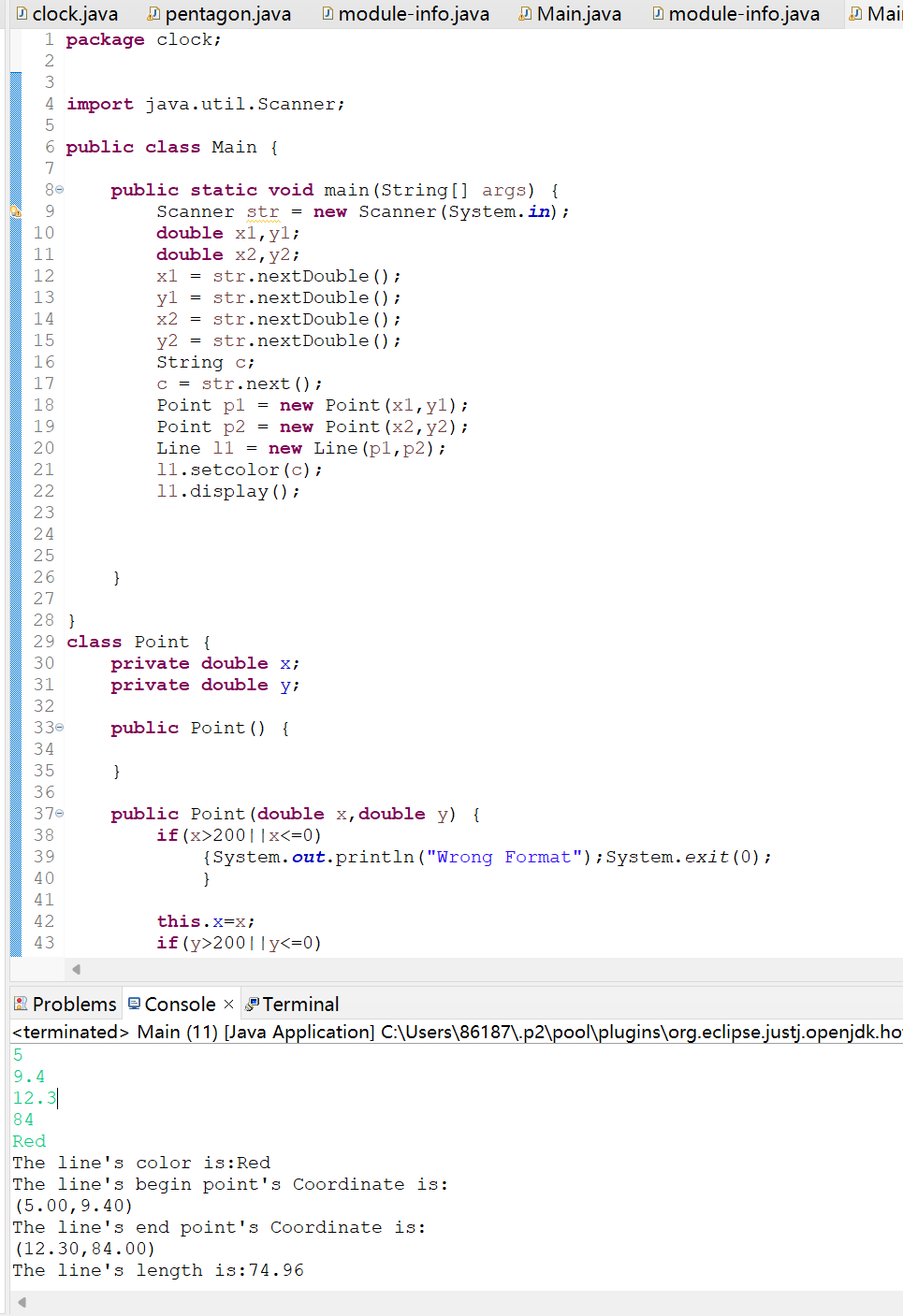
   计算两点之间的距离，先定义好一个Point类，point类有点的横坐标从坐标为私有属性，不得不用到settter，getter，方法对点坐标进行调用与赋值，注意一点输出的距离必须格式化，还得设计以Line的类计算其长度，定义好类之后的计算其实没有难度了。考察的知识点就是对类的理解，对面向对象的理解。

• 第二题：
• 　　　　　　　　7-2 点线面问题重构（继承与多态）

• 在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
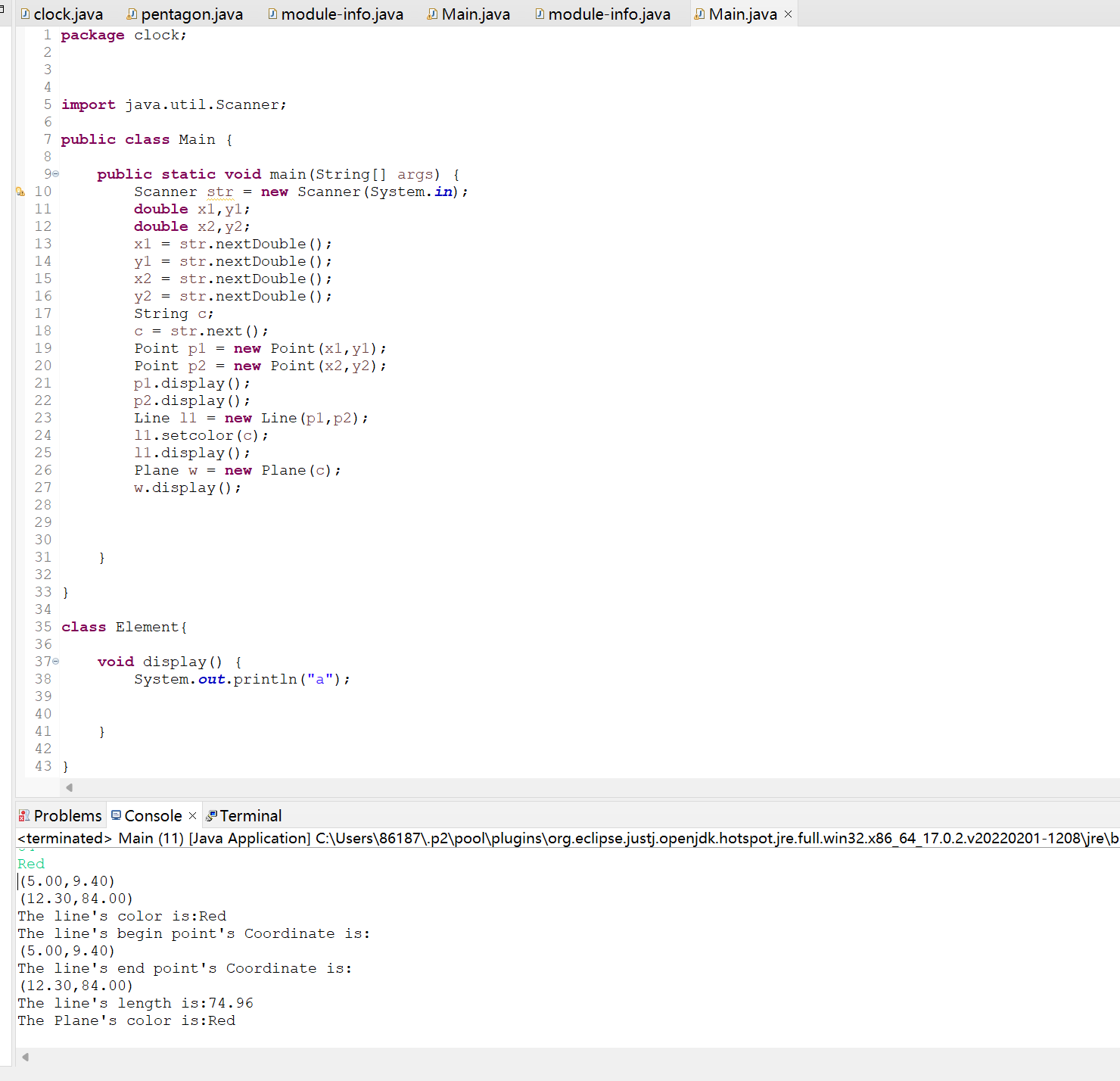
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。示例代码如下：

        element = p1;//起点Point
        element.display();
        
        element = p2;//终点Point
        element.display();
        
        element = line;//线段
        element.display();
        
        element = plane;//面
        element.display();

 

　　　　　　在第一题的基础上增加了对继承与多态的认识，难点在与需要定义一个抽象类Element作为父类，Plane，Line，Point他们有着共同的属性color，和共同的方法getter，setter，display等所以在父类的定义上给了我们提示，不同的地方是display的方法在不同的子类中是不同的，需要自己来定义。在表达display可以用到多态的方式来，父类中也有一个display的方法但是没有具体的定义，为一个抽象类。

　　

 

 　　　　第三题：

　　　　　　　　　　　　　　　　　　　　　　　　　　　　7-3 点线面问题再重构（容器类）

　　　　　　

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束
  示例代码如下：

     choice = input.nextInt();
      while(choice != 0) {
          switch(choice) {
          case 1://insert Point object into list 
            ...
              break;
          case 2://insert Line object into list
              ...
              break;
          case 3://insert Plane object into list
              ...
              break;
          case 4://delete index - 1 object from list
              int index = input.nextInt();
              ...
          }
          choice = input.nextInt();
      }

　　　　　　

　　　　在第二题的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象，增加该类的add()方法及remove(int index)方法。容器类中包含了Point，Line，Plane对象，难点在与对这些对象的增加与删除对象，然后分类进行操作。

 

 

下面是对pta-4，pta-5题目的分析与总结：（因为pta-4，pta-5都是对图像的设计与计算有许多的共同点，所以放在一起分析。）

 

 

　　pta-4：　　　　　　　　　　　　　　　　　　7-2 点线形系列4-凸四边形的计算

　　　　

 

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

 

pta-5：　　　　　　　　　　　　　　　　　　7-1 点线形系列5-凸五边形的计算-1

 

 

　　　　　　

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

 

　　　　　　　　　　　　　　　　　　　　7-2 点线形系列5-凸五边形的计算-2

 

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

 

不难看出这几题的有许多的相同点，如输入输出都是一样的。图形题都需要定义point类，Line类，所以可以使用相同的。两种类型都需要判定四边形五边形的成立条件，也需要判断凹凸四边形的情况，可以使用叉乘法来判断。每一题中都有相关的面积与周长的计算，然后难点在与第三题的输入十个点，需要判断形成的是五边形四边形三边形，分类的情况太多。输入十个的点判断形成的两个图形是什么并且计算是否有重叠部分，计算出重叠部分的面积。这部分的知识点有一点超出了我的能力。需要分类的情况太多了，根本也就不知道重合的部分怎么计算出来，重合的部分不确定是什么图形。第六问的判断第一点是否在后五个点形成的五边形之中。在第三题的五边形的判断中，五边形的判定条件不是很清楚，有几个测试点还是过不去。

 

 

 

 

 

 

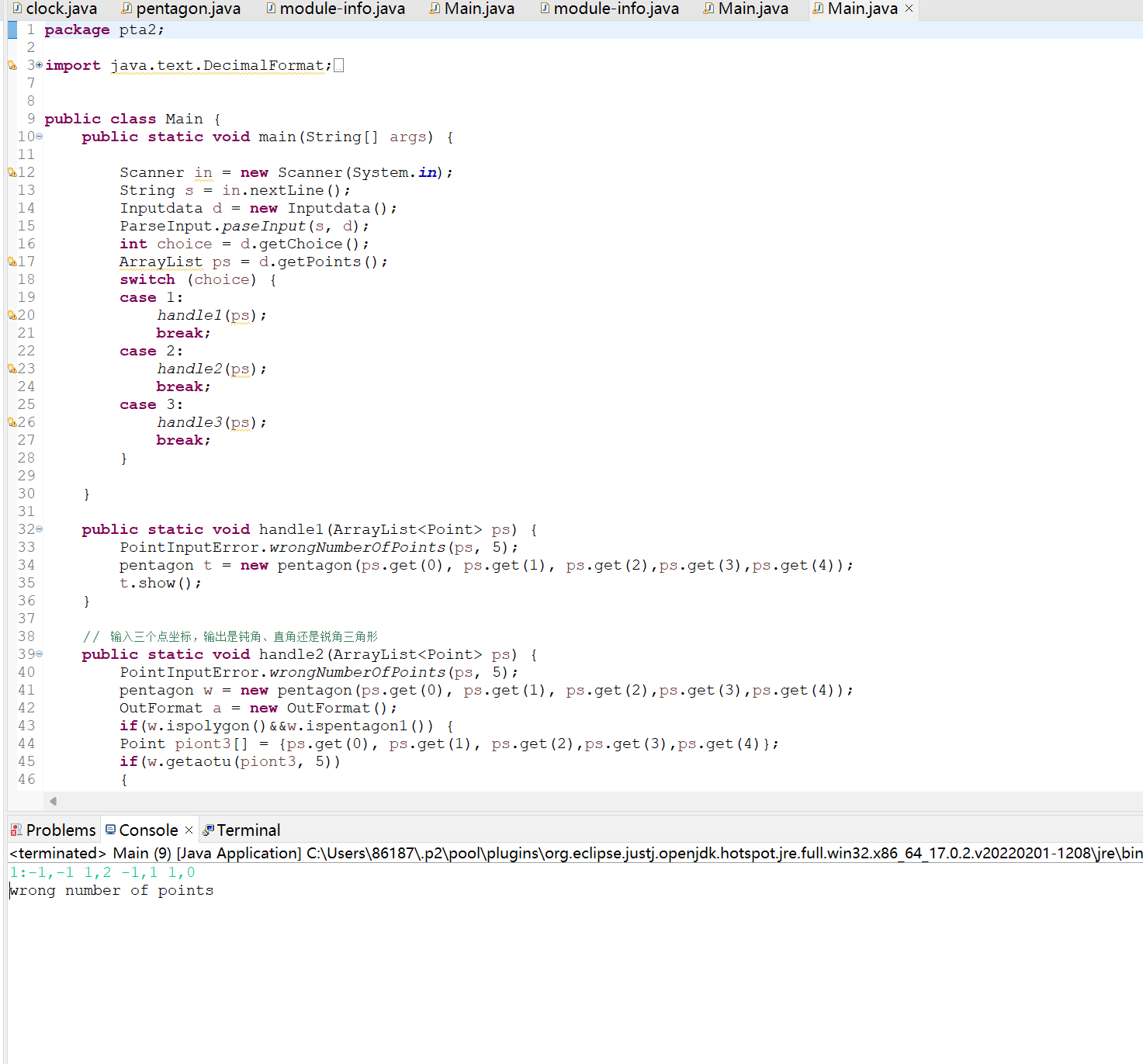
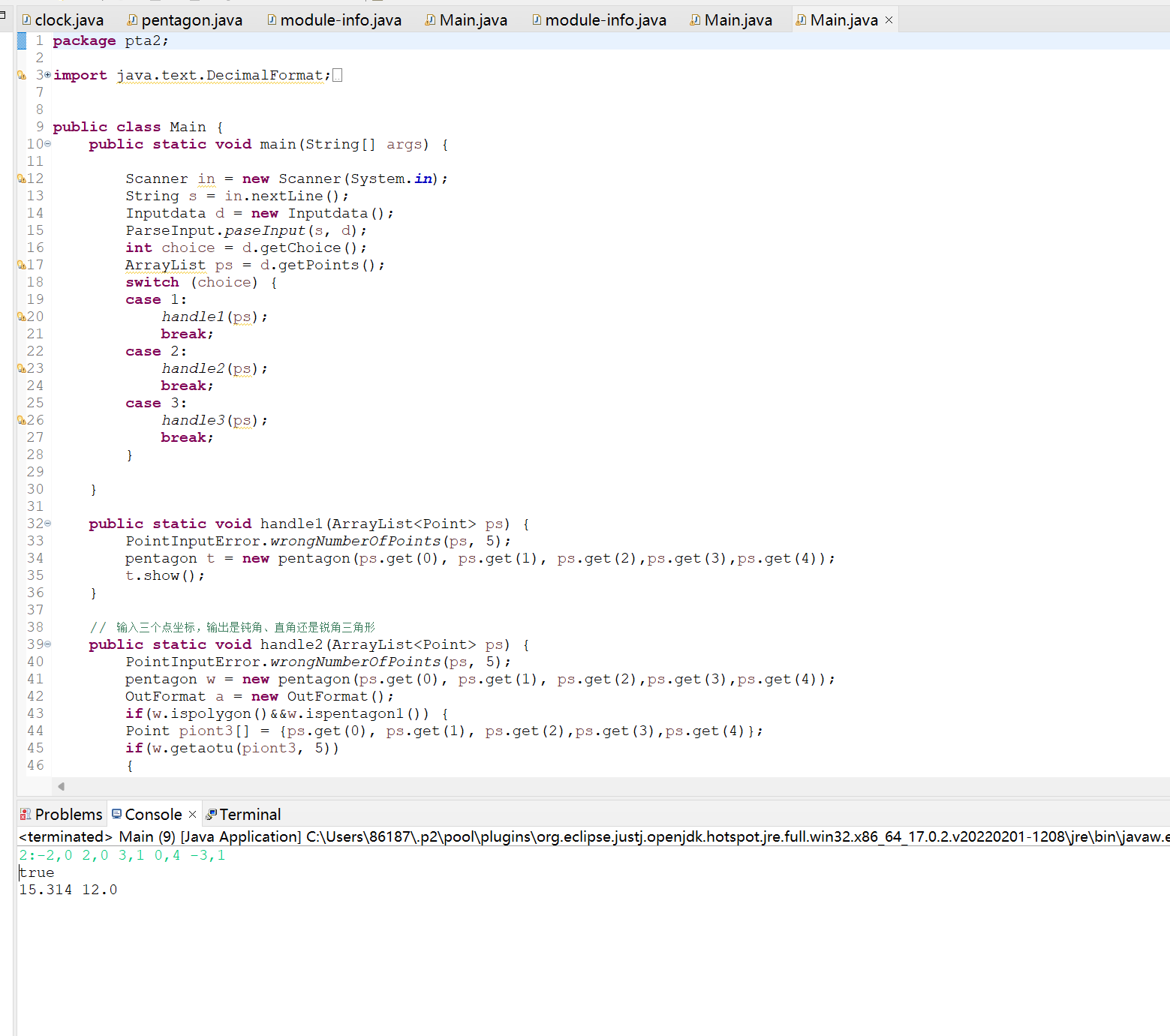
踩坑心得：1：对于多态的理解与使用不是很清楚，父类中定义抽象类如何使用和相关知识点不懂。

　　　　　2：凹凸多边形判断，我使用的是叉乘法，但是我并不清楚原理是什么，我是在百度上查找的别人的方法。在这过程中，尝试过角度法，然后不是很清楚原理是什么，一次一次尝试之后选择换方法。

　　　　　3：在line的定义中，忽视了输入的两个点是会重合的情况，这样不能构成line，所以这里有bug，导致我之后在五边形的判定上，五边形的长度计算上有漏洞。

　　　　　

 

 

改进与总结：1：在判断凹凸多边中，我通过查找百度发现了叉乘法，我成功的解决了这个问题。但是我不知道它的原理是什么只知道折磨用。在接下来几天我得花时间好好的去看看，去了解更　　　　　　                      多的方法来判断凹凸多边形。

　　　　　　

　　　　　　2：我觉得我在类的设计上存在盲目性，不知道该去创建什么样的类，该有怎样的方法与属性。类和类的关系是怎样的。