线段树
何谓线段树
又是一个长时间没用的数据结构,复杂而又简单的线段树,简单是思路简单,复杂是调起来复杂(起步一个下午)
线段树及其强大的东西,可以在 \(\operatorname O(4\log n)\) 时间内完成,区间修改(增删改减),区间查询的操作 ,即所有关于区间的操作,它都能以 \(\operatorname O(4\log n)\) 的时间完成。相当于大砍刀,什么都能用。
线段树内每一个节点都存有一个区间[l, r]的信息,只有一个root根节点即全区间,每个父节点后有两个子节点,分别存有两个子区间的信息[l, mid]与[mid + 1, r],这两个子区间严丝合缝,且占满整个父区间。
一颗线段树大体长这样
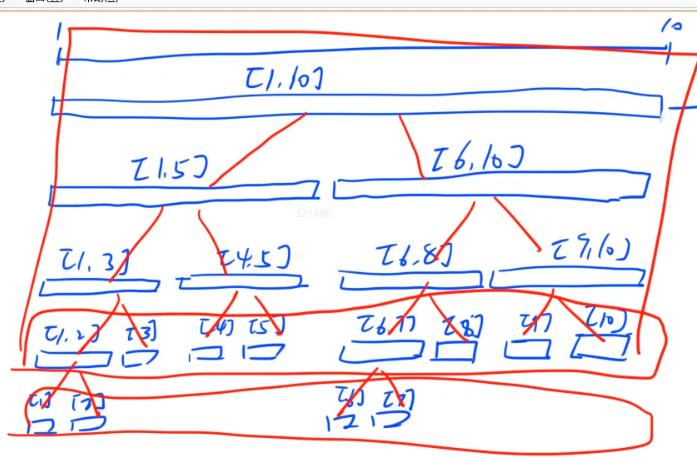
一颗合格的线段树,应支持,建立,修改,查询等基本操作
存储线段树
一般线段树的节点我们用结构体来存储,比较方便使用。
如何建立父子关系
- 分析线段树,可以发现是一颗满二叉树,那么可以沿用堆的存储方式,设父节点为u,则左右儿子分别为
u * 2和u * 2 + 1,也可以写成u << 1和u << 1 | 1的形式,这样通过儿子通过除2就可以找到父节点,父节点可以通过上面的u << 1和u << 1 | 1找到子节点 - 我们可以通过记录父子关系,在结构体内直接记录左右儿子的下标,直接查询。
一般结构体长这样
struct Node
{
int l, r; // 左右端点
区间信息
// int ls, rs; // 左右儿子下标(用第一种存储方式的话,不用这句话)
}tr[N * 4];
线段树一般开4倍空间。因为线段树是一个满二叉树,所以这个二叉树第N - 1行一定是满的,考虑所有叶节点最多有n个,而第N - 1行可以放叶节点,所以第N - 1行最多有n个节点,那么从1~N - 1行一共2n - 1个节点(二叉树性质),那么第N行最多就是2n个,那么总共大约是4n个节点,也就是四倍空间。
在时间上常数很大,可以考虑为 4 ~ 8,当然很多时候往往不止这些,上个20应该都没事。所以要学会用 [[树状数组(待补)(生硬 公式 用法 证明)|树状数组]]。
建立线段树(build)
首先要认识一点,线段树不能扩增,建完了就是建完了,不能扩增。
意思是大小是一开始定义好的,比如存1~1000的区间,那么以后就只能在这个区间内进行。
那我们要添加东西怎么办?直接建好一个大的,把添加操作当成修改就行了。
所以建立线段树,上来就要全部建好。
代码
void build(int u, int l, int r) // 初始化
{
if (l == r) tr[u] = {l, r, ... }; // 如果建立到单个元素,则直接赋值
else
{
int mid = l + r >> 1;
tr[u] = {l, r}; // 先给这个点赋值l, r, 也可以更多
build(u << 1, l, mid); // 建立左儿子
build(u << 1 | 1, mid + 1, r); // 建立右儿子
pushup(u); // 用儿子更新u点
}
}
上面出现了pushup后面会写到
利用子节点更新父节点(pushup)
pushup操作相比pushdown(利用父节点更新子节点)更简单些。
用于建树和修改中,且都应当进行pushup操作(有特例)。
这东西随着题目不同,用法不同,但亘古不变的是它是用来更新父节点信息的。
代码
常见的如这样(记录区间最大值)
void pushup(int u)
{
tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1]. v);
// 由子节点的信息,来计算父节点的信息
// tr[u].l = tr[u << 1].l;
// tr[u].r = tr[u << 1 | 1].r;
}
常用用法
这里列举一下常用用法
多个pushup
有的时候我们厌烦些tr[u].l等,也为了增加代码的实用性,pushup有时候会写两个。
像这样(下面代码是计算区间最大连续字段和的代码)
void pushup(Node &u, Node &l, Node &r)
{
u.ssum = max({l.ssum, r.ssum, l.rsum + r.lsum});
u.l = l.l;
u.r = r.r;
u.sum = l.sum + r.sum;
u.lsum = max(l.lsum, l.sum + r.lsum);
u.rsum = max(r.rsum, r.sum + l.rsum);
}
void pushup(int u)
{
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
利用C++的重载函数,写两个pushup,方便使用,像在build()中我直接pushup(u),即可
而在其他函数中,我可能要合并两个节点信息,这时候调用第一个pushup即可,可以很好的减少码量和错误率。
利用父节点更新子节点(pushdown)
pushdown又名懒标记。思想非常nb,对于区间修改如果我们每个都修改,那么时间太大了,
这时候可以在一个区间上打上一个标记,表示它的子区间修改状态为,这里以区间加为例。
如果想在[1, 6]内加上d,那么我们可以给满足在这个区间内的节点都加上add的懒标记,并修改sum等参数,注意如果一个节点被当前d标记过了,那么它的子节点不用现在标记,
等到要用子区间时再下传标记即可。这样本来O(n)的算法就优化为了O(logn)
这里说几个常用懒标记的写法
区间加 add
void pushdown(Node &u, int add)
{
u.sum += (u.r - u.l + 1) * add;
u.add += add;
}
void pushdown(int u) //可以写两个pushdown,上面的那个还可以用于区间修改,增加代码灵活性
{
pushdown(tr[u << 1], tr[u].add);
pushdown(tr[u << 1 | 1], tr[u].add);
tr[u].add = 0;
}
首先下传完标记后,要清空当前标记。对于区间加,我们设sum为区间和,因为这一个区间都加上了add,一共加了r - l + 1个数,所以sum增加应为(r - l + 1) * add
区间乘
void pushdown(Node &u, int mul)
{
u.sum = u.sum * mul;
u.mul = u.mul * mul;
}
void pushdown(int u)
{
pushdown(tr[u << 1], tr[u].add);
pushdown(tr[u << 1 | 1], tr[u].add);
tr[u].mul = 1;
}
注意一点,区间乘mul初始化和清空都为1。因为是区间乘,直接乘整个区间即可。
对于有多个懒标记的情况要分析下传先后顺序
如区间乘和区间加同时存在时要先遵循先乘后加,这是由分析得来的。
建议这部分自己想想
当懒加(add)和懒乘(mul)同时存在, 我们先计算懒乘后懒加
因为 sum * mul + add == sma // sma == 's'um * 'm'ul + 'a'dd
sma + c = sum * mul + (add + c);
sma * k = sum * mul *k + add * k;
mul * k -> mul', add * k -> add'
sma = sum * mul' + add'
我们发现是可行的
如果sam == (sum + add) * mul
sam + c == (sum + add) * mul + c
这时候我们发现没法记录先乘还是先加没法化成 sam形式
所以使用sma形式
修改(modify)
你做题可能会遇到区间修改和单点修改两种情况,but,单点修改不就是区间修改的特殊情况吗?所以记住一个区间修改即可。不必写两个函数,实际上,大部分情况,我们写一个修改函数就可以完成任何类型的修改操作。
注意,modify时pushdown和pushup应当都进行
代码大概长这样
void modify(int u, int l, int r, int add) // 这里的l, r指修改区间, add为添加的数
{
if (l <= tr[u].l && tr[u].r <= r) pushdown(tr[u], add); // 修改tr[u]值
else // 实际上这里的pushdown是前面的重载的写法是为了减少码量增加代码灵活性
{ // 请看前面 pushdown 的重载以明白这里干了个什么
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if (l <= mid) modify(u << 1, l, r, add); // 如果左区间有,我就去修改左区间
if (r > mid) modify(u << 1 | 1, l, r, add); // 同理搞右区间
pushup(u);
}
}
注意这里面的l, r和build函数里的l, r含有不一样,是目标区间。
一般线段树的修改函数的结构都是一样的,只不过是pushdown和pushup的不同罢了
关于这两句话
if (l <= mid) modify(u << 1, l, r, add);
if (r > mid) modify(u << 1 | 1, l, r, add);
注意是不可能出现 r < tr[u].l 或者 l > tr[u].r 的情况的,也就是说当前区间一定是和目标区间有交集的。从开始看,区间包含整个序列,也肯定包含目标区间,这时候有三种情况(黑色表示当前区间,红色是目标区间,可以交到边界):
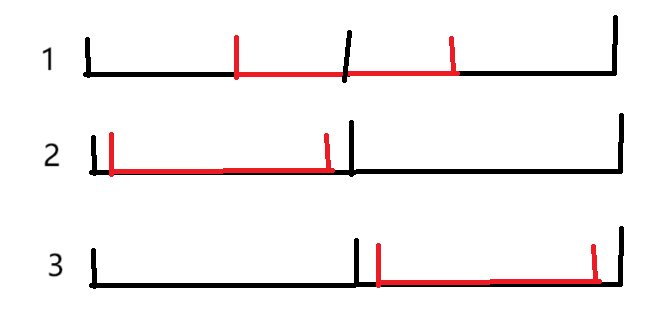
本质上 2,3 是一样的,而对于 1,进入子树后,当前区间(子树)与目标区间的交集的边界(即红虚线),就会和当前区间的边界至少有一个相同,即如下:
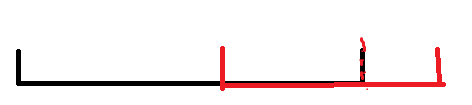
那么以后的进入的每一个区间都至少和目标区间有相同边界,如果有两个边界,则直接返回区间值,如果只有一个边界,本质上就像 1 一样。
而对于 \(2,3\) 终究也会变成 1 的类型。因此当前区间一定是和目标区间有交集的。这句话适用于修改函数,也适用于查询函数等只要用这类方法的函数。
这两句话也就是正确的。即我已经知道了我和它有交集,然后左/右边还有它,那么我就去左/右。
modify中pushdown的原因
如果不下传那么当modify时会用子节点来更新父节点的值(pushup),如此,因为懒标记没下传,子节点的值不是真实值,因此更新的父节点的值就会错误,导致修改的错误
常用技巧
这是一个奇技淫巧
有时候很会遇到仅区间加的情况,这时候可以不用懒标记,通过套一个差分数组,就可以实现区间修改,当然查询的时间复杂度也会增加,但对于某些,如区间最值等,这东西非常好用了
查询(query)
查询操作,线段树有且仅有的使用方式,你可以区间查询也可以单点,怎么玩都行
关于返回值,还是比较建议直接返回一个节点,这样你一个询问函数,就可以利用这个节点查出所有你想要的东西。
一般长这样
Node query(int u, int l, int r)
{
if (l <= tr[u].l && tr[u].r <= r) return tr[u];
else
{
pushdown(u); // 注意查询的时候是需要pushdown的原因写在下方
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r); // 区间全部在左
else if (l > mid) retrun query(u << 1 | 1, l, r); // 全部在右
else // 左右都有
{
Node ls = query(u << 1, l, r);
Node rs = query(u << 1 | 1, l, r);
Node res;
pushup(res, ls, rs); // 合并节点
return res;
}
}
}
query中pushdown的原因
如果不下传标记,那么子节点的值就不是真实值,查出来的也就不是正确答案,因此要pushdown
可以不pushup,如果不放心,pushup一下也没错。因为查询形式上不改变子节点,所以pushdown之后 u 的值就是pushup之后的值。
更多技巧
线段树建图
比如用线段树建图?
Legacy - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这题虽然是紫色,但是就是一个线段树建图的模版
线段树上二分
线段树的奇幻科技——线段树上二分 - Mercury_City - 博客园 (cnblogs.com) 这篇博客讲的好,但仍不详细。
不是二分+线段树,是直接利用线段树去二分查找。从而把 \(O(\log^2 n)\) 变为 \(O(\log n)\)。
基本原理是直接利用当前的左子树和右子树,去判断目的解是在左还是右,然后直接进入有解的子树。而对于限制区间,只需要按正常查询的思维,只去与目标区间相交(包括在之内的情况)的区间。因为如果这个区间不完全包含在目标区间内,那么提供的信息就不准确,所以要到完全包含的区间内提供信息。看了代码应该就理解这句话了。
我研究了得一天,下面给出我测试所用的代码包,和这个优化的效果。
一个基本的例题是查找区间 \([1,n]\) 内第一个大于 \(x\) 的数的下标。按照意思可以写出以下代码:
int query(int u, int x)
{
if (tr[u].l == tr[u].r) return tr[u].l;
else
{
int mid = l + r >> 1;
if (tr[u << 1].maxv > x) return query(u << 1, l, r, x); // 如果左边有就直接去左边
else return query(u << 1 | 1, l, r, x); // 否则一定在右边
}
}
但是这会导致一个问题,即如果不存在这样的数,我们没法表示出,所以要表示无解情况,一般以 -1 作为无解情况。即:
int query(int u, int x)
{
if (tr[u].l == tr[u].r)
{
if (tr[u].maxv <= x) return -1;
return tr[u].l;
}
else
{
int mid = l + r >> 1; // 多余了
if (tr[u << 1].maxv > x) return query(u << 1, l, r, x);
else return query(u << 1 | 1, l, r, x);
}
}
每次要么去左边要么去右边,所以时间复杂度一定 \(O(\log n)\)。
如果限制区间为 \([l, r]\) 呢?按照上面说的,如果有限制区间,那么当前区间和限制区间的关系就分为相交,被包含和不相交。对于不相交,我们就不进入子树,而对于相交,只要相交就进入对应子区间,因为要利用相交的那部分的信息。实际上这部分和正常 query 一样。
对于包含则进行上面那样的二分。如果到了对应节点就返回信息。实际上对于不相交的情况,我们不用管他,只进行相交的进入子树即可。
于是可以写出以下代码
int query(int u, int l, int r, int x)
{
if (tr[u].l == tr[u].r) // 找到一个解
{
if (tr[u].maxv <= x) return -1; // 去除无效解
return tr[u].l;
}
else if (l <= tr[u].l && tr[u].r <= r) // 可以提供信息
{
if (tr[u << 1].maxv > x) return query(u << 1, l, r, x);
else return query(u << 1 | 1, l, r, x);
}
else // 仅相交,要继续划分区间,直到被包含
{
int mid = tr[u].l + tr[u].r >> 1;
int res = -1;
if (l <= mid) res = query(u << 1, l, r, x); // 去含有的区间内, 和正常query一样
if (res == -1 && r > mid) res = query(u << 1 | 1, l, r, x);
return res;
}
}
整体思路就是,正常 query 进限制区间,在区间内二分,直到有解返回。
二分是可以封边界的,上面代码就封左边界,即找尽量靠左的符合条件的点。对于封左/右边界,你只需要让它趋于进入左/右子树即可。给出对应封右的代码。
int query(int u, int l, int r, int x)
{
if (tr[u].l == tr[u].r)
{
if (tr[u].maxv <= x) return -1;
return tr[u].l;
}
else if (l <= tr[u].l && tr[u].r <= r)
{
if (tr[u << 1 | 1].maxv > x) return query(u << 1 | 1, l, r, x); // 尽量先进右子树
else return query(u << 1, l, r, x);
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
int res = -1;
if (r > mid) res = query(u << 1 | 1, l, r, x); // 同理
if (res == -1 && l <= mid) res = query(u << 1, l, r, x);
return res;
}
}
测试文件: https://pan.axianyu.cn/f/3vqFn/线段树二分.zip
例题
来做做例题把,我费劲自己搞得 U502676 线段树上二分模版 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
常见问题
MLE
注意修改和查询的范围,如果范围超过了线段树范围有可能会 MLE,爆栈。包括小于和大于。
一个线段树多次使用
多次使用同一个线段树,区间起始长度 \([1, n]\) 不能改变。你可以只利用其中一段。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号