VSLAM笔记——2. 特征提取与匹配 — FAST和BRIEF

之前在对极几何里，我们说到，只要找到两个图像的八对对应点，就能从中恢复出相机的运动了（2D-2D的对极几何八点法），但是怎么找到两个对应点呢？其中一个思路就是特征点提取与匹配。

这其中有很多种提取和匹配的方法，这里先说说比较经典的FAST特征点和BRIEF描述子吧。

想象一下，给出两张图，我们人类很容易就能分辨出两张图里，哪些部分是同一个物体在不同视角下拍摄的，也能大概感觉出两张图像之前的运动关系，比如下面这两张图，我们很轻松的就能感觉到：右边的图，相比左边的图，视角更偏向右边一点。

可是计算机要如何分辨这种运动呢？在之前的内容里我们知道了可以通过2D-2D的对极几何，其实还有通过空间三维点和当前图片对应点来计算的PnP求解方法（3D-2D），或者通过两组对应的空间三维点来计算的ICP方法（3D-3D），然而这些方法都绕不开一个问题：如何判断两张图像上的对应点（想起PnP和ICP的坑还没填QAQ）。

1. 思想

如果想判断两张图像的对应点，首先要解决的就是我们怎么从图像中，找到这样的一个点。

比如两张图里有很多的猫（怎么又是猫），我们如何区分两张图里，哪些猫是同一只呢？

“可以通过花色，胖瘦，毛的长短呀！”

这就是一个很好的思路，对于图像也是，要判断两张图中的对应点，它们得有一些“信息”来帮助我们判断：

• 它需要是一个比较“特别”的点，如果图里的猫长得都一模一样我们就很难判断了
• 它要在两幅图像内都能被看到，并且不应该变形很多，如果猫在第二张图里跑掉了，甚至变色了（？），那我们也很难判断
• 要能区分出它与另一张图像的哪个点是对应的，即便这只猫在第一张图里很有特点，在第二张图里跑过来几只和它一样的猫，我们也很难判断

于是人们发现，角点似乎是一种很好的特征点，同一颜色区块内的点，由于长得都一样，不够有“特点”，无法判断。

边缘线上的点，虽然有些“特别”了，但是沿线所有的点和它都一样，也无法判断。

而角点，我们可以很容易的分辨出来。

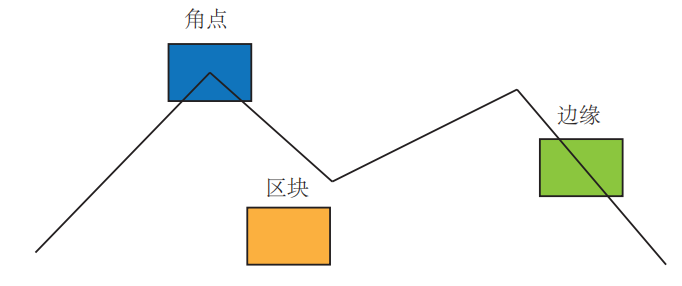
所以我们要想一个办法，来检测出图像中的角点，然后再另一张图像中寻找与之匹配的对应点。

2.FAST特征点

FAST（Features from Accelerated Segment Test）就提供了这样一种判断角点的方法，比如这个窗子上的点，判断它是一个角点，应该满足这样的条件：

• 图像上某一个像素点p的亮度为I_p。
• 设置一个阈值T。
• 以p为圆心，选择半径为3的圆上的16个点。
• 如果这些点中有连续N个点的亮度＞I_p+T，或＜I_p-T，则认为p是一个角点。

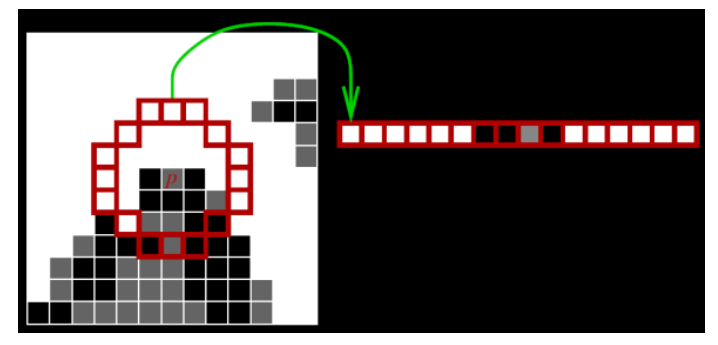
在实际算法里，我们可以先检测其中的第1、5、9、13点，如果它们之中有三个（FAST-12）同时满足条件，才可能是一个角点，这样就能排除很多非角点了。

另外比如上面的图中，p的左右，上下相邻的点实际上也满足FAST角点的条件，但是实际上这个地方我们只需要标记一个角点就可以了，这时候还需要使用非极大值抑制（NMS），选择出p附近（比如5x5的窗口内）所有被判定为角点的点中，响应值最大的点作为最终的结果。

响应值根据下面这个公式计算：

\[V = max\left\{\begin{matrix} \Sigma(I_{i} - I_{p}),if(I_{p}<I_{i})\\ \Sigma(I_{p} - I_{i}),if(I_{p}>I_{i}) \end{matrix}\right. \]

其中I_i是判定角点时的连续N个点的亮度值。也就是说，角点和周围点的亮度差距越大，它的响应值就越高。

3.BRIEF描述子

通过FAST，我们知道了怎么从图像中判断出一个角点（特征点），但是当我们要和另外一个图像的特征点匹配时，我们还缺乏一种手段，来描述它们两个是不是相似的，有多相似。

这时候就需要描述子啦，BRIEF（Binary Robust Independent Elementary Features）就提供了一种对特征点的描述手段。

它的思想是，在特征点p附近，S*S大小的像素块内，随机选取一对点a和b。

对比这两个点：

\[f(a,b) = \left\{\begin{matrix} 1 \qquad if(I_{a} < I_{b}) \\ 0 \qquad otherwise \end{matrix}\right. \]

然后选取下一对点重复，假设一共有n对点，把所有点的结果组成一个二值串（可以看做没对点的结果占一个二进制数的一位）：

\[result = \sum_{i = 0}^{n}2^{i-1}f(a,b) \]

这样我们就得到了这个特征点p的BRIEF描述子。

---

实际上原论文里，对于应该选取多少对点，随机选取点对应该如何随机，都做出了试验，比如随机选取点对，他们尝试了：

• 在像素块内平均采样选取（G I）

• a,b从（0， S²/25）的正态分布内采样（G II）

• a从（0， S²/25），b从（0， S²/100）的正态分布内采样 （G III）

• 在空间量化极坐标下离散随机采样 （G IV）

• a固定为像素块中心，b在周围平均采样 （G V）

几种方法，最终发现第二种效果最好，先在（0， S²/25）内随机生成n对（2n个，常见n = 128, 256 512）点，然后接下来固定这些点对坐标来对每个特征点计算生成n维的BRIEF描述子。

---

这样我们就通过特征点p附近的n对点构建了一个n维的BRIEF描述子，它的形式是一个n位的二进制数，对于另一张图的特征点，我们只需要按位比较他们的BRIEF描述子，通过计算不同处的个数，就能计算出他们之间的汉明距离，从而判断它们之间的匹配程度啦！

4.总结

FAST提供了一种特征点检测的方法，它通过计算某一点与周围点的关系，检测出角点来提取图像的特征点，进而提供了特征点的“位置”。

而BRIEF则提供了一种描述特征点自身属性的方法，它通过特征点周围的n个随机点对，构建了一个二进制的描述子，进而描述特征点的“样貌”。

但是提取FAST特征点 + 计算BRIEF描述子这一组合，没有解决下面几个问题：

• 尺度不变：当某个物体的一点在较远处可以认为是角点时，在较近处不一定是角点，反之同理。（想象下飞机上俯瞰汽车，和在面前停着的汽车）。

• 旋转不变：提取到的某个特征点，在旋转后，与原特征点无法匹配。

虽然有SIFT特征点+SIFT描述子的组合，可以解决这些问题，但是其计算的成本太大（包括后续的SURF），无法用在SLAM这样的实时系统里，那么，有没有一个……

当然有！那就是接着FAST + BRIEF这一组合继续下去的ORB特征啦！