VSLAM笔记——1. 我们如何通过图像来计算位置的变化：2D-2D的对极几何

想当初就看了好多次高博的《十四讲》，不过当时感觉天书一样，不说看了没能理解的，还有理解了最后又忘了的。
到现在接触视觉SLAM也有一年多了，也尝试过跑别人的开源算法，试着自己写简单的SLAM，总觉得《十四讲》里的讲解顺序并不太适合学习，开头的硬核数学部分，当时着实是差点劝退了我。
正好最近需要好好把这些东西都整理，复习一下，我就按照我自己的理解，以及我觉得比较好的顺序来说说VSLAM吧....

0.复习下相机模型以及各种坐标转换

对于一个三维空间点P(X, Y, Z)，根据相机的成像原理，我们能知道，它与对应的图像上的点的像素坐标(u, v)会有这样的对应关系：

\[\left\{\begin{matrix}u = f_{x}\frac{X}{Z} + c_{x} \\ v = f_{y}\frac{Y}{Z} + c_{y}\end{matrix}\right. \]

这个关系可以写成矩阵的形式，这样以后可以更方便表示和计算。

\[Z\begin{pmatrix}u\\ v\\ z\end{pmatrix} = \begin{pmatrix}f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y}\\ 0&0 &1 \end{pmatrix}\begin{pmatrix}X\\ Y\\ Z\end{pmatrix} = KP \]

其中K是相机的内参，它在相机制造后就已经确定了，我们可以通过相机标定来获取它。

借用高博的图来说，这样对于P(X, Y, Z)来说，就像这样：

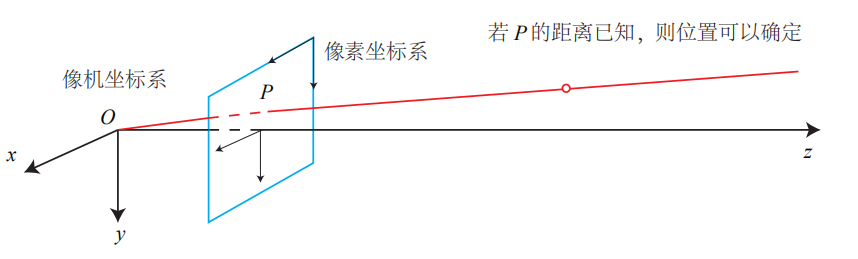
我们可以从P点的三维坐标，通过相机内参矩阵，很容易的算出它在图像上投影点的像素坐标。

但这并不是我们在VSLAM中想要关注的地方，我们想要关注的地方正相反：

如何在知道图像上某点p(u, v)的像素坐标的情况下，算出它所对应的点P在三维空间中的坐标(X, Y, Z)。但是再看一下三维坐标与像素坐标的对应关系：

\[\left\{\begin{matrix}u = f_{x}\frac{X}{Z} + c_{x} \\ v = f_{y}\frac{Y}{Z} + c_{y}\end{matrix}\right. \]

我们就会发现一个问题：我们已知了像素坐标u，v，已知了相机内参，我们也只能求得X，Y与Z的比值，既X/Z和Y/Z，并不能直接求出来XYZ的具体值。

对于上面高博的图来说，红色连线上所有的点，都会投影在同一点p(u, v)上，那应该是哪个位置的点呢？

1.对极几何

上面说了通过一张图像，我们很难知道对应的三维空间点到底在哪，于是有人想到了这样的办法：

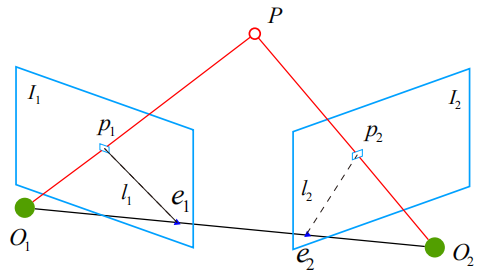
“我们再加一个相机，或者移动一下换个角度，这样两张图片红色线的交叉点不就是P点的空间位置了嘛！”

在这张图里，p1和p2是三维空间点P分别在两张图像上的投影点，射线O₁p₁和射线O₂p₂是点P可能的空间位置。

我们把O₁O₂P组成的平面称为极平面，O₁O₂称为基线，而O₁O₂和两个图像平面的交点e₁和e₂称为极点，极平面与图像平面的相交线称为极线。

再整理一下我们目前未知量，和已知量：

未知的：点P的位置，第二次拍照，或者第二个相机的位置O₂

我们已知的：两个像平面的点p₁和p₂... 呃，这好像什么都不知道嘛。

从直观上来想，如果我们已知了O₁和O₂的空间位置，我们就能很轻松的知道两条红线在哪里交叉，也就能求出点P的空间位置。

那么反过来如果我们已知了点P和相机O₁的空间位置，我们能求出相机O₂的位置吗？

答案是可以。

这就是视觉SLAM的想法了，我们试着来推导一下。

相机O₂是从相机O₁的位置运动来的，我们把这个运动，拆分成旋转和平移两部分，分别用R和t来表示。

假设点P的三维坐标为：

\[P = [X,Y,Z]^{T} \]

那么它和两个像平面的投影p₁和p₂，应该满足下面的关系，其中K依然表示相机内参：

\[Zp_{1} = KP, Zp_{2} = K(RP+t) \tag{1} \]

这时候我们要开始做一个非常有意思的操作了，既然前面我们通过像平面点p(u, v)，只能求出X/Z、Y/Z，那我们不妨设Z=1，相当于在相机前方Z=1处设立了一个平面，那么根据之前的公式，这个平面上的点，与p(u, v)应该有这样的关系：

\[Z\begin{pmatrix} v\\ u \end{pmatrix} = KP = K \begin{pmatrix}X\\ Y\\ Z\end{pmatrix} \]

两边同时处以Z：

\[\begin{pmatrix} v\\ u \end{pmatrix} = KP = K \begin{pmatrix}X/Z\\ Y/Z\\ 1\end{pmatrix} \]

整理：

\[\begin{pmatrix}X/Z\\ Y/Z\\ 1\end{pmatrix} = K ^{-1}\begin{pmatrix} v\\ u \end{pmatrix} = K ^{-1}p \]

这样我们的到了一个点(X/Z, Y/Z, 1)和像平面点p(u, v)的关系，我们之前设立的Z=1的平面，被称为归一化平面，而(X/Z, Y/Z, 1)这是空间点P在这个平面上的投影，我们设这个投影点为x，于是我们可以知道，P在两个相机的归一化平面点x₁、x₂, 与像平面点p₁、p₂存在这样的关系：

\[x_{1} = K ^{-1}p_{1}, x_{2} = K ^{-1}p_{2} \]

将它带入式（1），能得到：

\[x_{2} = Rx_{1} + t \tag{2} \]

我们由t，可以得到一个它的反对称矩阵t^（参考李群李代数部分）：

\[t = [t_{1},t_{2},t_{3}]^{T}\\t ^{∧} = \begin{pmatrix}0 & -t_{3} & t_{2}\\ t_{3} & 0 & -t_{1}\\ -t_{2} & t_{1} & 0\end{pmatrix} \]

将式（2）两边同时左乘t^，然后再左乘x₂^T，得到：

\[x_{2}^{T}t^{∧}x_{2} = x_{2}^{T}t^{∧}Rx_{1} \]

实际上，左乘t^{**就相当于和**t**做外积，而**t}x₂是一个同时与t、x₂相垂直的向量，因此上式等号左边为0，即：

\[x_{2}^{T}t^{∧}Rx_{1} = 0 \]

我们再把p₁和p₂带入回来：

\[p_{2}^{T}K^{-T}t^{∧}RK^{-1}p_{1} = 0 \]

这时候我们发现：神奇的事情发生了！我们现在不需要知道P点的空间位置，也不需要真正利用归一化平面，只需要知道p₁和p₂，即两张图上，同一点的像素坐标，以及相机的内参矩阵K，就可以求解两张图之间相机的运动R、t了！（虽然目前还有一小点点障碍）

我们把中间的部分，记作两个矩阵：本质矩阵E、基础矩阵F，则有：

\[E = t^{∧}R , F = K^{-T}EK^{-1}\\x_{2}^{T}Ex_{1} = p_{2}^{T}Fp_{1} = 0 \]

可以看出，本质矩阵E、基础矩阵F的差距只有相机内参K，而K是可以通过相机标定获得的，两个矩阵求出一个就能求出另一个，而这两个矩阵就包含着我们想要求解的相机运动R、t。

所以我们接下来的目标便是求解出其中一个矩阵。

2.本质矩阵E的求解

上面说过，本质矩阵E、基础矩阵F，得其一我们就可以求解相机运动了。

比如ORBSLAM是通过基础矩阵F来求解的，既然是根据《十四讲》整理的笔记，这里就用高博书上的办法，通过本质矩阵E，来求解相机运动吧。

我们再来看一下刚才得到的结论：

\[x_{2}^{T}Ex_{1} =0 \]

其中x₁、x₂是点P在对应的两个相机的归一化平面的坐标，为了方便描述，我们使用x₁ = [u₁, v₁, 1]^T的形式来表示它，E则是我们需要求解的本质矩阵，我们这样表示：

\[E = \begin{pmatrix}e_{1} & e_{2} & e_{3}\\ e_{4} & e_{5} & e_{6}\\ e_{7} & e_{8} & e_{9}\end{pmatrix} \]

于是之前的式子变成这样：

\[\begin{pmatrix}u_{2},v_{2},1 \end{pmatrix} \begin{pmatrix}e_{1} & e_{2} & e_{3}\\ e_{4} & e_{5} & e_{6}\\ e_{7} & e_{8} & e_{9}\end{pmatrix} \begin{pmatrix}u_{1}\\v_{1}\\1 \end{pmatrix} = 0 \tag{3} \]

这个方程还是不太好看，既然我们需要求解的是E中的各个值，我们不妨把E展开，写成向量的形式：

\[e = [e_{1},e_{2},e_{3},e_{4},e_{5},e_{6},e_{7},e_{8},e_{9},]^{T} \]

那么刚才的(3)式可以改写成线性形式的：

\[[u_{1}u_{2},u_{1}v_{2},u_{1},v_{1}v_{2},v_{1},u_{2},v_{2},1]e = 0 \]

看起来有点脑壳疼，不过其实就是把之前的(3)式乘完后整理的样子。如果我们有N对点，第i对点我们用uⁱ，vⁱ来表示，那么有：

\[\begin{pmatrix}u_{1}^{1}u_{2}^{1}&u_{1}^{1}v_{2}^{1}&u_{1}^{1}&v_{1}^{1}u_{2}^{1}&v_{1}^{1}v_{2}^{1}&v_{1}^{1}&u_{2}^{1}&v_{2}^{1}&1 \\ u_{1}^{2}u_{2}^{2}&u_{1}^{2}v_{2}^{2}&u_{1}^{2}&v_{1}^{2}u_{2}^{2}&v_{1}^{2}v_{2}^{2}&v_{1}^{2}&u_{2}^{2}&v_{2}^{2}&1 \\ \vdots & \vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots &\vdots \\ u_{1}^{n}u_{2}^{n}&u_{1}^{n}v_{2}^{n}&u_{1}^{n}&v_{1}^{n}u_{2}^{n}&v_{1}^{n}v_{2}^{n}&v_{1}^{n}&u_{2}^{n}&v_{2}^{n}&1\end{pmatrix}\begin{pmatrix}e^{1}\\ e^{2}\\ e^{3}\\ e^{4}\\ e^{5}\\ e^{6}\\ e^{7}\\ e^{8}\\ e^{9}\end{pmatrix} = 0 \tag{4} \]

这下就变成线性方程的形式啦！我们现在的目标就是求解这个线性方程，从而求得本质矩阵E。那么我们需要几对点，才能求出E呢？

从本质矩阵E的定义以及性质来看：

• E包含的平移t以及旋转R各自有三个自由度，所以E应该具有六个自由度。

• 然而，E由一个等式为0的对极约束定义，E在乘以任何非零常数时，式（3）依旧成立，这是E的尺度不定性，由直觉来思考，由于归一化的操作，平移t和其k倍的kt对于等式都可以成立，比如我们解出t = [1,1,1]，这里的“1”我们并不能确认它代表1米还是1千米或者什么。

  所以实际上，本质矩阵E只有五个自由度。

于是，理论上，我们可以通过五对点来求解本质矩阵E，然而由于E的非线性，我们很难通过五个点就求解出E，于是我们选择上面公式（4）的方法，求解出E（不过这样做还会有一些其他的问题）。

我们注意到，式（4）也是等于零的，它一样具有尺度不定性，比如把等式两边同时除以e⁹，那么我们需要求解的量的减少了一个，所以我们需要至少8对点来求解本质矩阵E，这就是八点法（Eight-point-algorithm）。

接下来，我们要做的就是从求得的本质矩阵E中，恢复相机运动的平移t以及旋转R。

3.相机运动恢复——奇异值分解（SVD）

感觉这部分高博讲的不是很清楚，找资料整理再顺畅的讲出来，快吐血了

整个思路很神奇，有点绕，我们回顾一下本质矩阵E的定义：

\[E = t^{∧}R \]

其中的t^是由平移向量t生成的一个反对称矩阵，根据其性质我们可以把这个反对称矩阵表示成这样的形式：

\[t^{∧} = kUZU^{T} \tag{5} \]

其中的U，是一个正交矩阵，k是一个实数，Z是下面这个矩阵：

\[Z = \begin{pmatrix}0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix} \]

可能你会问，式（5）真的成立吗？我们来推一下，我们设U为：

\[U = \begin{pmatrix}u_{1} & u_{2} & u_{3}\\ u_{4} & u_{5} & u_{6}\\ u_{7} & u_{8} & u_{9}\end{pmatrix} \]

那么式（5）可以写成

\[kUZU^{T} = \begin{pmatrix}u_{1} & u_{2} & u_{3}\\ u_{4} & u_{5} & u_{6}\\ u_{7} & u_{8} & u_{9}\end{pmatrix}\begin{pmatrix}0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix}\begin{pmatrix}u_{1} & u_{4} & u_{7}\\ u_{2} & u_{5} & u_{8}\\ u_{3} & u_{6} & u_{9}\end{pmatrix} \]

计算一下可得：

\[kUZU^{T} =k\begin{pmatrix}0 & u_{1}u_{5}-u_{2}u_{4}& u_{1}u_{8}-u_{2}u_{7}\\ u_{2}u_{4}-u_{1}u_{5} & 0 & u_{4}u_{8}-u_{5}u_{7} \\ u_{2}u_{7}-u_{1}u_{8} & u_{5}u_{7}-u_{4}u_{8} & 0\end{pmatrix} \]

正是一个反对称矩阵，说明我们的式（5）是成立的，这样我们就把求解t^转化成了求解U，所以我们要如何找到这样一个U呢？

答案是奇异值分解（SVD）。

我们回顾一下特征值分解，如果有一个mxm的实对称矩阵A，那么这个A可以被分解为这种形式：

\[A = QΣQ^{T} \]

其中Q是标准正交阵，其列向量为A的特征向量，Σ是一个只有主对角元素非零，且对角线元素是由大到小排列的A的特征值的对角矩阵。

这个例子中，矩阵A比较特殊，如果我们有一个一般性的矩阵，是否也能做类似的操作呢？这就是奇异值分解。对于一个mxn的实数矩阵A，我们进行奇异值分解，可以得到：

\[A = UΣV^{T} \]

分解的结果，我们得到了mxm的矩阵U和nxn的矩阵V，它们都是正交矩阵，而中间的Σ则是一个mxn的，仅在主对角线有值的矩阵，我们称这些值为奇异值。

对于原矩阵与分解结果，又有这样的关系：

\[AA^{T}=UΣV^{T}VΣ^{T}U^{T}=UΣΣ^{T}U^{T}\\A^{T}A=VΣ^{T}U^{T}UΣV^{T}=VΣ^{T}ΣV^{T} \]

这两个式子和上面的特征值分解形式上非常相似，并且AA^T，A^TA分别是mxm，nxn的两个对称矩阵，ΣΣ^T，Σ^TΣ也分别是mxm，nxn的，只有主对角线有值，且值为A的奇异值的矩阵。

于是我们可以发现，对AA^T，A^TA分别做特征值分解，求出的特征矩阵就分别为U和V^T了！

于是我们尝试对本质矩阵E做奇异值分解，我们可以得到：

\[E = UΣV^{T} \]

然后通过上面的方法求出其中的U、Σ和V^T。可是这有什么用呢？我们再回过头看看本质矩阵E，平移t，旋转R的关系：

\[E = t^{∧}R \\t^{∧} = kUZU^{T}\\>> E = kUZU^{T}R \]

其中的Z，我们引入一个正交矩阵W，来把它做一下变形：

\[Z = \begin{pmatrix}0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix} = diag(1,1,0)\begin{pmatrix}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 1\end{pmatrix} = diag(1,1,0)W \]

其中的diag(1,1,0)，表示一个只有主对角线有值，且分别为1,1,0的3x3矩阵，于是本质矩阵E变成这样：

\[E = t^{∧}R = kUZU^{T}R = kUdiag(1,1,0)WU^{T}R \]

我们来观察这个式子，其中k由于E的尺度不定性，可以去掉。W、U^T、R，都是正交矩阵，他们的组合也是一个正交矩阵，我们记作V^T，于是：

\[E = t^{∧}R = Udiag(1,1,0)V^{T}\tag{6} \]

对比一下上面关于E的奇异值分解结果：

\[E = UΣV^{T} \]

两个式子的U和V^T，均是3x3正交矩阵，diag(1,1,0)和Σ均是仅有主对角线有值的3x3矩阵，那是不是说，我们只要把本质矩阵E，进行奇异值分解，就可以得到式（6）中的U和V^T了呢！！

现在唯一的疑问，就是diag(1,1,0)和Σ是否对应，其实我们是能够证明，本质矩阵E是具有两个相等奇异值的矩阵，并且由于E的尺度不定性，我们完全可以将两个奇异值设为1，具体可以参考下面的连接。

SVD分解与矩阵的迹

这样我们终于找到了这样一个神奇的方法：

• 本质矩阵E，平移t，旋转R的关系，其实就是将E进行奇异值分解后的结果。

• 进而我们可以通过分解后的U，求出平移t^。

  \[t^{∧} = kUZU^{T} \]

• 最后通过我们自定的w，分解出的V^T，求得旋转R

  \[V^{T} = WU^{T}R \]

  但是这里还有一个问题，就是通过U来表示t^时，我们设定的Z：

  \[Z = \begin{pmatrix}0 & 1 & 0\\ -1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix} or Z = \begin{pmatrix}0 & -1 & 0\\ 1 & 0 & 0\\ 0 & 0 & 0\end{pmatrix} \]

  都能满足要求（实际上是E的分解有diag(1,1,0)和diag(-1,-1,0)两种情况），这就造成了我们最终求得的t^共有两种，对应的R，也有两种，共计四组解：

  \[t^{∧}_{1} = kUdiag(1,1,0)WU^{T}\\t^{∧}_{2} = kUdiag(-1,-1,0)WU^{T} \]

  这四组解实际上分别是这四种情况：

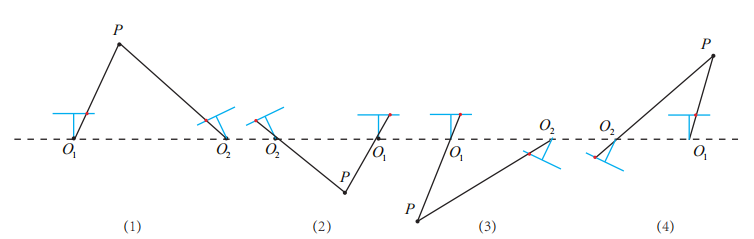
我们都知道三维点P的深度，只可能大于零，所以最后我们也能正确筛选出正确的解。

总结：

• 通过对极几何，我们能了解到，两张图像上对应点p₁和p₂，以及与相机的旋转R，平移t存在这样的关系：

  \[p_{2}^{T}K^{-T}t^{∧}RK^{-1}p_{1} = 0\\E = t^{∧}R , F = K^{-T}EK^{-1}\\x_{2}^{T}Ex_{1} = p_{2}^{T}Fp_{1} = 0 \]

• 其中的本质矩阵E，可以通过找到两张图中，8对两两对应的图像点，通过八点法求解得出

• 而本质矩阵E，通过奇异值分解（SVD），可以求解出旋转R以及平移t

由此我们知道了如何从两幅图像，恢复相机的运动，而VSLAM的一大思想，就是通过图片，求出图与图之间的位姿变化（R、t），即求出本质矩阵E和基础矩阵F，不过在这里，我们事先假设了我们已知两幅图像上，哪两个点是互相对应的，于是接下来我们的问题就转化成：如何找到两张图像的对应点啦！

思考:

1.对极几何求解相机位姿，是2D（图像）到2D（图像）的，我们仍然未知图像点对应的空间点P的位置，它可能在相机光心与图像点连线（那条红色线）的任意一处上，为了解决这个问题，我们可以使用RGBD相机来直接获取P的深度，或者采用三角化的方法，来获取对应点的深度。实际上对于RGBD相机或者双目相机，有更好的求解相机位姿的方法，比如对于RGBD相机我们可以通过3D-3D的ICP求解，或者3D-2DPnP求解，但是他们都需要知道空间点P的位置，而对于单目相机而言，不知道相机的运动就无法算出P的位置（无法三角化求解），进而也无法用ICP或者PnP求解相机运动，这似乎就成了鸡生蛋，蛋生鸡的问题了，所以单目相机是需要通过对极几何来进行初始化的，然而初始化也并非对极几何这么简单，如果后面我有空整理单目相机初始化的部分再叙述吧。
2. 在求解本质矩阵E时，我们采用了八点法，那么如果图像中的配对点，多余8个，或者存在错误匹配的情况，要怎么解决呢？如果我们的匹配点，多与8个，那很有可能由于构建出了一个超定方程，导致无解。这时候可以通过最小二乘来求出一个最小二乘意义下的本质矩阵E。当存在错误匹配时候，我们也可以通过随机采样一致性(RANSAC)的方法来处理错误匹配。
3. 想到再补充