关于平衡树
两种简单的平衡树
前言
\(Q:\) 为什么是两种
\(A:\) 因为我只看了两种
前面丢的是关于二叉查找树的一些性质和操作 (但我没写过也不会写二叉查找树) 来源于一本通提高篇 不想看略过即可
另外 刚开始学 如果发现有写的不准确或者直接错误的地方劳烦指出
\(update\): 2021.3.17 补充 文艺平衡树
二叉查找树 (\(BST\))
先补一下二分查找树的相关
二叉查找树的性质:
- 树种每个节点被赋予了一个权值
- 若左子树不空 则左子树上所有节点的值均小于他的根节点的值
- 若右子树不空 则左子树上所有节点的值均大于他的根节点的值
- 其左右子树也分别为二叉查找树
二叉查找树常用来维护有序的集合 有序的数集 建立索引或优先队列等
遍历
中序遍历 左 -> 自身 -> 右
查找
- 从根节点开始查找
- 当前节点就是要查找的值 查找成功
- 查找的值小于当前节点 在左子树中继续查找
- 查找的值大于当前节点 在右子树中继续查找
- 当前节点为空 查找失败 即该值在树中不存在
查找最值
最小值:若左子节点不为空 持续访问左子节点 直到为空 当前值即为要找的值
最大值:若右子节点不为空 持续访问右子节点 直到为空 当前值即为要找的值
插入
- 从根节点开始插入
- 如果要插入的值小于当前节点的值 在当前节点的左子树中插入
- 如果要插入的值大于当前节点的值 在当前节点的右子树中插入
- 如果当前节点为空节点 在此建立新节点 该节点的值为要插入的值 左右子树为空 插入成功
- 当插入的值与当前值相同时 在该节点上再加一个值 用于记录这一值的数量
删除
- 该节点为叶子节点 直接删除
- 该节点为链节点 以其子节点代替自身 然后删除
- 该节点有两个非空子节点 以其后继结点的右孩子代替其后继结点 取其后继结点代替当前节点 当前节点的左孩子置为后继结点的左孩子
题目: P3369 【模板】普通平衡树
\(Treap\)
关于 \(Treap\)
\(Treap\) 是在二叉查找树的基础上多维护了一个优先值 或者说是在维护二叉查找树的性质的同时维护了堆的性质
从权值上来看 \(Treap\) 是一棵二叉查找树 从优先级上来看 \(Treap\) 是一个堆
由于我们的优先级是随机赋予的 所以可以防止凉心出题人通过构造数据使二叉查找树退化成链的情况 以保证各种操作实现的时间复杂度(当然 如果你的随机值依旧近乎退化成链 建议去买彩票)
\(Treap\) 的期望深度与操作的递归层数都是期望 \(O(logn)\) 的
\(Treap\) 的实现
\(Treap\) 中的绝大部分操作都可以类比二叉查找树 毕竟没有本质区别
下面以代码解释为主
- 变量的含义
#define ls(x) (t[x].l)
#define rs(x) (t[x].r)
struct node {int l, r, v, size, rnd, w;}t[B];
\(l\) 与 \(r\) 记录该节点的左右孩子的编号
\(v\) 是该点的权值
\(w\) 是该点的数的个数
\(size\) 以该点为根的子树的大小
\(rnd\) 优先级
- 旋转
旋转的目的在于维护堆序
由于没找到图 所以请听我口胡
旋..干脆看代码注释 画个图理解一下吧...说不清楚
void rturn(int &p) {
int y = ls(p);//记录该点的左孩子
ls(p) = rs(y);//以该点的左孩子的右孩子代替该点的左孩子
rs(y) = p;//以该点代替该点的左孩子的右孩子
t[y].size = t[p].size;//传递孩子数量
up_date(p);//更新
p = y;//以该点的左孩子代替该点
}
void lturn(int &p) {//同上
int y = rs(p);
rs(p) = ls(y);
ls(y) = p;
t[y].size = t[p].size;
up_date(p);
p = y;
}
算了 还是加个图吧 感觉自己在扯淡
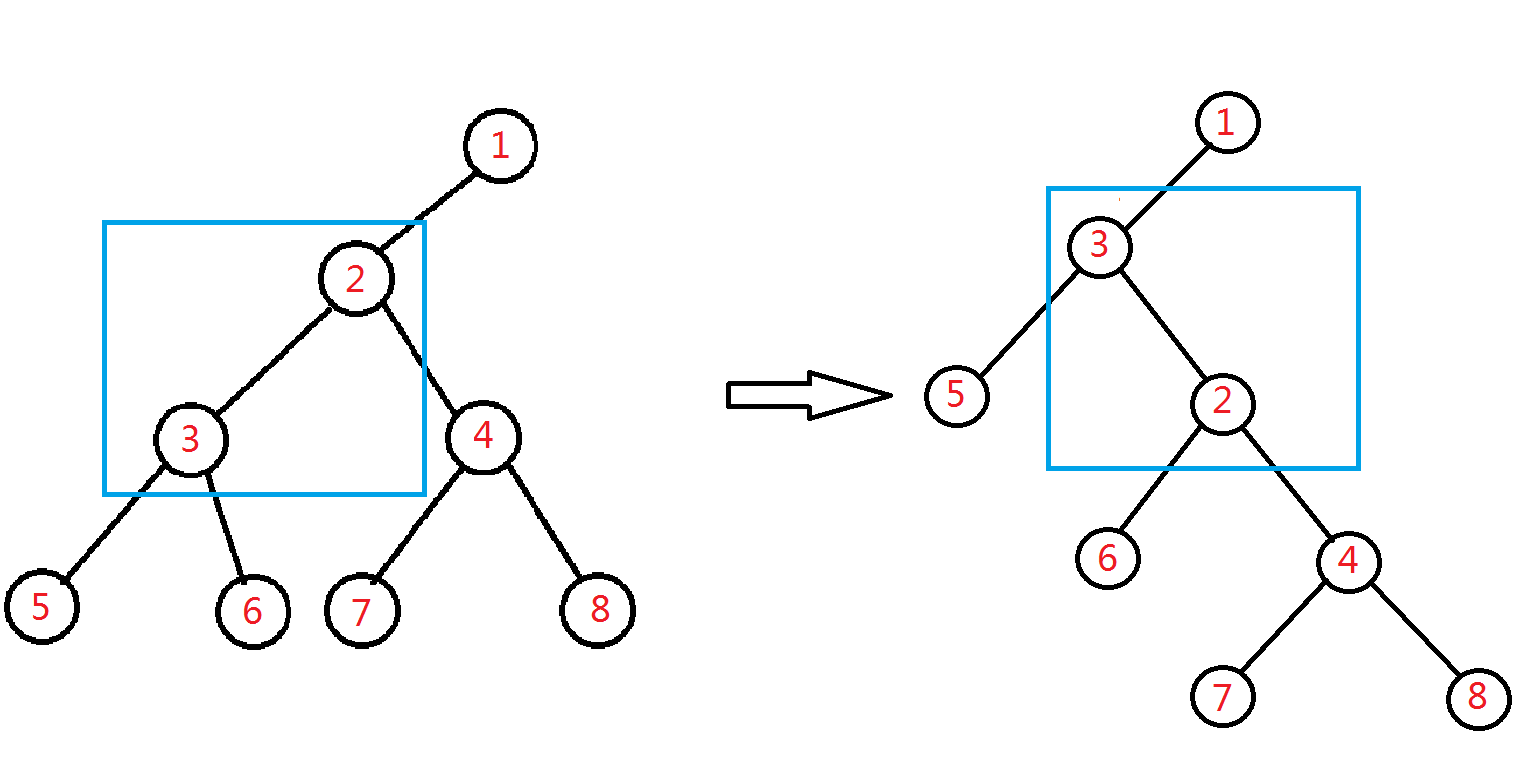
(图是自己画的 挺麻烦 还不好看)
图示为将二号节点右旋的操作 可以对图理解
- 插入操作
void insert(int &p, int x)
{
if(!p) {p = ++cnt; t[p].size = t[p].w = 1; t[p].v = x; t[p].rnd = rand(); return ;}//还没有这个点 新建一个点 并初始化
t[p].size++; if(t[p].v == x) {t[p].w++; return ;}//对于插入路径上的所有点都要维护 size 如果这个点已经有了 记录这个数的次数
if(x > t[p].v) {insert(rs(p), x); if(t[rs(p)].rnd < t[p].rnd) lturn(p);}
else {insert(ls(p), x); if(t[ls(p)].rnd < t[p].rnd) rturn(p);}//比较 向左或向右 同时通过旋转维护堆序
}
- 删除
void del(int &p, int x)
{
if(!p) return ;//不存在
if(t[p].v == x)//找到了~
{
if(t[p].w > 1) {t[p].size--; t[p].w--; return ;}//如果这个数有多个 删一个
if(!(ls(p) * rs(p))) p = ls(p) + rs(p);//只有一个 则如果是叶子节点或链节点 用孩子节点代替该点 相当于删除(如果是叶子结点 子节点是空节点)
else if(t[ls(p)].rnd < t[rs(p)].rnd) rturn(p), del(p, x);//不是叶子或者是链的话 根据左右孩子的堆序 将该点不断旋转 直到成为叶子节点或链节点
else lturn(p), del(p, x);
}
else if(x > t[p].v) t[p].size--, del(rs(p), x);
else t[p].size--, del(ls(p), x);//判断找的方向 一路维护 size的值 毕竟删是一定要删的 一路上的子树大小都会有影响
}
- 查询 \(x\) 的排行
int rank(int p, int x)
{
if(!p) return 0;//空
if(t[p].v == x) return t[ls(p)].size + 1;//找到了 左子树里面的数一定都小于根节点 所以返回左子树的大小加一
if(x > t[p].v) return t[ls(p)].size + t[p].w + rank(rs(p), x);//去右侧找的时候要加上左子树的大小和该点的数
return rank(ls(p), x);//左侧则不用
}
- 查询排行 \(x\) 的数
int num(int p, int x)
{
if(!p) return 0;//空
if(x <= t[ls(p)].size) return num(ls(p), x);//小于左子树的大小 在左子树
if(x > t[ls(p)].size + t[p].w) return num(rs(p), x - t[ls(p)].size - t[p].w);//大于左子树加上该点的数的大小 在右边
return t[p].v;//否则这个点就是
}
- 查前驱
void pre(int p, int x)
{
if(!p) return ;
if(t[p].v < x) _p = p, pre(rs(p), x);//找到一个比要查的数小的点 先记下来 在去右边找
else pre(ls(p), x);//去左边找
}
- 查后继
void suc(int p, int x)//同上
{
if(!p) return ;
if(t[p].v > x) _p = p, suc(ls(p), x);
else suc(rs(p), x);
}
完整代码:
(不要在吐槽缩进的问题了~)
/*
Time: 2.3
Worker: Blank_space
Source:
*/
/*--------------------------------------------*/
#include<cstdio>
#include<algorithm>
using namespace std;
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n, _p, p, cnt;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
namespace Treap {
#define ls(x) (t[x].l)
#define rs(x) (t[x].r)
struct node {int l, r, v, size, rnd, w;}t[B];
void up_date(int p) {t[p].size = t[ls(p)].size + t[rs(p)].size + t[p].w;}
void rturn(int &p) {int y = ls(p); ls(p) = rs(y); rs(y) = p; t[y].size = t[p].size; up_date(p); p = y;}
void lturn(int &p) {int y = rs(p); rs(p) = ls(y); ls(y) = p; t[y].size = t[p].size; up_date(p); p = y;}
void insert(int &p, int x)
{
if(!p) {p = ++cnt; t[p].size = t[p].w = 1; t[p].v = x; t[p].rnd = rand(); return ;}
t[p].size++; if(t[p].v == x) {t[p].w++; return ;}
if(x > t[p].v) {insert(rs(p), x); if(t[rs(p)].rnd < t[p].rnd) lturn(p);}
else {insert(ls(p), x); if(t[ls(p)].rnd < t[p].rnd) rturn(p);}
}
void del(int &p, int x)
{
if(!p) return ;
if(t[p].v == x)
{
if(t[p].w > 1) {t[p].size--; t[p].w--; return ;}
if(!(ls(p) * rs(p))) p = ls(p) + rs(p);
else if(t[ls(p)].rnd < t[rs(p)].rnd) rturn(p), del(p, x);
else lturn(p), del(p, x);
}
else if(x > t[p].v) t[p].size--, del(rs(p), x);
else t[p].size--, del(ls(p), x);
}
int rank(int p, int x)
{
if(!p) return 0;
if(t[p].v == x) return t[ls(p)].size + 1;
if(x > t[p].v) return t[ls(p)].size + t[p].w + rank(rs(p), x);
return rank(ls(p), x);
}
int num(int p, int x)
{
if(!p) return 0;
if(x <= t[ls(p)].size) return num(ls(p), x);
if(x > t[ls(p)].size + t[p].w) return num(rs(p), x - t[ls(p)].size - t[p].w);
return t[p].v;
}
void pre(int p, int x)
{
if(!p) return ;
if(t[p].v < x) _p = p, pre(rs(p), x);
else pre(ls(p), x);
}
void suc(int p, int x)
{
if(!p) return ;
if(t[p].v > x) _p = p, suc(ls(p), x);
else suc(rs(p), x);
}
}
/*----------------------------------------函数*/
int main()
{
n = read();
for(int i = 1; i <= n; i++)
{
int opt = read(), x = read();
if(opt == 1) Treap::insert(p, x);
if(opt == 2) Treap::del(p, x);
if(opt == 3) printf("%d\n", Treap::rank(p, x));
if(opt == 4) printf("%d\n", Treap::num(p, x));
if(opt == 5) {_p = 0, Treap::pre(p, x); printf("%d\n", Treap::t[_p].v);}
if(opt == 6) {_p = 0, Treap::suc(p, x); printf("%d\n", Treap::t[_p].v);}
}
return 0;
}
\(Splay\)
关于 \(Splay\) —— 权值树
同样是平衡树 其维护平衡的方式是不断将需要的节点旋转到根节点 来实现各种操作 码量比 \(Treap\) 要大 而且理解起来稍微麻烦一点 常数也要比 \(Treap\) 大 但似乎更好用的亚子
\(Splay\)(权值树) 的实现
- 变量的含义
#define fa(x) t[x].fa
#define ls(x) t[x].son[0]
#define rs(x) t[x].son[1]
int rt, cnt, st[C], top;//rt根节点 cnt根的编号 st删去的节点 栈指针
struct node {int son[2], fa, w, v, siz;}t[C];//平衡树主体 son 0左 1右孩子 fa父节点 w数的多少 v数的大小 siz以该点为根的子树大小
- 一些小的操作
int fson(int p) {return p == rs(fa(p));}//判断这个点是其父亲的左孩子还是右孩子
void up_date(int p) {t[p].siz = t[ls(p)].siz + t[rs(p)].siz + t[p].w;}//更新该节点的孩子数
- 旋转操作
最关键的两个函数 也是最难解释的两个函数
由于图实在是不想画 所以就gu了
void rotate(int p) {//实现旋转的函数
int fath = fa(p), x = fson(p);//找到该节点的父节点 以及该节点是父节点的左孩子还是右孩子
if(fa(fa(p))) t[fa(fa(p))].son[fson(fa(p))] = p;//如果这个点的父节点不是根节点 以该节点代替其父节点 更新其父节点与他父节点的父节点的关系
fa(p) = fa(fa(p)); t[fath].son[x] = t[p].son[x ^ 1];//更新该节点与其父节点的关系 实际上替换为了父节点的父节点 更新孩子位置
fa(t[fath].son[x]) = fath; t[p].son[x ^ 1] = fath; fa(fath) = p;//...写不清楚...
up_date(fath); up_date(p);//更新该节点以及父节点的孩子个数
}
void splay(int p) {//节点的旋转
for(; fa(p); rotate(p)) if(fa(fa(p))) rotate(fson(p) == fson(fa(p)) ? fa(p) : p);//将 p 点旋转到根节点
rt = p;//rt相当于一个指向根节点的指针
}
- 加点操作
int add(int fath, int x) {//加点
int p = top ? st[top--] : ++cnt;//优先使用释放的空间
fa(p) = fath; t[p].v = x; t[p].siz = t[p].w = 1;//新建节点初始化
return p;//返回新加点的编号
}
- 插入操作
void insert(int p, int fath, int x) {//插入
if(p && t[p].v != x) {insert(t[p].son[t[p].v < x], p, x); return ;}//判断插入的位置(左/右)
if(t[p].v == x) t[p].w++;//找到 插入
if(!p) {p = add(fath, x); if(fa(p)) t[fa(p)].son[t[fa(p)].v < x] = p;}//没有这个数 在其父亲下面新建一个点 并确定其与父节点的关系(左/右)
up_date(p); up_date(fa(p)); splay(p);//更新孩子数量 并将新插入的点旋转到根节点
}
- 删除操作
void clear(int p) {fa(p) = rs(p) = ls(p) = t[p].v = t[p].w = t[p].siz = 0; st[++top] = p;}//删除的节点释放空间 备用
int find(int p, int x) {//找
if(!p) return 0;//该点不存在
if(x < t[p].v) return find(ls(p), x);
if(x == t[p].v) {splay(p); return 1;}//找到 并将这个点旋转到根节点
return find(rs(p), x);
}
void del(int x) {//删除
if(!find(rt, x)) return ;//该点是否存在 存在的话旋转到根节点
if(t[rt].w > 1) {t[rt].w--; up_date(rt); return ;}//该点有多个数
int srt = rt;//记一下原来的根节点
if(!ls(rt) && !rs(rt)) rt = 0;//一个点 直接删
else if(!ls(rt)) rt = rs(rt), fa(rt) = 0;
else if(!rs(rt)) rt = ls(rt), fa(rt) = 0;//只有一个孩子 把孩子提上来 删
else if(ls(rt) && rs(rt))//两个孩子
{
int lmax = ls(rt);//记左子树的根节点
while(rs(lmax)) lmax = rs(lmax);//根据二叉查找树的性质 找左边最大的值
splay(lmax);//把左边值最大的节点转到根节点
rs(rt) = rs(srt); fa(rs(rt)) = rt;//把右子树接过来
}
clear(srt); up_date(rt);//释放空间 更新根节点的孩子数
}
- 查找 \(x\) 的排名
int rank(int x) {//找 x 的排名
insert(rt, 0, x);//把这个值插入 这个值被转到根节点
int res = t[ls(rt)].siz + 1;//左子树的点数 + 1 就是这个数的排名
del(x);//再删掉
return res;
}
- 查找排名 \(x\) 的数
int num(int x) {//找排名 x 的数
int p = rt;//取根节点
while(1)//找
{
if(!p) return -1;//不存在 (没数)
if(ls(p) && t[ls(p)].siz >= x) p = ls(p);//小于左子树的节点数 在左边
else//在右边
{
x -= ls(p) ? t[ls(p)].siz : 0;//减去左边子树的节点数 到右边找
if(x <= t[p].w) {splay(p); return t[p].v;}//小于这个点的数的数量 找到了 把这个点转到根节点
x -= t[p].w; p = rs(p);//不在这里 继续找
}
}
}
- 查找前驱
int pre(int x) {//查前驱
insert(rt, 0, x);//插入 这个点会转到根节点
int p = ls(rt);//取左子树的根节点
while(rs(p)) p = rs(p);//在左子树中往右找 直到最后 也就是找到比根节点小的最大值
del(x);//把插入的点删了
return t[p].v;
}
- 查找后继
int suc(int x) {//查后继 基本同上
insert(rt, 0, x);
int p = rs(rt);
while(ls(p)) p = ls(p);
del(x);
return t[p].v;
}
完整代码:
/*
Time: 2.21
Worker: Blank_space
Source: P3369 【模板】普通平衡树
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#define Max(x, y) ((x) > (y) ? (x) : (y))
#define Min(x, y) ((x) < (y) ? (x) : (y))
/*--------------------------------------头文件*/
const int M = 1e4;
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int FFF = 0x8fffffff;
/*------------------------------------常量定义*/
int n;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
void _min(int &x, int y) {x = x < y ? x : y;}
void _max(int &x, int y) {x = x > y ? x : y;}
void _abs(int &x) {x = x < 0 ? -x : x;}
namespace Splay {
#define fa(x) t[x].fa
#define ls(x) t[x].son[0]
#define rs(x) t[x].son[1]
int rt, cnt, st[C], top;//根节点 根的编号 删去的节点 栈指针
struct node {int son[2], fa, w, v, siz;}t[C];//平衡树主体 son 0左 1右孩子 fa父节点 w数的多少 v数的大小 siz以该点为根的子树大小
int fson(int p) {return p == rs(fa(p));}//判断这个点是其父亲的左孩子还是右孩子
void clear(int p) {fa(p) = rs(p) = ls(p) = t[p].v = t[p].w = t[p].siz = 0; st[++top] = p;}//删除的节点释放空间 备用
void up_date(int p) {t[p].siz = t[ls(p)].siz + t[rs(p)].siz + t[p].w;}//更新该节点的孩子数
int add(int fath, int x) {//加点
int p = top ? st[top--] : ++cnt;//优先使用释放的空间
fa(p) = fath; t[p].v = x; t[p].siz = t[p].w = 1;//新建节点初始化
return p;//返回新加点的编号
}
void rotate(int p) {//实现旋转的函数
int fath = fa(p), x = fson(p);//找到该节点的父节点 以及该节点是父节点的左孩子还是右孩子
if(fa(fa(p))) t[fa(fa(p))].son[fson(fa(p))] = p;//如果这个点的父节点不是根节点 以该节点代替其父节点 更新其父节点与他父节点的父节点的关系
fa(p) = fa(fa(p)); t[fath].son[x] = t[p].son[x ^ 1];//更新该节点与其父节点的关系 实际上替换为了父节点的父节点 更新孩子位置
fa(t[fath].son[x]) = fath; t[p].son[x ^ 1] = fath; fa(fath) = p;//...写不清楚...
up_date(fath); up_date(p);//更新该节点以及父节点的孩子个数
}
void splay(int p) {//节点的旋转
for(; fa(p); rotate(p)) if(fa(fa(p))) rotate(fson(p) == fson(fa(p)) ? fa(p) : p);//将 p 点旋转到根节点
rt = p;//rt相当于一个指向根节点的指针
}
void insert(int p, int fath, int x) {//插入
if(p && t[p].v != x) {insert(t[p].son[t[p].v < x], p, x); return ;}//判断插入的位置(左/右)
if(t[p].v == x) t[p].w++;//找到 插入
if(!p) {p = add(fath, x); if(fa(p)) t[fa(p)].son[t[fa(p)].v < x] = p;}//没有这个数 在其父亲下面新建一个点 并确定其与父节点的关系(左/右)
up_date(p); up_date(fa(p)); splay(p);//更新孩子数量 并将新插入的点旋转到根节点
}
int find(int p, int x) {//找
if(!p) return 0;//该点不存在
if(x < t[p].v) return find(ls(p), x);
if(x == t[p].v) {splay(p); return 1;}//找到 并将这个点旋转到根节点
return find(rs(p), x);
}
void del(int x) {//删除
if(!find(rt, x)) return ;//该点是否存在 存在的话旋转到根节点
if(t[rt].w > 1) {t[rt].w--; up_date(rt); return ;}//该点有多个数
int srt = rt;//记一下原来的根节点
if(!ls(rt) && !rs(rt)) rt = 0;//一个点 直接删
else if(!ls(rt)) rt = rs(rt), fa(rt) = 0;
else if(!rs(rt)) rt = ls(rt), fa(rt) = 0;//只有一个孩子 把孩子提上来 删
else if(ls(rt) && rs(rt))//两个孩子
{
int lmax = ls(rt);//记左子树的根节点
while(rs(lmax)) lmax = rs(lmax);//根据二叉查找树的性质 找左边最大的值
splay(lmax);//把左边值最大的节点转到根节点
rs(rt) = rs(srt); fa(rs(rt)) = rt;//把右子树接过来
}
clear(srt); up_date(rt);//释放空间 更新根节点的孩子数
}
int rank(int x) {//找 x 的排名
insert(rt, 0, x);//把这个值插入 这个值被转到根节点
int res = t[ls(rt)].siz + 1;//左子树的点数 + 1 就是这个数的排名
del(x);//再删掉
return res;
}
int num(int x) {//找排名 x 的数
int p = rt;//取根节点
while(1)//找
{
if(!p) return -1;//不存在 (没数)
if(ls(p) && t[ls(p)].siz >= x) p = ls(p);//小于左子树的节点数 在左边
else//在右边
{
x -= ls(p) ? t[ls(p)].siz : 0;//减去左边子树的节点数 到右边找
if(x <= t[p].w) {splay(p); return t[p].v;}//小于这个点的数的数量 找到了 把这个点转到根节点
x -= t[p].w; p = rs(p);//不在这里 继续找
}
}
}
int pre(int x) {//查前驱
insert(rt, 0, x);//插入 这个点会转到根节点
int p = ls(rt);//取左子树的根节点
while(rs(p)) p = rs(p);//在左子树中往右找 直到最后 也就是找到比根节点小的最大值
del(x);//把插入的点删了
return t[p].v;
}
int suc(int x) {//查后继 基本同上
insert(rt, 0, x);
int p = rs(rt);
while(ls(p)) p = ls(p);
del(x);
return t[p].v;
}
}
/*----------------------------------------函数*/
int main() {
n = read();
while(n--)
{
int opt = read(), x = read();
if(opt == 1) Splay::insert(Splay::rt, 0, x);
if(opt == 2) Splay::del(x);
if(opt == 3) printf("%d\n", Splay::rank(x));
if(opt == 4) printf("%d\n", Splay::num(x));
if(opt == 5) printf("%d\n", Splay::pre(x));
if(opt == 6) printf("%d\n", Splay::suc(x));
}
return 0;
}
题目: P3391 【模板】文艺平衡树
关于 \(Splay\) —— 区间树
\(Splay\) 是可以用来维护序列的 这样的 \(Splay\) 就是一棵区间树(有点类似于线段树的亚子) 大概是每个点 就是.. 一个点? 好像...就是一个点
值得注意的是 这里的 \(Splay\) 已经不是一棵二分查找树了 所以并不一定满足二分查找树的性质 维护的时候对于每个点多维护一个 \(size\) 查找一个数的时候不在是按照权值去找(实际上权值在这里已经不是关键值了) 而是按照排名找
我们构建一棵完美的二叉树 对于一个点 它在二叉树中左子树的孩子数加一就是其在原序列中的下标 而由于我们建成的是一棵完美的二叉树 所以不管你怎么转 这一点都是不变的
还需要知道的就是 \(Splay\) 中维护的关键值是原序列对应的下标的值 所以其中序遍历就是原序列 我们进行区间 \([l, r]\) 翻转的操作时 可以先将 \(l - 1\) 对应的节点旋转到根节点 再将 \(r + 1\) 对应的节点旋转到根节点的右子树 这样 这个右子树的左子树就是区间 \([l, r]\) 了 然后我们给这个点打上标记 每次查找时 如果有标记 就将左右子树交换 标记下传就可以了(类似线段树)
\(Splay\)(区间树) 代码实现
关于注释的话 就先 gu 了 后面再补上
/*
Time: 3.17
Worker: Blank_space
Source: P3391 【模板】文艺平衡树
*/
/*--------------------------------------------*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#define Max(x, y) ((x) > (y) ? (x) : (y))
#define Min(x, y) ((x) < (y) ? (x) : (y))
#define Abs(x) ((x) < 0 ? -(x) : (x))
/*--------------------------------------头文件*/
const int A = 1e4 + 7;
const int B = 1e5 + 7;
const int C = 1e6 + 7;
const int D = 1e7 + 7;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
/*------------------------------------常量定义*/
int n, m, cnt, rt;
/*------------------------------------变量定义*/
inline int read() {
int x = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9') {if(ch == '-') f = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') {x = (x << 3) + (x << 1) + (ch ^ 48); ch = getchar();}
return x * f;
}
/*----------------------------------------快读*/
namespace Splay {
#define fa(x) t[x].fa
#define ls(x) t[x].son[0]
#define rs(x) t[x].son[1]
struct node {int fa, son[2], v, siz, w; bool lzy;}t[C];
bool fson(int p) {return rs(fa(p)) == p;}
void push_up(int p) {t[p].siz = t[ls(p)].siz + t[rs(p)].siz + t[p].w;}
void push_down(int p) {
if(!p || !t[p].lzy) return ;
t[ls(p)].lzy ^= 1; t[rs(p)].lzy ^= 1; std::swap(ls(p), rs(p));
t[p].lzy = 0;
}
int add(int fath, int x) {
cnt++; t[cnt].w = t[cnt].siz = 1; t[cnt].fa = fath; t[cnt].v = x;
if(x == 0 || x == n + 1) t[cnt].v = x ? -INF : INF;
return cnt;
}
void rotate(int p) {
int fath = fa(p), gfa = fa(fath), x = fson(p);
t[fath].son[x] = t[p].son[x ^ 1]; fa(t[fath].son[x]) = fath;
t[p].son[x ^ 1] = fath; fa(fath) = p; fa(p) = gfa;
if(gfa) t[gfa].son[t[gfa].son[1] == fath] = p;
push_up(fath); push_up(p);
}
void splay(int p, int tar) {
for(int fath = fa(p); (fath = fa(p)) != tar; rotate(p))
if(fa(fath) != tar) rotate(fson(p) == fson(fath) ? fath : p);
if(!tar) rt = p;
}
int find(int p, int x) {
while(1)
{
push_down(p);
if(x <= t[ls(p)].siz) {p = ls(p); continue;}
if(x == t[ls(p)].siz + 1) return p;
x -= t[ls(p)].siz + 1; p = rs(p);
}
}
void reverse(int l, int r) {
l = find(rt, l); r = find(rt, r); splay(l, 0); splay(r, l);
t[ls(rs(rt))].lzy ^= 1;
}
int build(int fath, int l, int r) {
if(l > r) return 0;
int mid = (l + r) >> 1, p = add(fath, mid);
ls(p) = build(p, l, mid - 1); rs(p) = build(p, mid + 1, r);
push_up(p); return p;
}
void print(int p) {
if(!p) return ; push_down(p);
print(ls(p));
if(t[p].v >= 1 && t[p].v <= n) printf("%d ", t[p].v);
print(rs(p));
}
}
/*----------------------------------------函数*/
int main() {
n = read(); m = read(); rt = Splay::build(0, 0, n + 1);
for(int i = 1; i <= m; i++)
{
int l = read(), r = read();
Splay::reverse(l, r + 2);
}
Splay::print(rt);
return 0;
}
后记:
关于代码的问题
\(Treap\) 的代码主要借鉴的是 \(loceaner\) 的博客
\(Splay\) 的代码主要借鉴的是 \(Luckyblock\) 的博客
所以写法基本相差不是很大 把链接挂在后面


 浙公网安备 33010602011771号
浙公网安备 33010602011771号