实验四

print(sum)
sum = 42
print(sum)

def inc(n):
    sum = n + 1
    print(sum)
    return sum

sum = inc(7) + inc(7)
print(sum)

 

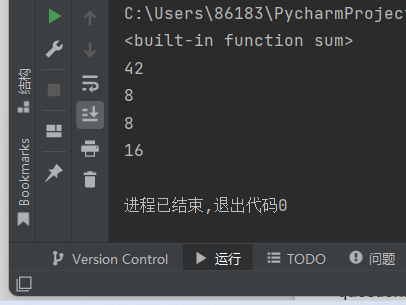
question:task1.py源码中，共有4处有python语句print(sum)（line1, line3, line7, line11)。这4处使用的标识符sum是代表一个变量名吗？如果不是，请分别指出这4行中变量sum的作用域。

answer:不是。

1.Built-in

2.Global

3.Local

4.Global 

task 2_1

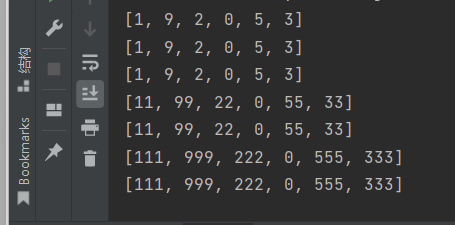
def func1(a,b,c,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的列表
    默认，参数按位置传递；也支持关键词传递
    '''
    return [a,b,c,d,e,f]


def func2(a,b,c,*,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的列表
    *后面的参数只能按关键词传递
    '''
    return [a,b,c,d,e,f]


def func3(a,b,c,/,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的参数
    /前面的参数只能按位置传递
    '''
    return[a,b,c,d,e,f]


print( func1(1,9,2,0,5,3))
print( func1(a = 1,b = 9,c = 2,d = 0,e = 5,f = 3))
print( func1(1,9,2,f = 3,d = 0,e = 5))

print( func2(11,99,22,d = 0,e = 55,f = 33))
print( func2(a = 11,b = 99,c = 22,d = 0,e = 55,f = 33))

print( func3(111,999,222,0,555,333))
print( func3(111,999,222,d = 0,e = 555,f = 333))

 

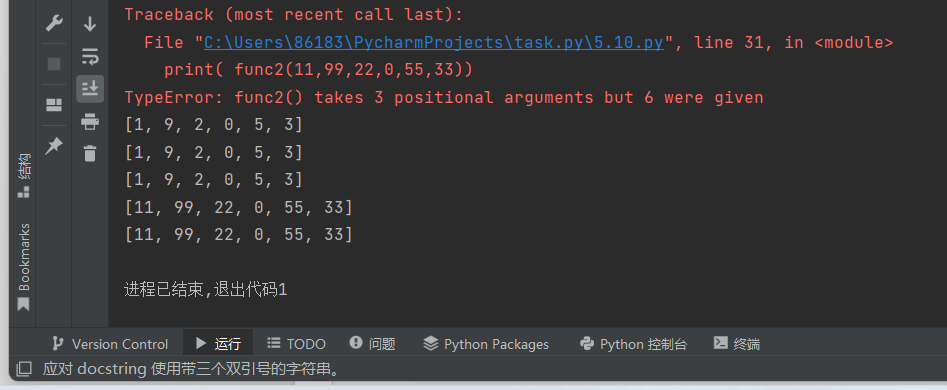
 line30后增加一行函数

def func1(a,b,c,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的列表
    默认，参数按位置传递；也支持关键词传递
    '''
    return [a,b,c,d,e,f]


def func2(a,b,c,*,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的列表
    *后面的参数只能按关键词传递
    '''
    return [a,b,c,d,e,f]


def func3(a,b,c,/,d,e,f):
    '''
    返回参数a,b,c,d,e,f构成的参数
    /前面的参数只能按位置传递
    '''
    return[a,b,c,d,e,f]


print( func1(1,9,2,0,5,3))
print( func1(a = 1,b = 9,c = 2,d = 0,e = 5,f = 3))
print( func1(1,9,2,f = 3,d = 0,e = 5))

print( func2(11,99,22,d = 0,e = 55,f = 33))
print( func2(a = 11,b = 99,c = 22,d = 0,e = 55,f = 33))

print( func3(111,999,222,0,555,333))
print( func3(111,999,222,d = 0,e = 555,f = 333))
print( func3(a = 111,b = 999,c = 222,0,555,333))

 

 

 task2_2

list1 = [1,9,8,4]

print( sorted(list1))
print( sorted(list1,reverse = True))
print( sorted(list1,True))

 

 

 

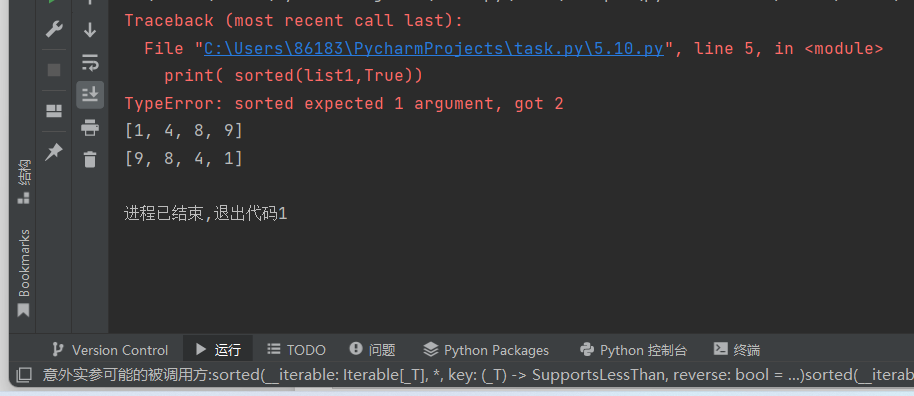
questionr:python内置函数sorted()中，参数reverse的传递方式是否必须使用关键字传递？

answer:是

task2_3

def func(a,b,c,/,*,d,e,f):
    return( [a,b,c,d,e,f] )

print(func(1,2,3,d = 4,e = 5,f = 6))

 

 

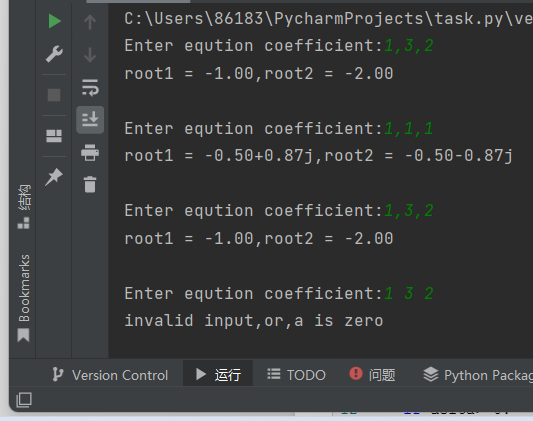
def solve(a,b,c):
    '''
    求解一元二次方程，返回方程的两个根
    :param a,b,c: int 方程系数
    :return: tuple
    '''
    delta = b*b-4*a*c
    delta_sqrt = abs(delta)**0.5
    p1 = -b/2/a
    p2 = delta_sqrt/2/a

    if delta>=0:
        root1 = p1 + p2
        root2 = p1 - p2
    else:
        root1 = complex(p1,p2)
        root2 = complex(p1,-p2)

    return root1,root2


while True:
    try:
        a,b,c = eval(input('Enter eqution coefficient:'))
        if a == 0:
            raise
    except:
        print('invalid input,or,a is zero')
        break
    else:
        root1,root2 = solve(a,b,c)
        print(f'root1 = {root1:.2f},root2 = {root2:.2f}')
        print()

 

 

 

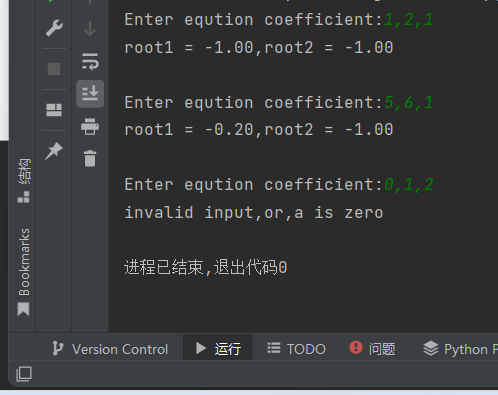
 在line22之前增加一行代码

def solve(a,b,c):
    '''
    求解一元二次方程，返回方程的两个根
    :param a,b,c: int 方程系数
    :return: tuple
    '''
    delta = b*b-4*a*c
    delta_sqrt = abs(delta)**0.5
    p1 = -b/2/a
    p2 = delta_sqrt/2/a

    if delta>=0:
        root1 = p1 + p2
        root2 = p1 - p2
    else:
        root1 = complex(p1,p2)
        root2 = complex(p1,-p2)

    return root1,root2

print(solve.__doc__)
while True:
    try:
        a,b,c = eval(input('Enter eqution coefficient:'))
        if a == 0:
            raise
    except:
        print('invalid input,or,a is zero')
        break
    else:
        root1,root2 = solve(a,b,c)
        print(f'root1 = {root1:.2f},root2 = {root2:.2f}')
        print()

 

 

task4

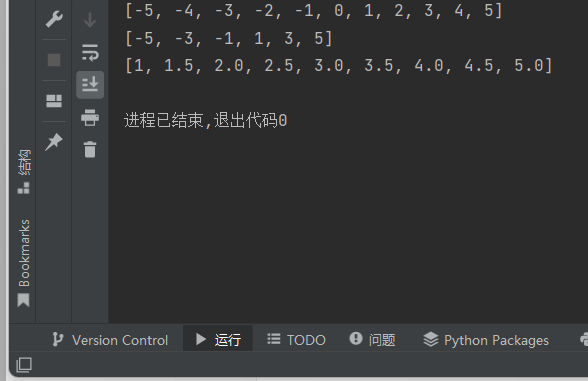
def list_generator(a,b,c = 1):
    y = []
    while a<=b:
        y.append(a)
        a+=c
    return y

list1 = list_generator(-5,5)
print(list1)
list2 = list_generator(-5,5,2)
print(list2)
list3 = list_generator(1,5,0.5)
print(list3)

 

 task5

def is_prime(n):
    x = 2
    m = True
    if n == 2:
        return True
    while n > x:
        if n%x == 0 and m == True:
            m = False
        else:
            x+=1
    return m

for number in range(2,21,2):
    for x in range(2,int(number/2)+1):
        y = number-x
        if is_prime(x) == True and is_prime(y) == True:
            print('{}={}+{}'.format(number,x,y))
            break

 

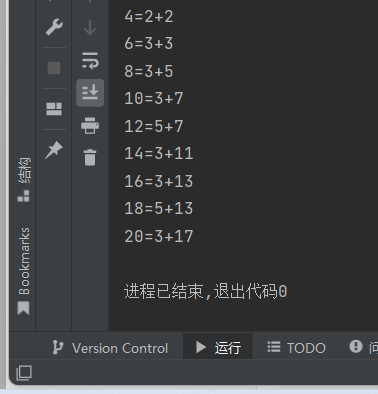
 task6

def encorder(text):
    list = []
    for i in text:
        if 65<=ord(i)<=85 or 97<=ord(i)<=117:
            list.append(chr((ord(i)+5)))
        elif 86<=ord(i)<=90 or 118<=ord(i)<=122:
            list.append(chr(ord(i)-21))
        else:
            list.append(i)
    return ''.join(list)

def decorder(text):
    list = []
    for i in text:
        if 70<=ord(i)<=90 or 102<=ord(i)<=122:
            list.append(chr((ord(i)-5)))
        elif 65<=ord(i)<=69 or 97<=ord(i)<=101:
            list.append(chr((ord(i)+21)))
        else:
            list.append(i)
    return ''.join(list)

text=input('输入英文文本；')
print(f'编码后的文本；{encorder(text)}')
print(f'解码后的文本；{decorder(encorder(text))}')

 

 

 

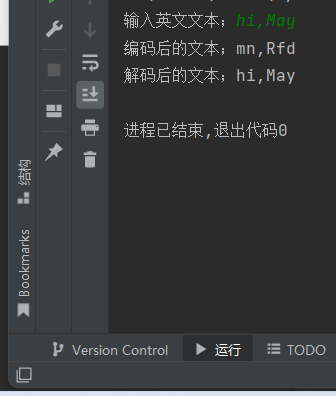
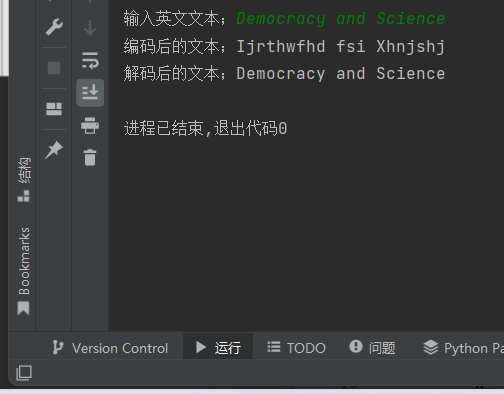
 task7

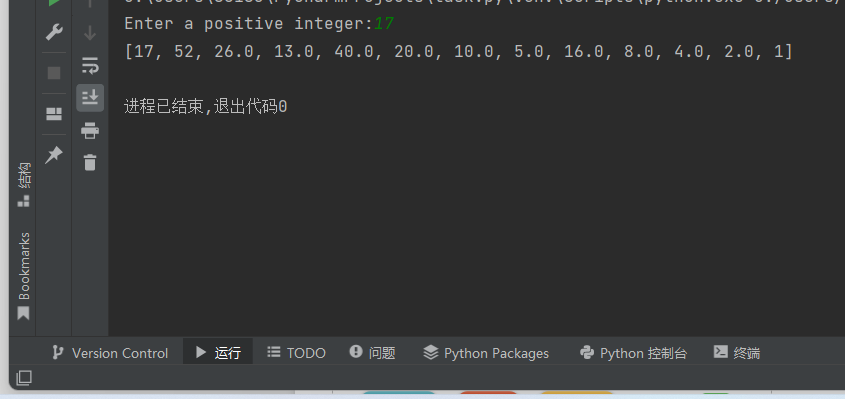
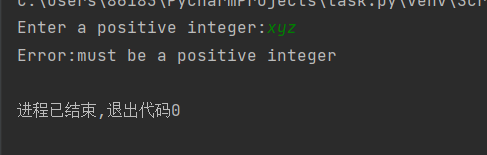
def collatz(n):
    if n%2 == 0:
        return n/2
    else:
        return 3*n+1

try:
    n =int(input('Enter a positive integer:'))
    if n > 0:
        list = []
        while n != 1:
            list.append(n)
            n = collatz(n)
        list.append(1)
        print(list)
    else:
        print('Error:must be a positive integer')
except:
    print('Error:must be a positive integer')

 

 

 

 

 

 

 

 

 

 

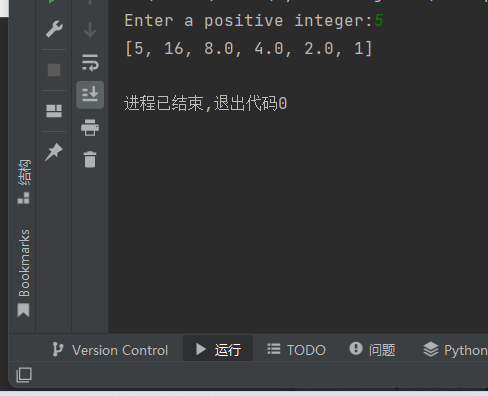
实验总结：

1.对于try...except...的使用仍不熟练，需要加强练习

2.对于chr(),ord()的使用仍不熟练，需要加强练习

3.对于函数的编写能力有了一定的提升，希望自己能够继续努力