C / C++ Data Structure
- 用低劣的水平描述数据结构的东西,后续考研还要细学
- 目前主要加深对数据结构的理解,大体过一遍,如果你质疑我的文章,那一定是我错了,我会忽略一些专业术语,更偏向于自己的理解思考
- 对于初学者来说可能会有一定的帮助
前置
- 一堆概念
- 数据:客观事物的符号描述
- 数据元素:数据的基本单位
- 数据项:组成数据元素的、有独立含义的、不可分割的最小单位
- 数据对象:性质相同的数据元素的集合
- 逻辑结构
- 线性与非线性
- 线性、树、图、集合
- 存储结构
- 散列与性能分析
为什么学习数据结构?
- 学习数据结构和算法,并非为了死记硬背几个知识点。而是为建立时间复杂度、空间复杂度意识,写出高质量代码,能够设计基础架构,提升编程技能,训练逻辑思维,积攒人生经验,以此获得工作回报,实现你的价值,完善你的人生。 掌握数据结构与算法,看待问题的深度,解决问题的角度就会完全不同。
线性表
顺序表
前哨
输入特殊值后,表示输入结束的特殊值为前哨。
typedef
语句格式
typedef 实存类型 类型别名
一系列操作
定义的结构体
typedef struct
{
Type* data;
int max;
int size;
}Seqlist
尾插
插入前判断一下是否需要扩展空间,需要的话执行
void Reserve(Seqlist * l,int newmax)
{
int i ;
Type * old;
if(newmax <= l->max)
return ;
old = l -> data;
l -> max = newmax;
l -> data = (Type *) malloc (newmax * sizeof(Type));
for(int i = 0 ; i < l -> size ; i ++)
l -> data[i] = l -> old[i];
free (old);
}
尾插操作
void PushBack(Seqlist * l ,Type item)
{
if(l -> size == l -> max)
Reserve(l,2*max);
l -> data[l -> size ] = item;
l -> size++;
}
进行读取操作时,指针前面加const可以确保不会修改数据
删除
void Erase(Seqlist * l , int id)//删除第id元素
{
int i ;
for(i = id +1 ; i < l -> size ; i ++)
l -> data[i-1] = l -> data[i];
l ->size --;
}
定点插入
void intsert(Seqlist* l ,int id , Type item)
{
int i;
if(l -> size == l -> max)
Reserve(l,2*l -> max);
for(i = l -> size-1 ; i >= id ; i --)
l -> data[i+1] = l -> data[i];
l -> data[id] = item;
l -> size ++;
}
链表
单链表
循环链表
双向链表
链表逆置
将第二个结点及以后节点进行遍历,执行先首插再删除的操作,直到next==last
栈和队列
栈(先进先出)
- 没什么说的
前缀、中缀和后缀表达式
1. 中缀表达式 (需要界限符)
运算符在两个操作数中间:
① a + b
② a + b - c
③ a + b - c*d
④ ((15 ÷ (7-(1+1)))×3)-(2+(1+1))
⑤ A + B × (C - D) - E ÷ F
2. 后缀表达式 (逆波兰表达式)
运算符在两个操作数后面:

中缀表达式转后缀表达式-手算
-
步骤1: 确定中缀表达式中各个运算符的运算顺序
-
步骤2: 选择下一个运算符,按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数
-
步骤3: 如果还有运算符没被处理,继续步骤2
“左优先”原则: 只要左边的运算符能先计算,就优先算左边的 (保证运算顺序唯一);
中缀:A + B - C * D / E + F
后缀:A B + C D * E / - F +
重点:中缀表达式转后缀表达式-机算
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
- 遇到操作数: 直接加入后缀表达式。
- 遇到界限符: 遇到 ‘(’ 直接入栈; 遇到 ‘)’ 则依次弹出栈内运算符并加入后缀表达式,直到弹出 ‘(’ 为止。注意: '(' 不加入后缀表达式。
- 遇到运算符: 依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到 ‘(’ 或栈空则停止。之后再把当前运算符入栈。
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
后缀表达式的计算—手算:
从左往右扫描,每遇到一个运算符,就让运算符前面最近的两个操作数执行对应的运算,合体为一个操作数;
注意: 两个操作数的左右顺序
重点:后缀表达式的计算—机算
用栈实现后缀表达式的计算(栈用来存放当前暂时不能确定运算次序的操作数)
-
步骤1: 从左往后扫描下一个元素,直到处理完所有元素;
-
步骤2: 若扫描到操作数,则压入栈,并回到步骤1;否则执行步骤3;
-
步骤3: 若扫描到运算符,则弹出两个栈顶元素,执行相应的运算,运算结果压回栈顶,回到步骤1;
注意: 先出栈的是“右操作数”
3.前缀表达式 (波兰表达式)
运算符在两个操作数前面:
(3+4)×5-6 对应的前缀表达式是: - × + 3 4 5 6
前缀表达式的计算机求值过程
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果。
4.中缀表达式的计算(用栈实现)
两个算法的结合: 中缀转后缀 + 后缀表达式的求值
初始化两个栈,操作数栈 和运算符栈
若扫描到操作数,压人操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈 (期间也会弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈项元素并执行相应运算,运算结果再压回操作数栈)
队列
- 普通队列 queue
- 循环队列
- 双向队列 deque
- 优先队列 priority_queue
KMP字符串匹配
- 根据模式串t,求出next数组(只与模式串有关,与主串无关),利用next数组进行匹配,当匹配失败时,主串的指针 i 不再回溯!
- 所谓next,就是每个字符的最长相同前后缀,代码上注意递归求解即可
结构体设置
#define MAXSIZE 1024
typedef struct{
char ch[MAXSIZE+1]; //字符串
int length; //长度
}String;
求解next数组
void Get_Next(String t, int nextval[])
{
nextval[0] = -1;
int i = 0, j = -1;
while(i < t.length){
//相同前后缀,进入判断
if(j == -1 || t.ch[i] == t.ch[j]){
i++, j++; //修改位置
if(t.ch[i] != t.ch[j])
nextval[i] = j; //不相等,直接取值
else
nextval[i] = nextval[j]; //相等,无意义,再次向前求解
}else
j = nextval[j]; //非相同前后缀,向前递归
}
}
KMP
int KMP(String s, String t)
{
int nextval[MAXSIZE+1];
Get_Next(t, nextval); //求解nextval
int i = 0, j = 0;
while(i < s.length && j < t.length){
if(j == - 1 || s.ch[i] == t.ch[j]){ //相同,可匹配
i++, j++;
}else //不可匹配,向前追溯
j = nextval[j];
}
//输出匹配位置
if(j >= t.length)
return i - t.length + 1; //输出实际位置长度,非数组下标
return 0;
}
树
一堆概念
- 结点
- 父母结点、祖先结点、左右孩子结点、兄弟结点、子孙结点、前后辈结点
- 结点的度、结点的层次、树的高度
- 有序树、无序树
- 二叉树 、 完全二叉树 、满二叉树 、线索二叉树
二叉树的存储
顺序存储
- 自上而下,从左到右
- 二叉树中没有的结点用0表示放进一维容器
- 若某一结点下标为p,则左儿子为2p,右儿子为2p+1
链式存储
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
一般来说,和树有关系的操作大多能用递归解决
二叉树的遍历
前序遍历
先序遍历可以想象为,一个小人从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果
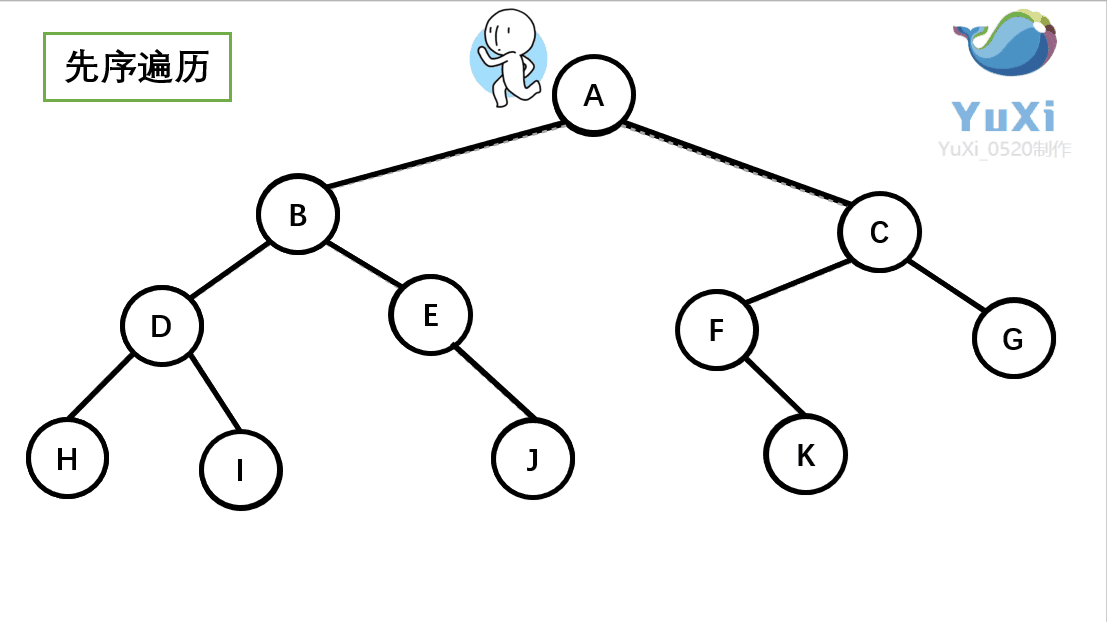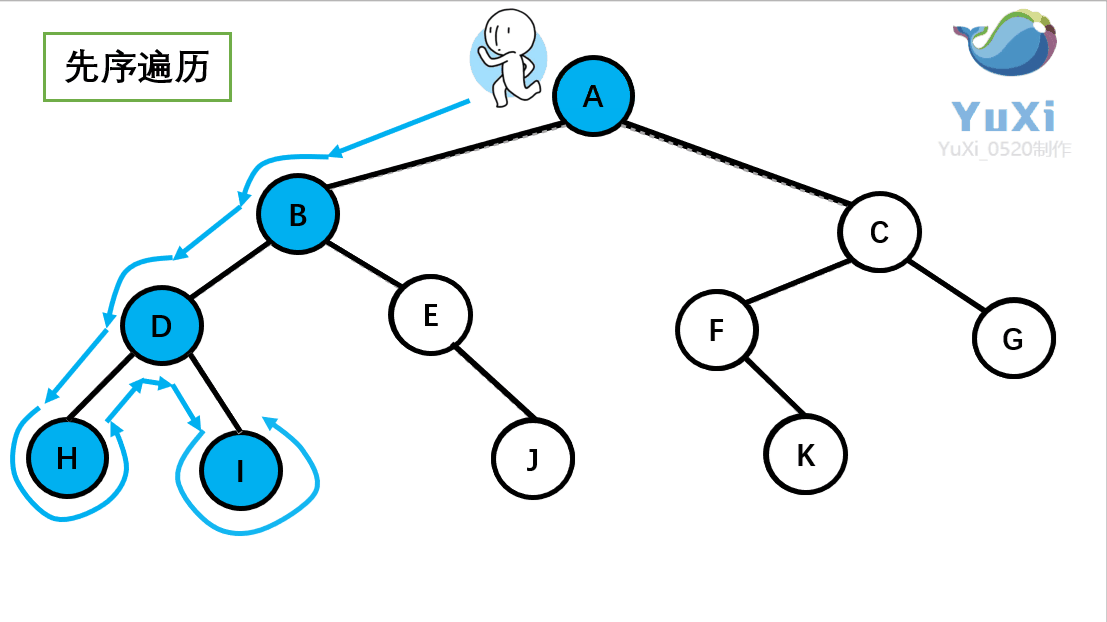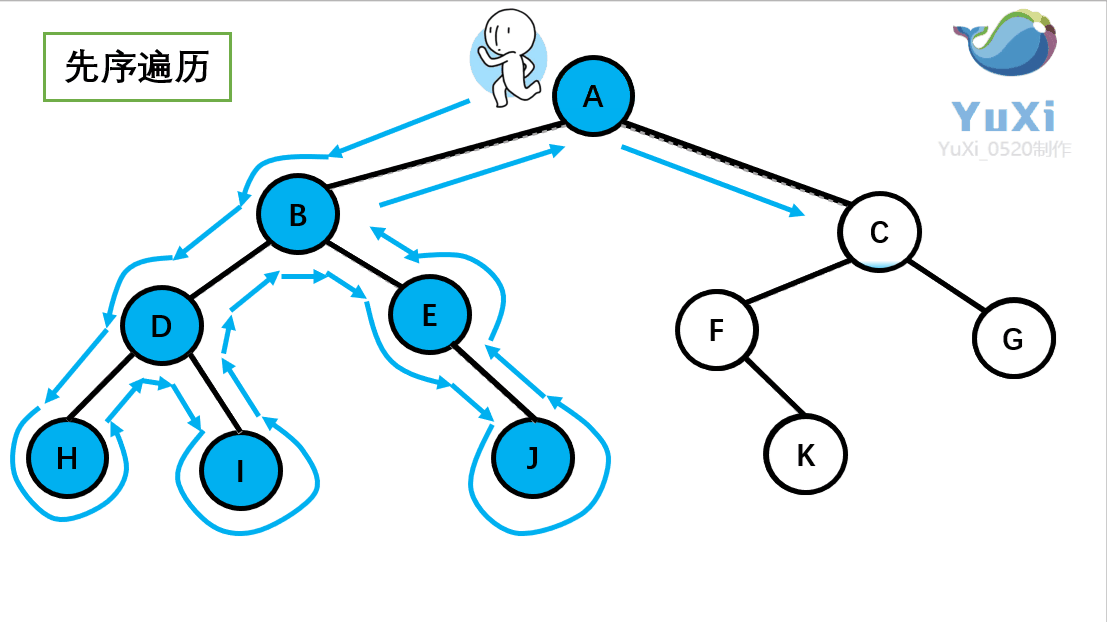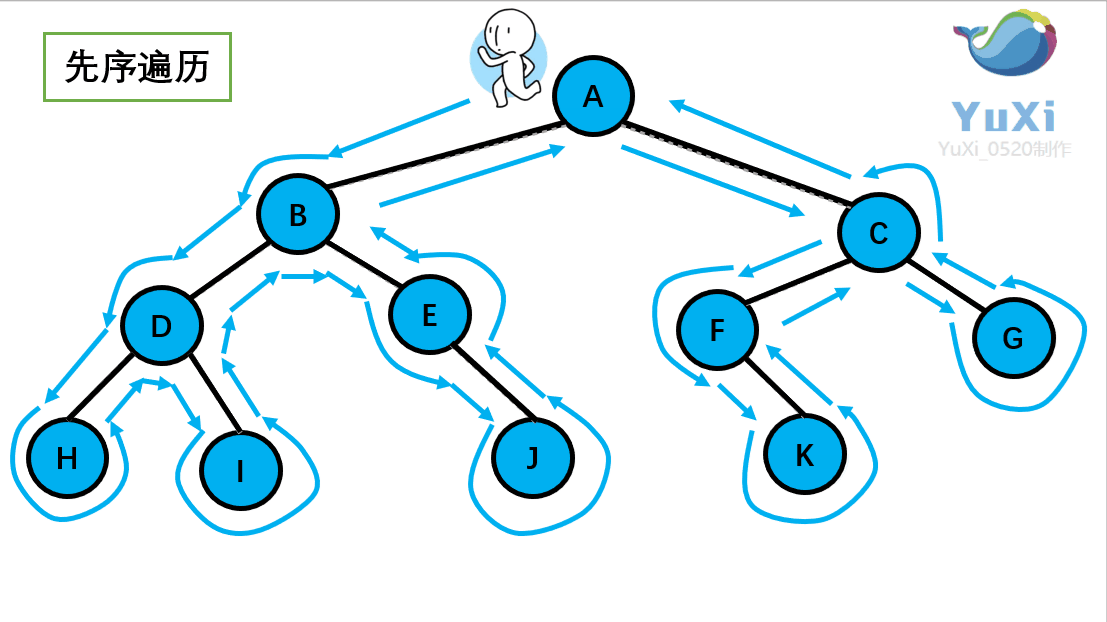
先序遍历结果为:A B D H I E J C F K G
代码:
void front(TreeNode x){
cout <<x->val <<" "; //输出根
front(x->left); //递归左儿子
front(x->right); //递归右儿子
}
中序遍历
中序遍历可以看成,二叉树每个节点,垂直方向投影下来(可以理解为每个节点从最左边开始垂直掉到地上),然后从左往右数,得出的结果便是中序遍历的结果
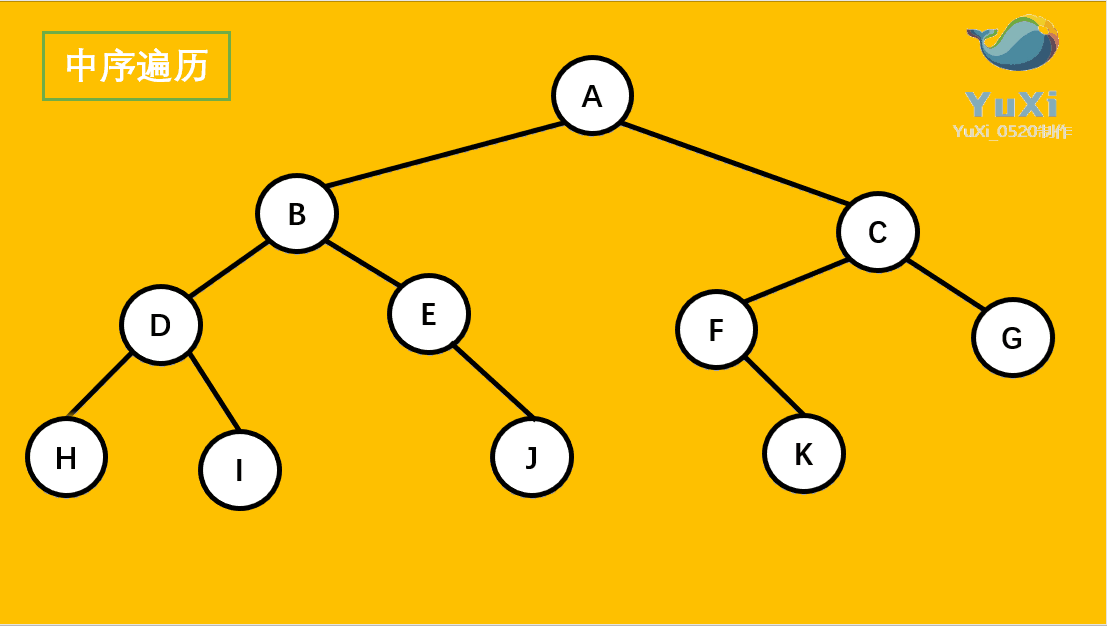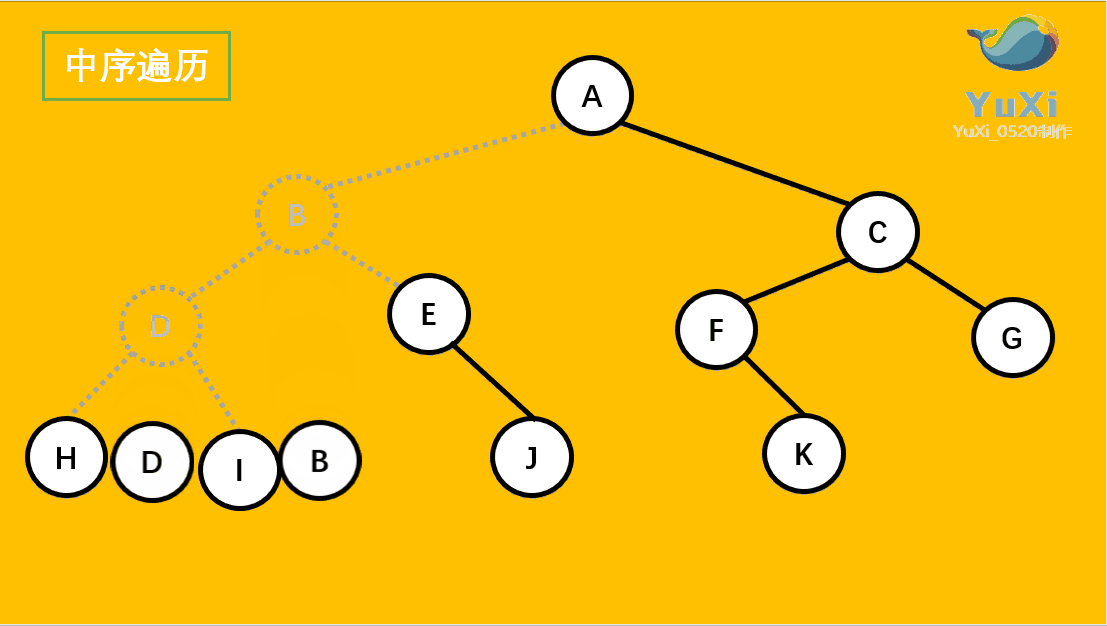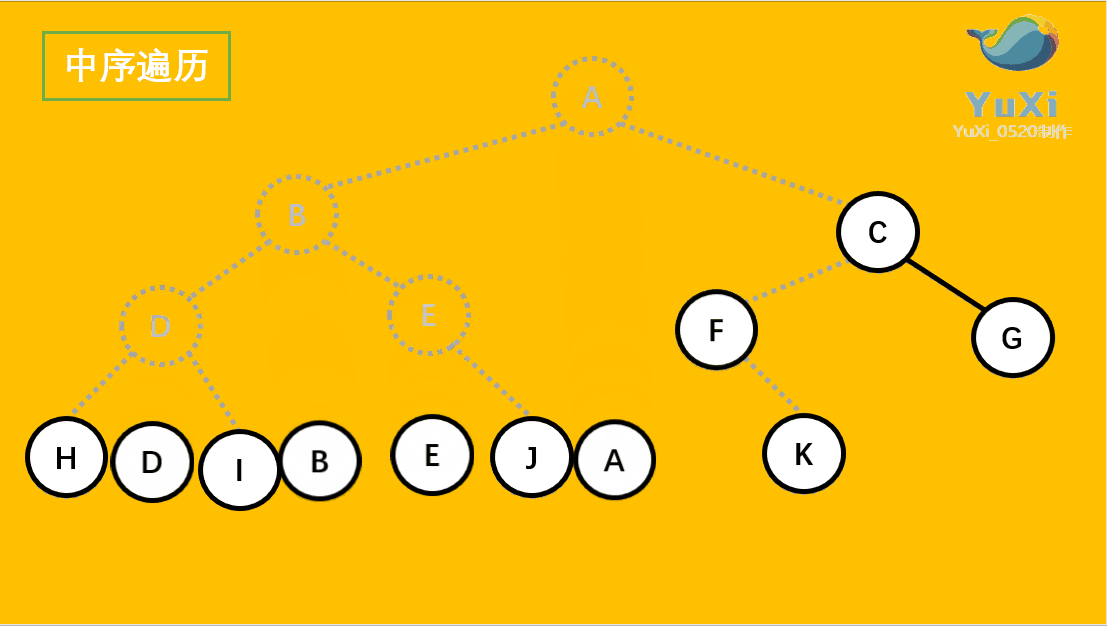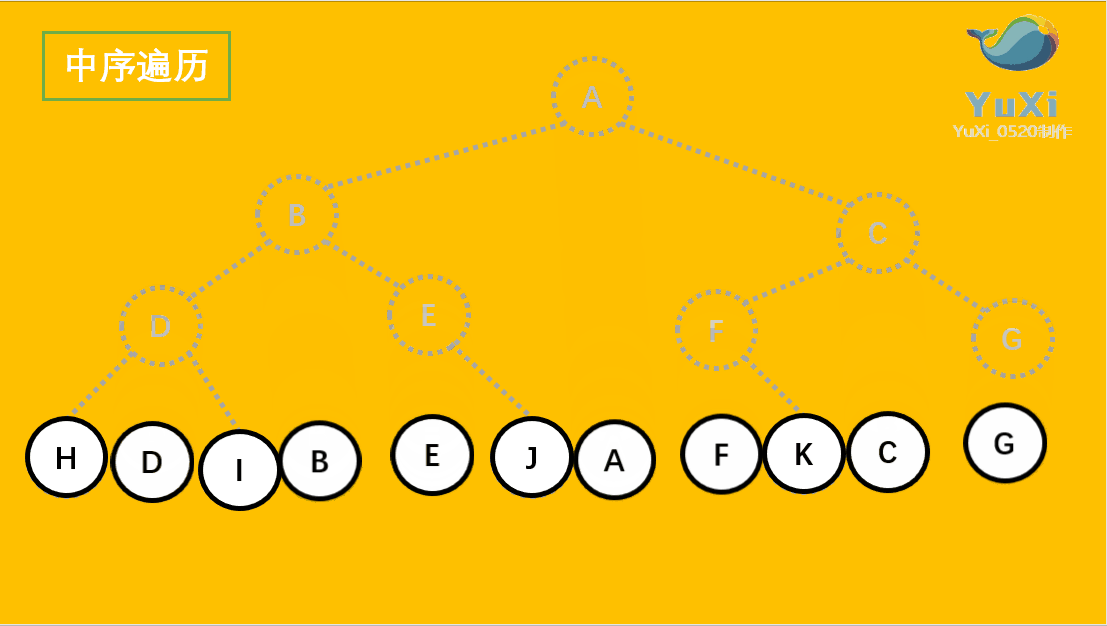
中序遍历结果:H D I B E J A F K C G
后序遍历
后序遍历可以理解为:从左到右,从下往上数得出的结果就是后序遍历的结果
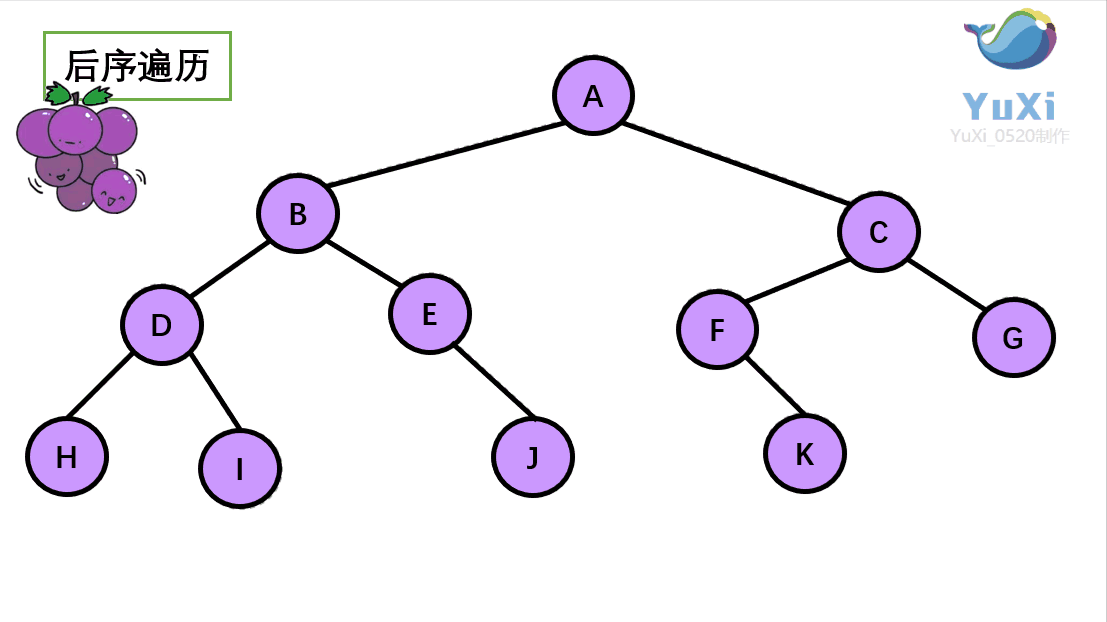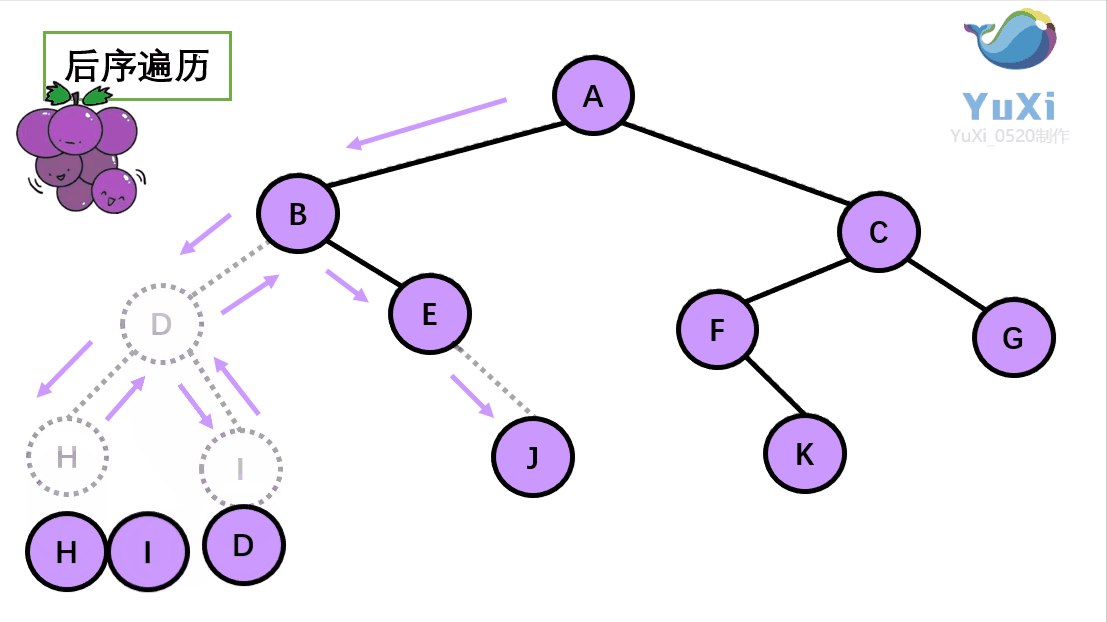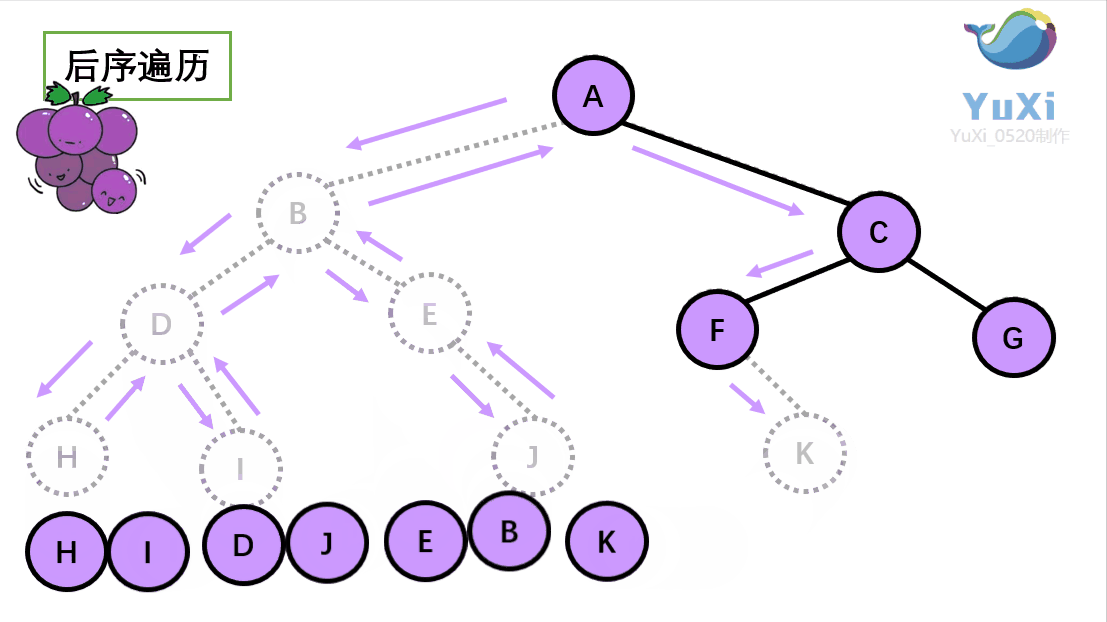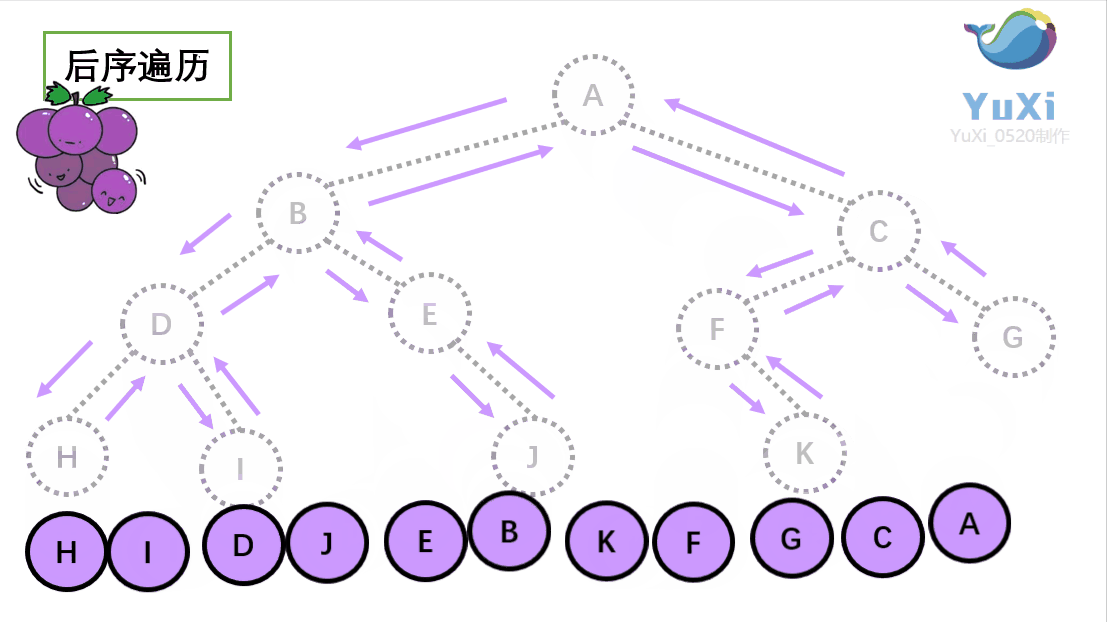
后序遍历结果:H I D J E B K F G C A
层序遍历
从根节点开始,从左往右一层一层输出即可
树的遍历
没有中序遍历,其他三种都有
森林
- 森林是m棵互不相交的树的集合。对树中的每个结点而言,其子树的集合即为森林。删去一棵树的根,就得到一个森林。
二叉树、树、森林的转换(左孩子右兄弟)
- 树变二叉树
- 在所有的兄弟之间连线
- 只保留父节点与第一个儿子结点的连线,去掉其他父子结点之间的连线
- 森林变二叉树
- 将各棵树分别转换成二叉树。
- 将将每棵树的根结点用线相连。
- 以第一棵树的根结点为二叉树的根,再以根结点为轴心,顺时针旋转,形成二叉树型结。
- 二叉树变森林
- 对于一个结点x,他是父结点的左孩子,在父节点和结点x的右孩子、以及其右孩子的右孩子…之间连线
- 去掉所有结点与右孩子的连线(刚刚连的线不是此连线故不会被去掉)
二叉排序树
- 中序遍历后可以得到有序的序列
- 左子树结点值<跟结点值<右子树结点值
二叉树的增删结点
#include <iostream>
#define INF 1e8
using namespace std;
struct TreeNode{
int val;
TreeNode * left,* right;
TreeNode(int _val): val(_val),left(NULL),right(NULL){}
}*root;
void insert(TreeNode * &root , int n) //插入结点
{
if(!root) root = new TreeNode (n);
else if(n > root -> val ) insert(root -> right, n);
else insert(root -> left,n);
}
void remove(TreeNode* &root,int n) //删除结点
{
if(!root) return;
if(n > root -> val) remove (root -> right,n);
else if (n < root -> val) remove (root -> left,n);
else{
if(!root -> left && !root -> right) root = NULL;
else if(!root -> left) root = root ->right;
else if(!root -> right) root = root -> left;
else{
auto p = root -> left;
while(p -> right) p = p -> right;
root -> val = p -> val;
remove(root -> left,p -> val);
}
}
}
int get_front(TreeNode *root,int n) //获得前驱结点值
{
if(!root) return -INF;
if(n <= root -> val) return get_front(root ->left,n );
else return max(root -> val , get_front(root -> right,n));
}
int get_behind(TreeNode *root,int n) //获得后继结点值
{
if(!root) return INF;
if(n >= root -> val) return get_behind(root ->right,n );
else return min(root -> val , get_behind(root -> left,n));
}
int main()
{
int n;
cin >> n;
while(n--)
{
int t,x;
cin >> t >> x;
if(t == 1) insert(root,x);
else if(t == 2) remove(root,x);
else if(t == 3) cout << get_front(root,x)<<endl;
else cout << get_behind(root,x)<<endl;
}
return 0;
在删除结点时,该点是:
- 叶子结点,直接删除
- 只有左子树或者只有右子树的结点,将子树提上去
- 若左右子树都在的结点,将该节点前驱的值赋值给该结点,删掉其前驱
平衡树(AVL)
定义:
- a. 是二叉查找树
- b. 每个节点的左子树和右子树的高度差最多为1
平衡因子:
一个结点的左子树的高度减去右子树的高度,可取-1、0、1三种值
平衡操作
- 1.找到最小不平衡子树
- 2.找到中心结点往上“提”
哈夫曼树
哈夫曼树(一般是二叉树,m叉也可)
- 最优树,带权路径最短,也就是所有结点的深度与权值积之和最小
哈夫曼编码
- 在哈夫曼树上按照左0右1的规则从根节点走到目标节点形成的数字串
哈夫曼树的构造
-
将所有叶节点按照权值从小到大排序,作为初始的n棵二叉树,其中n为叶节点的个数。
-
从n棵二叉树中选取权值最小的两棵二叉树合并成一棵二叉树,新的二叉树的根节点权值为这两棵二叉树的权值之和。
-
将新生成的二叉树插入到原来的n棵二叉树中,并将这两棵二叉树从n棵二叉树中删除。
-
重复步骤2和3,直到n棵二叉树合并成一棵哈夫曼树。
图
前置概念
- 有向图、无向图、混合图
- 点、权值
- 出度、入度
- 边、弧
- 强连通(有向图)
- 两个顶点强连通:两个顶点至少存在一条互相可达路径
- 强连通图:任意两个顶点强连通
- 强连通分量:非强连通图中的最大强连通子图
- 连通、回路(环)、稀疏图、稠密图
- 零图:仅有孤立结点
- 平凡图:只有一个孤立结点
- 多重图:有多重边的图。非多重图为线图
- 简单图:无多重边和自回环的图
- 完全图:任意两个不同结点之间都有边的简单图
- 无向完全图的边数为n(n-1)/2
- 有向完全图的边数为n(n-1)
- k度正则图:在无向图G=<V,E>中,每个结点的度都是k
- 点割集:有一个连通图和点的集合,如果在图上把所有集合中的点删去,这个图就不是连通图,而这个集合中的点少一个,它还是连通图,这个集合就叫点割集
- 割点:存在两个点u、w,使得uw之间的每一条通路都必须经过点v,那么v就是割点。意思也就是没了v他就不是个连通图
- 结点连通度:在一个非完全图的连通图里,变为不连通图所需删去结点的最小数目
- 边割集、割边、边连通度
- 结点连通度𝜅(G) ≤ 边连通度𝜆(G) ≤ 最小度δ(G)
图的存储
邻接矩阵
- map[a,b] = c
- 表示有向图 a -> b 有一条边,无向图就相当于俩条有向边合并
- c表示存在边或者路径权值
邻接表(类似于树的孩子链表示法)
- 类似于二维向量
- 把每个点摘出来是一维
- 对于每个点,把每个与他相关的点都存一遍是二维
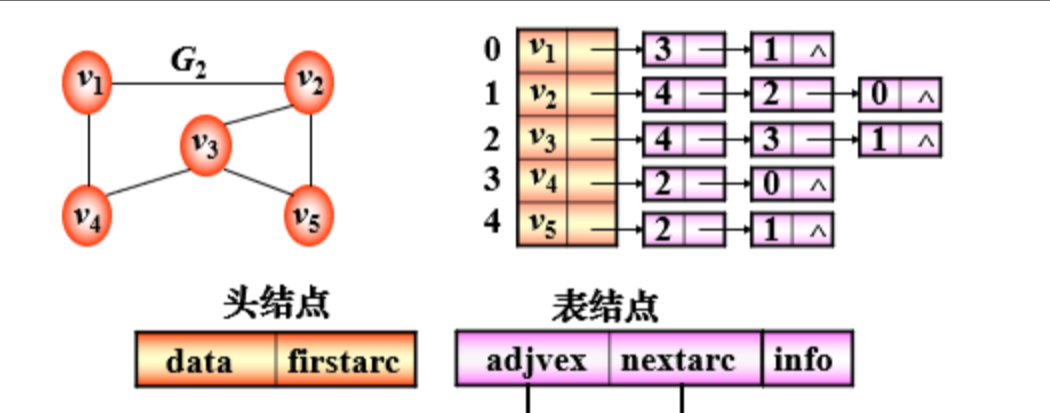
逆邻接表
都是存储下标
| 邻接表 | 逆邻接表 | |
|---|---|---|
| 特点 | 链表结点 ↔ 出度 顶点Vi的出度为第i个单链表中结点的个数 顶点Vi的入度为整个链表中邻接点域值为i-1的个数 |
链表结点 ↔ 出度 顶点Vi的入度为第i个单链表中结点的个数 顶点Vi的出度为整个链表中邻接点域值为i-1的个数 |
邻接点不包含头结点
十字链表(有向图)
可以说它是邻接表+逆邻接表
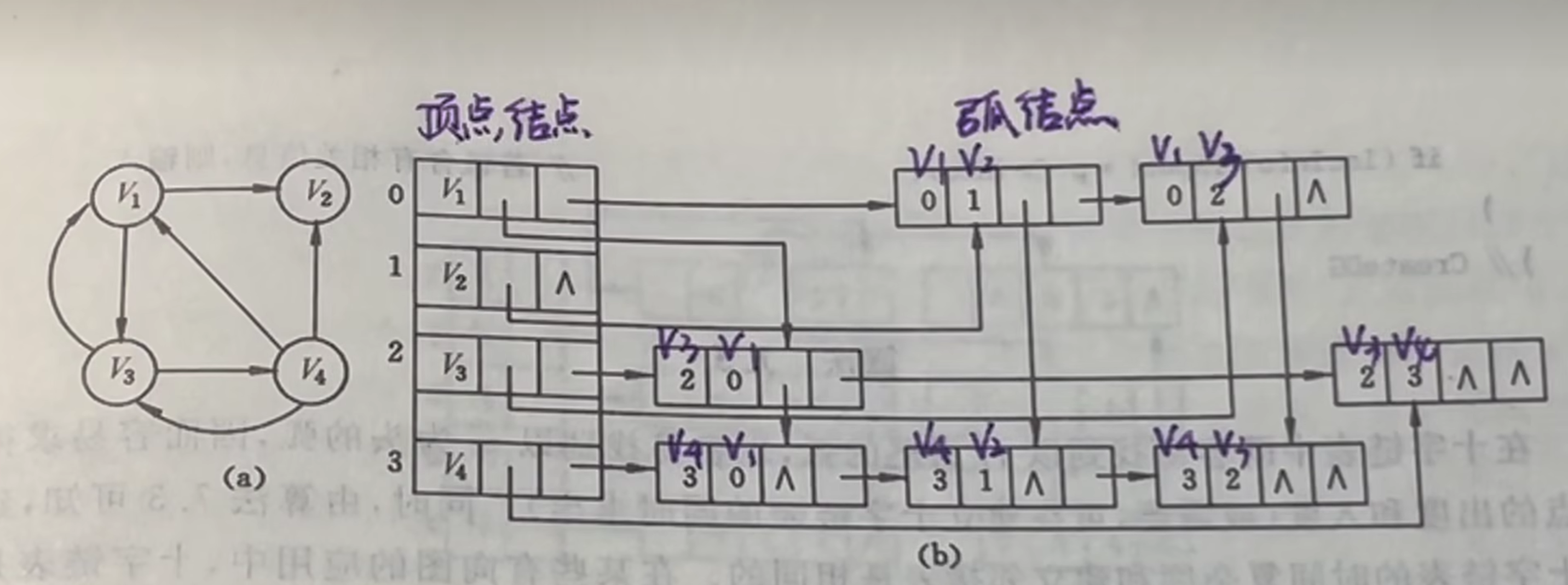
//这玩意只是为了更加形象,不代表就这么简单
struct Node{
int u; //弧尾
int v; //弧头
int value; //权值
struct Node *hlink; //指向下一个弧头相同的Node结构(逆邻接表)
struct Node *tlink; //指向下一个弧尾相同的Node结构(邻接表)
}
邻接多重表(无向图)
和十字链表的区别在于弧变成了边
struct Node{
int u; //边的一个结点
int v; //边的另一个结点
int value; //权值
struct Node *hlink; //指向下一个含u的Node结构
struct Node *tlink; //指向下一个含v的Node结构
}
| 数据结构 | 空间复杂度 | 适用范围 | 缺点 |
|---|---|---|---|
| 邻接表 | 有向图o(V+2E),无向图o(V+E) | 稀疏图 | 查找边的时间复杂度较高 O(V) |
| 邻接矩阵 | O(V^2) | 稠密图 | 占用大量空间可能导致内存不足 |
| 十字链表 | O(V + E) | 有向图 | 查找边的时间复杂度较高 O(V) |
| 邻接多重表 | O(V + E) | 无向图 | 查找边的时间复杂度较高 O(V) |
查边时间复杂度高说明点和边难删除,一找就需要遍历。邻接矩阵删除点的时候相关的行和列都要删除
搜索
深度优先遍历
- 不撞南墙不回头
广度优先遍历
- 同深度的路同时试探,多点开花
拓扑排序
- 有向无环图
具体步骤
- 找一个无前驱(入度为0)的点存入拓扑序,或者找到后直接输出
- 将该点以及所有以该点作为起点的边删掉
- 重复1、2操作,直到所有的点都存入拓扑序中或者找不到入度为0的点
注意
1.能检测图中是否带环。由步骤就可以看出带环的图无法进行拓扑排序
2.同一个图拓扑排序结果可能不同。因为可能存在许多个入度为0的点,此时就可以选择不同的点继续进行拓扑排序,所以拓扑排序的解不是唯一的
应用范围
- 检测一个图是否含有环
- 求解AOE图的关键路径
- 在有承接关系的工程中计算最优的项目处理顺序
代码实现
#define N 1000
vector<vector<int>> p(N,vector<int>(N, -1)); //vector变长数组来写邻接矩阵
queue<int> q; //队列操作
int d[N]; //统计入度
int cnt,ans[N]; //cnt记录排序后点的数量,ans数组记录排序结果
bool Topo_sort(){
//存度
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
//指向边不存在或者指向自己
if(i == j || p[i][j] == -1) continue;
d[j]++;
}
}
for(int i = 1;i <= n; i++)
{
if(!d[i]) q.push(i); //统计最初入度,找入度为0的点
}
while(q.size())
{
int t = q.front();q.pop();
ans[cnt++] = t;
for(int i = 1;i <= n; i++)
{
if(p[t][i]!=-1) {
d[i]--; //删边操作
if(d[i] == 0) q.push(i); //如果删完边后入度为0了,放入队列 }
}
}
//得到的拓扑序中的点的个数小于图中点的个数
//说明拓扑排序无法完成,可能存在自环
if(cnt != n ) return false;
else return true;
最小生成树-prim
1.将图分成两个部分,在树里的部分和不在树里的部分
2.选择一条权值最小的边,且该边所连的两个点一个在树内,一个在树外
3.将选定的边加入树内,并将该边的权值记录
4.重复上述操作直到所有的点都被加入树中
#include <bits/stdc++.h>
using namesapce std;
const int M = 50000;
const int N = 10000;
int n, m, res = 0;
//链式前向星建图
struct Node{
int x, v, next;
}edge[M*2+1];
int head[N+1], cnt = 0, dis[N+1];
void addedge(int x, int y, int z){
edge[++cnt].x = y;
edge[cnt].v = z;
edge[cnt].next = head[x];
head[x] = cnt;
}
//边权优先队列
struct ty{
int x, len;
//重载小于号
bool operator < (const ty &a) const{
return len > a.len;
}
}temp;
priority_queue<ty>q;
bool vis[N+1];
void prim()
{
//以初始点1更新队列
vis[1] = true;
for(int i = head[1]; i != -1; i = edge[i].next){
temp.x = edge[i].x;
dis[edge[i].x] = edge[i].v;
temp.len = edge[i].v;
q.push(temp);
}
while(!q.empty()){
//将当前边权最小的可连接点加入树中
//并更新最小生成树代价
ty tmp = q.top(); q.pop();
if(vis[tmp.x]) continue;
vis[tmp.x] = true;
res += tmp.len;
//将新加入点所连接的边放进队列
for(int i = head[tmp.x]; i != -1; i = edge[i].next){
if(vis[edge[i].x]) continue;
//大于等于之前所选边权的新边权无需放入
if(dis[edge[i].x] <= edge[i].v) continue;
//
tmp.x = edge[i].x;
dis[edge[i].x] = edge[i].v;
tmp.len = edge[i].v;
q.push(tmp);
}
}
//输出
cout <<res;
}
int main(void)
{
memset(head, -1, sizeof(head));
memset(dis, 0x3f, sizeof(dis));
memset(vis, false, sizeof(vis));
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
int a, b, v;
scanf("%d%d%d", &a, &b, &v);
addedge(a, b, v);
addedge(b, a, v);
}
prim();
return 0;
}
最小生成树-kruskal
- 将所有的边按大小进行排序
- 选择一条之前未选择过的且权值最小的边
- 利用并查集判断选出的边所连接的两个点当前是否在一个集合里,如果不在,就将该边计入,并更新并查集信息
- 重复2、3操作直到所有的点生成一颗树
#include <bits/stdc++.h>
using namesapce std;
const int M = 50000;
const int N = 10000;
int n, m, res = 0;
//边结构体
struct Node{
int x, y, v;
}edge[M+1];
//按边权值升序排列
bool cmp(Node a, Node b){
return a.v < b.v;
}
//并查集查找父节点以及路径压缩
int fa[N+1];
int find(int x){
if(fa[x] == x)
return x;
else
return fa[x] = find(fa[x]);
}
void Kruskal()
{
//初始化并查集
for(int i = 1; i <= n; i++) fa[i] = i;
//按边权排序
sort(edge+1, edge+1+m, cmp);
//依次拿边
for(int i = 1; i <= m; i++){
//判断选定边所连的两个点是否已经在树里
int fx = find(edge[i].x);
int fy = find(edge[i].y);
if(fx == fy) continue;
res += edge[i].v;
fa[fx] = fy;
}
cout <<res;
}
int main(void)
{
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
int a, b, v;
scanf("%d%d%d", &edge[i].x, &edge[i].y, &edge[i].v);
}
Kruskal();
return 0;
}
最短路
- 单源最短路: 求一个点到其他点的最短路
- 多源最短路: 求任意两个点的最短路
稠密图用邻接矩阵存,稀疏图用邻接表存储。
- 稠密图: m 和 n2 一个级别
- 稀疏图: m 和 n 一个级别
dijkstra算法
描述:首先找到一个没有确定最短路且距离起点最近的点,并通过这个点将其他点的最短距离进行更新。每做一次这个步骤,都能确定一个点的最短路,所以需要重复此步骤 n 次,找出 n 个点的最短路。
核心代码:
const int N = 510;
int n,m;
int g[N][N]; // 邻接矩阵
int dist[N]; // 第 i 个点到起点的最短距离
bool st[N]; // 代表第 i 个点的最短路是否确定、是否需要更新
void dijkstra(){
for(int i=0; i<n; i++)
{
int t = -1;
for(int j=1; j<=n; j++) // 在没有确定最短路中的所有点找出距离最短的那个点 t
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t=j;
st[t]=true; // 代表 t 这个点已经确定最短路了
for(int j=1; j<=n; j++) // 用 t 更新其他点的最短距离
dist[j] = min(dist[j],dist[t]+g[t][j]);
}
}
堆优化版
typedef pair<int,int> PII; //first存距离,second存结点编号
const int N = 2e5+10;
int n,m;
int h[N],w[N],e[N],ne[N],idx; // 邻接表的存储
int dist[N]; // 第 i 个点到起点的最短距离
bool st[N]; // 代表第 i 个点的最短路是否确定、是否需要更新
int dijkstra()
{
memset(dist,0x3f,sizeof(dist)); // 将所有距离初始化正无穷
dist[1] = 0; // 第一个点到起点的距离为 0
priority_queue<PII, vector<PII>, greater<PII>> heap; // 小根堆
heap.push({0,1}); //把 1 号点放入堆中
while(heap.size()) // 堆不空
{
PII t = heap.top(); //找到当前距离最小的点
heap.pop();
int ver = t.second,distance = t.first; // ver为编号,distance为距离
if(st[ver]) continue; // 重边的话不用更新其他点了
st[ver] = true; //标记 t 已经确定最短路
for(int i = h[ver]; i!=-1; i=ne[i]) // 用 t 更新其他点的最短距离
{
int j = e[i];
if(dist[j] > distance + w[i])
{
dist[j] = distance + w[i];
heap.push({dist[j],j}); //入堆
}
}
}
if(dist[n] == 0x3f3f3f3f) return -1; // 说明 1 和 n 是不连通的,不存在最短路
return dist[n];
}
以上使用数组模拟邻接表,结构体更佳
floyed算法
算法简洁描述:
通过不断选取中间点来更新从点 i 到点 j 的最短路径
更新方式:
将现有的点 i 到 j 的最短距离 与 已知点 i 到中间点 k 的最小距离 + k 到 j 的路径距离 进行比较
基本实现
目标
读入有向图进行多源最短路计算
代码
#include<iostream>
#include<calgorithm>
using namespace std;
const int N = 210;
int dist[N][N];
int n,m;
void Floyed()
{
for(int k = 1; k <= n; k++){ //中间点
for(int i = 1; i <= n; i++){ //起始点
if(i == k) continue;
for(int j = 1; j <= n; j++){ //末尾点
if(i == j) continue;
dis[i][j] = min(dis[i][j], dis[i][k] + G[k][j]);
}
}
}
}
int main(){
cin >> n >> m ;
memset(dist,0x3f,sizeof dist);
while(m --){
int a,b,c;
cin >> a >> b >> c; //读入有向图
dist[a][b] = min(dist[a][b],c); //保留距离最短的边
}
floyd();
return 0;
}
spfa算法(可以算负权图)
变量声明
n, N 图的点
m, M 图的边
start 起始点
链式前向星edge x 点下标, v 边权值, next 连接点
vis[ i ] 标记从起始点到点 i 的最短路径是否已经更新
dis[ i ] 表示从起始点到点 i 的最短路径值
queue<int>q; 存放点下标的队列
过程描述:
1.更新起始点 dis 为 0,放进队列
2.从队列中取出一个点
3.用取出的点更新所有与其相邻的点的 dis 。并且,如果当前队列中没有新更新过的点,就将新更新的点放进队列
4.重复2、3操作,直到队列为空
基本实现:
目标:
读入一个含有 n 个点的无负权无向图,求出图中从起始点 start 到任意点的最短路径
代码:
#include<bits/stdc++.h>
using namespace std;
//边&点
#define N 100000
#define M 200000
int n, m, start;
//链式前向星存图
int cnt = 0, head[M+1];
struct Node{
int x, v, next;
}edge[2*N+1];
void addedge(int x, int y, int v)
{
edge[++cnt].v = v;
edge[cnt].x = y;
edge[cnt].next = head[x];
head[x] = cnt;
}
//
int dis[N+1];
bool vis[N+1];
queue<int>q;
//SPFA
void spfa(int st)
{
//起点初始化,放进队列
dis[st] = 0; vis[st] = 1;
q.push(st);
while(!q.empty())
{
//拿出队首元素
int x = q.front(); q.pop();
vis[x] = false;
//更新最短路径值
for(int i = head[x]; i != -1; i = edge[i].next){
int ne = edge[i].x;
if(dis[ne] > dis[x] + edge[i].v){
dis[ne] = dis[x] + edge[i].v;
//如果该元素现在不在队列,放进队列
if(!vis[ne]){
q.push(ne);
vis[ne] = true;
}
}
}
}
}
int main(void)
{
memset(dis, 0x3f, sizeof(dis));
memset(vis, false, sizeof(vis));
memset(head, -1, sizeof(head));
//存图
scanf("%d%d", &n, &m);
for(int i = 1; i <= m; i++){
int x, y, v;
scanf("%d%d%d", &x, &y, &v);
addedge(x, y, v);
addedge(y, x, v);
}
scanf("%d", &start);
spfa(start);
//输出计算结果
for(int i = 1; i <= n; i++){
printf("dis %d: %2d ", i, dis[i]);
if(i %2 == 0) cout <<endl;
}
return 0;
}
其他图
欧拉图
欧拉回路:在一个连通图里,每个边走且只走一次的回路
欧拉图就是有欧拉回路的图
哈密顿图
哈密顿回路:在一个图里,每个点走且只走一次的回路
哈密顿图就是有哈密顿回路的图
二分图
在一张图中,如果能够把全部的点分到 两个集合 中,保证两个集合内部没有 任何边 ,图中的边 只存在于两个集合之间,这张图就是二分图
染色法(判断该图是否是二分图)
bool dfs(int u, int c) {
color[u] = c;//当前点先染色
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];//对于这个点连接的所有的点
if (color[j]) {//如果已经被染过色了
if (color[j] == c)return false;
//就需要判断一下,如果两点颜色一样,染色就冲突了
}
else if (!dfs(j, 3 - c))return false;
//否则dfs去染下一个结点,赋予的颜色肯定要跟 c 不一样
//3 - 1 == 2,3 - 2 == 1
//同时传回染色成功与否的信息
}
return true;
}
bool check() {
memset(color, 0, sizeof color);//0 —— 未染色,1 —— 黑色,2 —— 白色
for (int i = 1; i <= n; i++)
if (color[i] == 0)//一旦某个点没染过色,dfs去染色
if (!dfs(i, 1))return false;//如果传回false显然失败,此图不是二分图
return true;
//否则true
}
原理就是,用 黑 与 白 这两种颜色对图中点染色(相当于给点归属一个集合),一个点显然不能同时具有两种颜色,若有,此图就不是二分图
遍历了这张图的点和边,时间复杂度O ( n + m )
查找
折半查找
被查找的序列必须是按条件有序
//找x
//返回第一个大于等于x的位置
while(l < r){
int mid = (l + r) >> 1;
if(mid >= x) r = mid;
else l = mid + 1;
}
//返回第一个小于等于x的位置
while ( l < r ){
int mid = l + r + 1>> 1;
if ( q[mid] <= x) l = mid;
else r = mid - 1;
}
分块查找
将原来的表拆分成n个表(分块)
将每个表中权值最大的元素作为该表的关键字
find,先通过每个表的关键字定位到正确表中,再进行查找
散列表查找
开放寻址法和拉链法
emmm其实就是哈希表、
直接上代码
//开放寻址法
#include <cstring>
#include <iostream>
using namespace std;
const int N = 200003, null = 0x3f3f3f3f;
int h[N];
int find(int x)
{
int t = (x % N + N) % N;
while (h[t] != null && h[t] != x)
{
t ++ ;
if (t == N) t = 0;
}
return t;
}
int main()
{
memset(h, 0x3f, sizeof h);
int n;
scanf("%d", &n);
while (n -- )
{
char op[2];
int x;
scanf("%s%d", op, &x);
if (*op == 'I') h[find(x)] = x;
else
{
if (h[find(x)] == null) puts("No");
else puts("Yes");
}
}
return 0;
}
//拉链法
#include <cstring>
#include <iostream>
using namespace std;
const int N = 100003;
int h[N], e[N], ne[N], idx;
void insert(int x)
{
int k = (x % N + N) % N;
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
int main()
{
int n;
scanf("%d", &n);
memset(h, -1, sizeof h);
while (n -- )
{
char op[2];
int x;
scanf("%s%d", op, &x);
if (*op == 'I') insert(x);
else
{
if (find(x)) puts("Yes");
else puts("No");
}
}
return 0;
}
冲突处理办法
拉链法:将模除余数相同的数组成链表
开放寻址法:可以理解为厕所找坑。先找适宜的位置,若位置有人,去下一位置。
注意:
开放寻址法在删除结点的时候不能直接置空,否则将截断在它之后填入散列表的同义词结点的查找路径,可以做一个“删除标记”,进行逻辑删除。
排序
- 稳定排序:插入、冒泡、基数、归并
- 不稳定排序:希尔、选择、快排、堆
直接上图
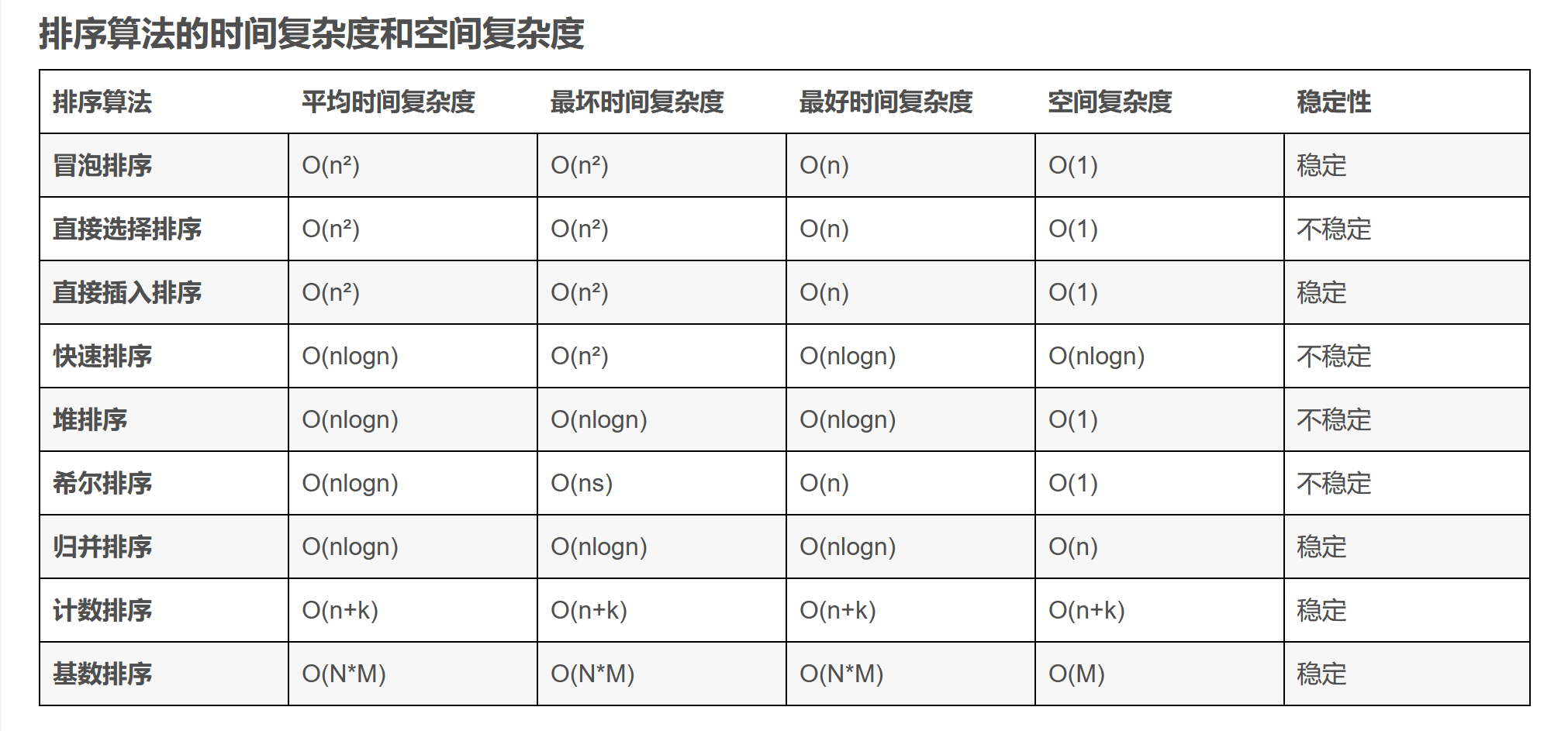
稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r [i]=r [j],且r [i]在r [j]之前,而在排序后的序列中,r [i]仍在r [j]之前,则称这种排序算法是稳定的;否则称为不稳定的
稳定排序
冒泡排序
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
核心代码
//array[]为待排序数组,n为数组长度
void BubbleSort(int array[], int n)
{
int i, j, k;
for(i=0; i<n-1; i++)
for(j=0; j<n-1-i; j++)
{
if(array[j]>array[j+1])
{
k=array[j];
array[j]=array[j+1];
array[j+1]=k;
}
}
}
增加一个swap的标志,当前一轮没有进行交换时,说明数组已经有序,没有必要再进行下一轮的循环了,直接退出
优化版
public static void bubbleSort(int[] arr) {
int temp = 0;
boolean swap;
for (int i = arr.length - 1; i > 0; i--) { // 每次需要排序的长度
swap=false;
for (int j = 0; j < i; j++) { // 从第一个元素到第i个元素
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swap=true;
}
}//loop j
if (swap==false){
break;
}
}//loop i
}// method bubbleSort
插入排序
算法描述
- 把待排序的数组分成已排序和未排序两部分,初始的时候把第一个元素认为是已排好序的。
- 从第二个元素开始,在已排好序的子数组中寻找到该元素合适的位置并插入该位置。
- 重复上述过程直到最后一个元素被插入有序子数组中。
核心代码
public static void insertionSort(int[] arr){
for (int i=1; i<arr.length; ++i){
int value = arr[i];
int position=i;
while (position>0 && arr[position-1]>value){
arr[position] = arr[position-1];
position--;
}
arr[position] = value;
}//loop i
}
归并排序
算法描述
递归法(Top-down)
- 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤3直到某一指针到达序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
核心代码
//tmp数组作用是转存,将q数组排序
void merge_sort(int q[], int l, int r)
{
if(l >= r) return;
int mid = l + r + 1>> 1;//注意mid是向上取整
merge_sort(q, l, mid - 1 ), merge_sort(q, mid, r);
int k = 0, i = l, j = mid, tmp[r - l + 1];
while(i < mid && j <= r)
if(q[i] <= q[j]) tmp[k++] = q[i++];
else tmp[k++] = q[j++];
while(i < mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}
计数排序
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法描述
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1
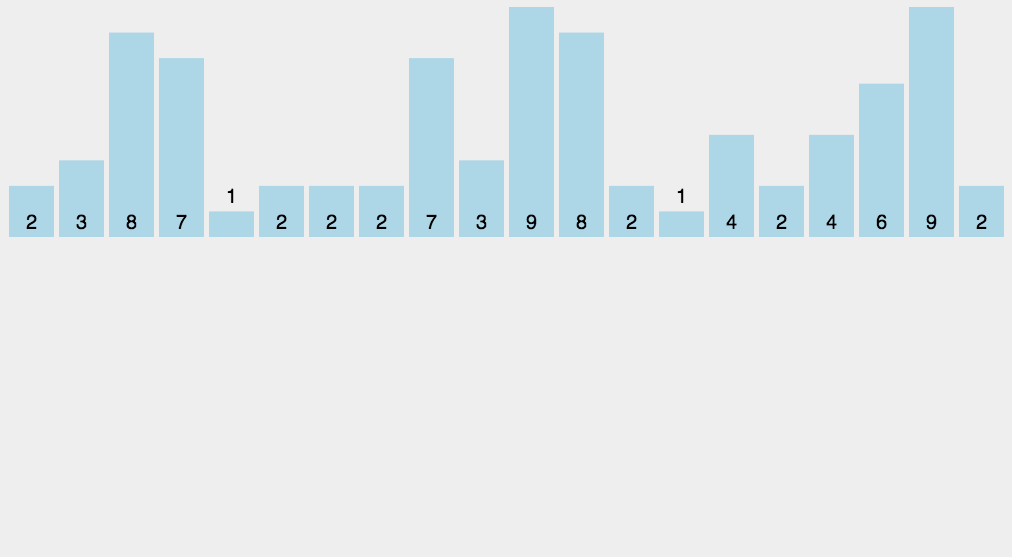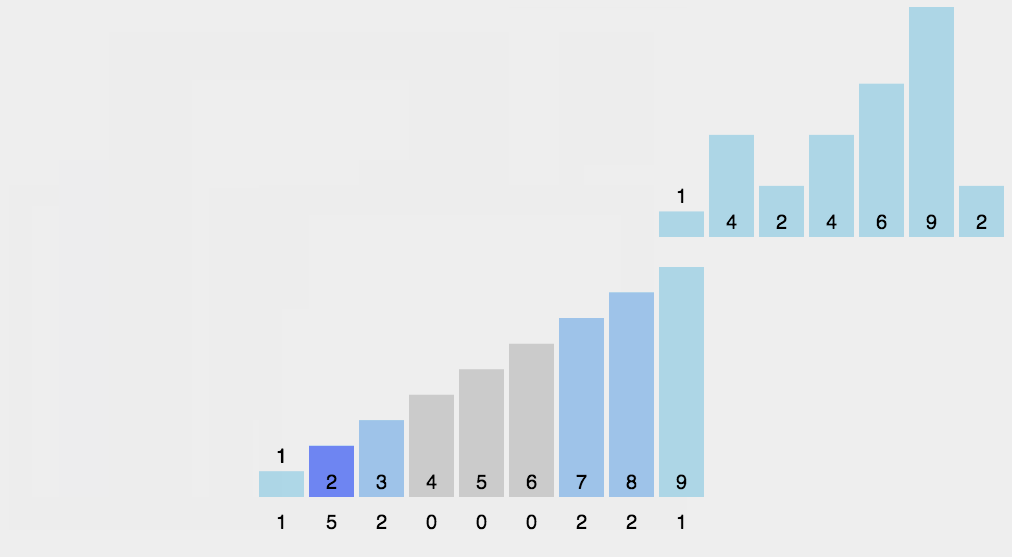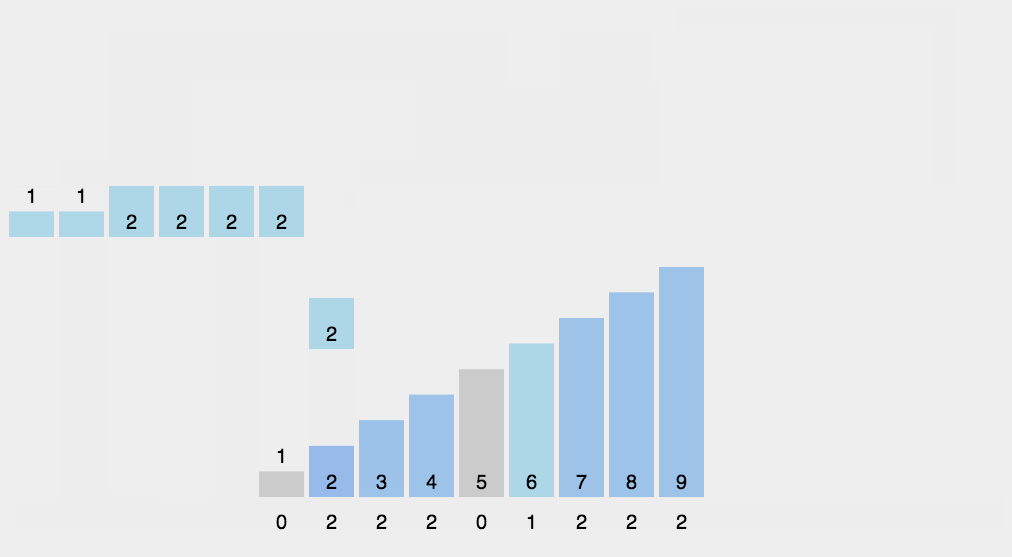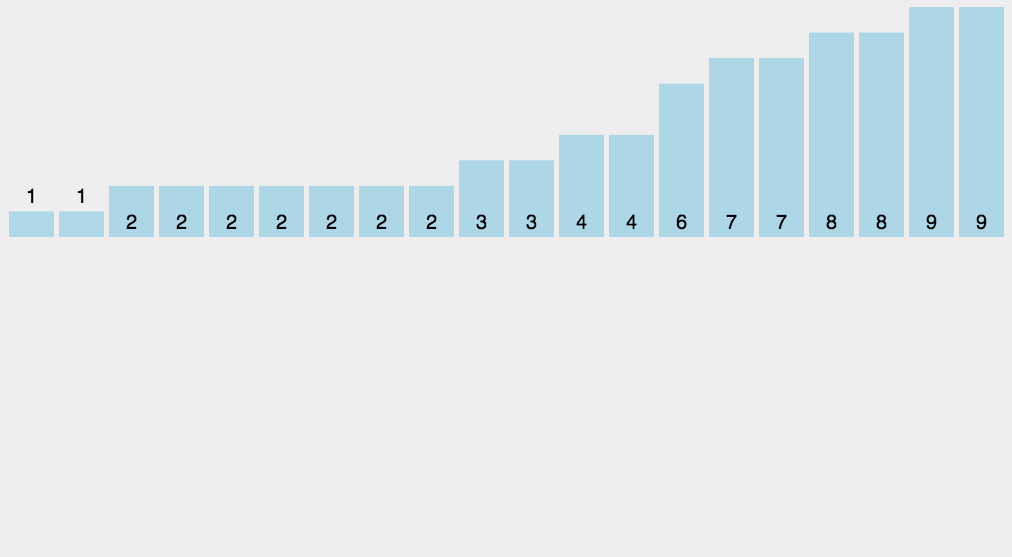
核心代码
public static void countSort(int[] a, int max, int min) {
int[] b = new int[a.length];//存储数组
int[] count = new int[max - min + 1];//计数数组
for (int num = min; num <= max; num++) {
//初始化各元素值为0,数组下标从0开始因此减min
count[num - min] = 0;
}
for (int i = 0; i < a.length; i++) {
int num = a[i];
count[num - min]++;//每出现一个值,计数数组对应元素的值+1
}
for (int num = min + 1; num <= max; num++) {
//加总数组元素的值为计数数组对应元素及左边所有元素的值的总和
count[num - min] += sum[num - min - 1]
}
for (int i = 0; i < a.length; i++) {
int num = a[i];//源数组第i位的值
int index = count[num - min] - 1;//加总数组中对应元素的下标
b[index] = num;//将该值存入存储数组对应下标中
count[num - min]--;//加总数组中,该值的总和减少1。
}
//将存储数组的值一一替换给源数组
for(int i=0;i<a.length;i++){
a[i] = b[i];
}
}
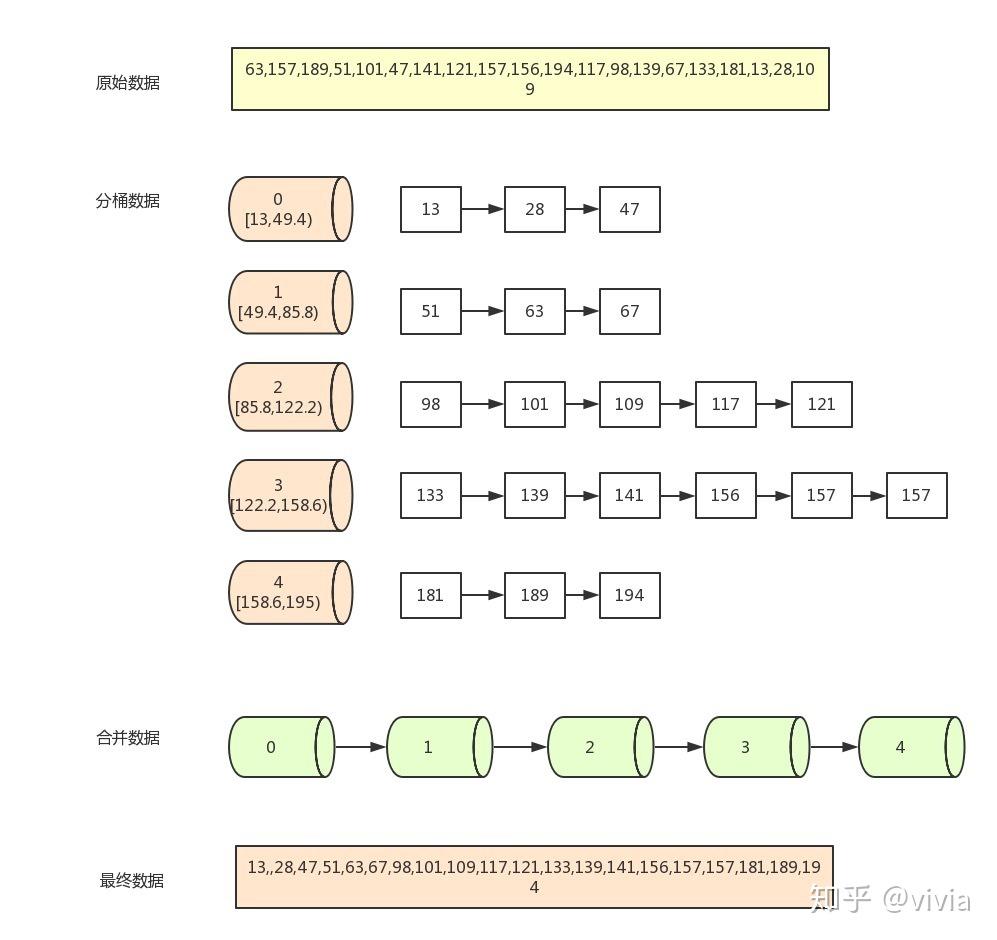
桶排序
桶排序又叫箱排序,是计数排序的升级版,它的工作原理是将数组分到有限数量的桶子里,然后对每个桶子再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序),最后将各个桶中的数据有序的合并起来。
计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。网络中很多博文写的桶排序实际上都是计数排序,并非标准的桶排序,要注意辨别。
算法描述
- 找出待排序数组中的最大值max、最小值min
- 我们使用 动态数组ArrayList 作为桶,桶里放的元素也用 ArrayList 存储。桶的数量为(max-min)/arr.length+1
- 遍历数组 arr,计算每个元素 arr[i] 放的桶
- 每个桶各自排序
- 遍历桶数组,把排序好的元素放进输出数组
核心代码
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
System.out.println(bucketArr.toString());
}
桶排序的稳定性依赖于子排序的稳定性
基数排序
基数排序(Radix Sort)是桶排序的扩展,它的基本思想是:将整数按位数切割成不同的数字,然后按每个位数分别比较。
排序过程:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
算法描述
- 取得数组中的最大数,并取得位数;
- arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序(利用计数排序适用于小范围数的特点);

核心代码
public abstract class Sorter {
public abstract void sort(int[] array);
}
public class RadixSorter extends Sorter {
private int radix;
public RadixSorter() {
radix = 10;
}
@Override
public void sort(int[] array) {
// 数组的第一维表示可能的余数0-radix,第二维表示array中的等于该余数的元素
// 如:十进制123的个位为3,则bucket[3][] = {123}
int[][] bucket = new int[radix][array.length];
int distance = getDistance(array); // 表示最大的数有多少位
int temp = 1;
int round = 1; // 控制键值排序依据在哪一位
while (round <= distance) {
// 用来计数:数组counter[i]用来表示该位是i的数的个数
int[] counter = new int[radix];
// 将array中元素分布填充到bucket中,并进行计数
for (int i = 0; i < array.length; i++) {
int which = (array[i] / temp) % radix;
bucket[which][counter[which]] = array[i];
counter[which]++;
}
int index = 0;
// 根据bucket中收集到的array中的元素,根据统计计数,在array中重新排列
for (int i = 0; i < radix; i++) {
if (counter[i] != 0)
for (int j = 0; j < counter[i]; j++) {
array[index] = bucket[i][j];
index++;
}
counter[i] = 0;
}
temp *= radix;
round++;
}
}
private int getDistance(int[] array) {
int max = computeMax(array);
int digits = 0;
int temp = max / radix;
while(temp != 0) {
digits++;
temp = temp / radix;
}
return digits + 1;
}
private int computeMax(int[] array) {
int max = array[0];
for(int i=1; i<array.length; i++) {
if(array[i]>max) {
max = array[i];
}
}
return max;
}
}
不稳定排序
快速排序
算法描述
- 从数列中挑出一个元素,称为"基准"(pivot),
- 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
- 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序
核心代码
void quick_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第二步:递归处理子问题
quick_sort(q, l, j), quick_sort(q, j + 1, r);
//第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤
}
选择排序
算法描述
- 在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
- 从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
- 重复第二步,直到所有元素均排序完毕。
核心代码
public static void selectionSort(int[] arr) {
int temp, min = 0;
for (int i = 0; i < arr.length - 1; i++) {
min = i;
// 循环查找最小值
for (int j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
if (min != i) {
temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
}
堆排序
堆的概念
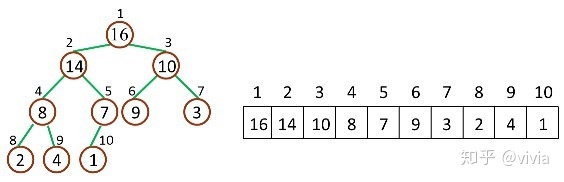
堆是一种特殊的完全二叉树(complete binary tree)。完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示(普通的一般的二叉树通常用链表作为基本容器表示),每一个结点对应数组中的一个元素。
堆排序原理
-
堆排序就是把最大堆堆顶的最大数取出,将剩余的堆继续调整为最大堆,再次将堆顶的最大数取出,这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作:
- 最大堆调整(Max-Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build-Max-Heap):将堆所有数据重新排序,使其成为最大堆
- 堆排序(Heap-Sort):移除位在第一个数据的根节点,并做最大堆调整的递归运算 继续进行下面的讨论前,需要注意的一个问题是:数组都是 Zero-Based,这就意味着我们的堆数据结构模型要发生改变
所以:
- Parent(i) = floor((i-1)/2),i 的父节点下标
- Left(i) = 2i + 1,i 的左子节点下标
- Right(i) = 2(i + 1),i 的右子节点下标
核心代码
public class ArrayHeap {
private int[] arr;
public ArrayHeap(int[] arr) {
this.arr = arr;
}
private int getParentIndex(int child) {
return (child - 1) / 2;
}
private int getLeftChildIndex(int parent) {
return 2 * parent + 1;
}
private void swap(int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
/**
* 调整堆。
*/
private void adjustHeap(int i, int len) {
int left, right, j;
left = getLeftChildIndex(i);
while (left <= len) {
right = left + 1;
j = left;
if (j < len && arr[left] < arr[right]) {
j++;
}
if (arr[i] < arr[j]) {
swap(array, i, j);
i = j;
left = getLeftChildIndex(i);
} else {
break; // 停止筛选
}
}
}
/**
* 堆排序。
* */
public void sort() {
int last = arr.length - 1;
// 初始化最大堆
for (int i = getParentIndex(last); i >= 0; --i) {
adjustHeap(i, last);
}
// 堆调整
while (last >= 0) {
swap(0, last--);
adjustHeap(0, last);
}
}
}
希尔排序
算法描述
- 选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
- 按增量序列个数k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
核心代码
//下面是插入排序
void InsertSort( int array[], int n)
{
int i,j,temp;
for( i=0;i<n;i++ )
{
if(array[i]<array[i-1])
{
temp=array[i];
for( j=i-1;array[j]>temp;j--)
{
array[j+1]=array[j];
}
array[j+1]=temp;
}
}
}
//在插入排序基础上修改得到希尔排序
void SheelSort( int array[], int n)
{
int i,j,temp;
int gap=n;
do{
gap=gap/3+1;
for( i=gap;i<n;i++ )
{
if(array[i]<array[i-gap])
{
temp=array[i];
for( j=i-gap;array[j]>temp;j-=gap)
{
array[j+gap]=array[j];
}
array[j+gap]=temp;
}
}
}while(gap>1);
}
结语
光阴如骏马加鞭,日月如落花流水。比起在生活中被人左右情绪,我希望你们更喜欢无人问津的时光。待到秋来九月八,我花开后百花杀。愿我们在不久的将来遇见更好的自己


 浙公网安备 33010602011771号
浙公网安备 33010602011771号