FFT小记

最近被迫学习了一些多项式的知识，这篇文章算是把个人的理解写了下来吧，应该会有很多可以练习的题目。

多项式基础

多项式初中都学过，其实通俗点说，一个多项式 \(F\) 可以表示为 \(F(x)=a_0+a_1x+a_2x^2+...\)，其中称 \(x^i\) 为多项式的 \(i\) 次项， \(a_i\) 为 \(i\) 次项的系数。

一般来说，我们也常用 \(F[i]\) 来表示 \(a_i\)。

我们称一个多项式为 \(k\) 次多项式当且仅当该多项式系数不为 \(0\) 的次数最高的项的次数为 \(k\)。

多项式的四则运算

注意：多项式的四则运算与数的四则运算一样，都满足 交换律，结合律，分配律

加法 / 减法

显然将对应次项的系数相加/减即可，即 \(F(x)\pm G(x)=\sum\limits_{i=0}(F[i]\pm G[i])x^i\)

ps:关于为什么这里的 \(\sum\) 没有上界，可以理解为所有多项式都有 \(\infty\) 次项，但是大部分项的系数都是 \(0\)

乘法

多项式的乘法也叫多项式的加法卷积。

卷积的符号为 \(\ast\)，两个多项式 \(F,G\) 的卷积即 \(F \ast G\)。

设 \(S=F \ast G\)，则 \(S[k]=\large\sum\limits_{\normalsize{i\oplus j=k}}\normalsize{F[i]G[j]}\)，其中 \(\oplus\) 为某一种运算符号。

多项式乘法中的 \(\oplus\) 就是 \(+\)，即 \(S[k]=\large\sum\limits_{\normalsize{i+j=k}}\normalsize{F[i]G[j]}\)

所以多项式乘法叫做多项式的加法卷积。

除法

根据小学知识可得，\(\dfrac{F}{G}=F\times G^{-1}\)。

因此对多项式 \(G\) 求逆，然后与 \(F\) 卷起来即可。

具体怎么求逆请继续向下阅读

快速傅里叶变换

快速傅里叶变换就是所谓的 FFT （Fast Fast TLE），能够在 \(\text{O}(n \log n)\) 的复杂度里将两个多项式乘起来。

点值表示法

一个 \(n\) 次多项式一定可以由 \(n+1\) 个不同的点唯一的表示出。

这是显然的，因为把这几个点值带进去就能组成一个有 \(n+1\) 个方程 \(n+1\) 元方程组，那么这个方程显然有唯一解。

我们将 \(n\) 次多项式 \(F\) 的点值表示记为 \(F(x)=\left\{(x_0,y_0),(x_1,y_1),...,(x_k,y_k)\right\}\)

如果我们知道 \(n\) 次多项式 \(F\) 和 \(m\) 次多项式 \(G\) 的点值表示为

\[F(x)=\left\{(x_0,F(x_0)),(x_1,F(x_1)),...,(x_n,F(x_{n+m}))\right\} \]

\[G(x)=\left\{(x_0,G(x_0)),(x_1,G(x_1)),...,(x_m,G(x_{n+m}))\right\} \]

那么想一想就会发现 \(F \ast G\) 的点值表示就是

\[F(x) \ast G (x)=\left\{(x_0,F(x_0)G(x_0)),(x_1,F(x_0)G(x_0)),...,(x_m,F(x_{n+m})G(x_{n+m}))\right\} \]

而计算这个点值表示是 \(\text{O}(n)\) 的。

只要我们再把这个点值表示转化称多项式的形式，卷积运算就完成了。

那么问题显而易见，转化为了怎么将一个多项式转化为点值表示以及怎么将点值表示转化为多项式。

我们称上面这两种操作为 DFT 和 IDFT。

单位复根

前置知识：虚数，向量（不知道的一定要先学完这两个知识再继续向下看）

多项式转化为点值很容易，随便选几个值带进多项式就行了，但这样的复杂度是 \(\text{O}(n^2)\) 的，不能接受。

注意到带入多项式的值是可以自己决定的，所以可以带入一些有特殊性质的数，比如 \(1\)，\(-1\)，即单位根。

但是两个数肯定不够用，因此我们考虑扩展数的范围。

我们常见的数都是实数，即都可以在一个一个一位空间（数轴）上一一对应表示出来，那么如果我们把一位拓展成二维，便可以引入一种新数 —— 虚数。

这样原先的一位空间便成为了二维空间（即复平面），我们继续在这上面找有特殊性质的数。

复数也有乘法运算，我们看看复数乘法有没有什么好的性质。

\[\begin{aligned}(a+bi)\times(c+di)&=ac+adi+bci-bd\\&=ac-bd+(ad+bc)i\end{aligned} \]

点的对应关系为 \((a,b)\times(c,d)=(ac-bd,ad+bc)\)

直接从数值上看可能看不出什么，所以我们带入可以画图举例。

如果有两个点 \(B(1,2),C(3,1)\)，令 \(A=B \times C\)，则 \(A(1,7)\)，如图所示：

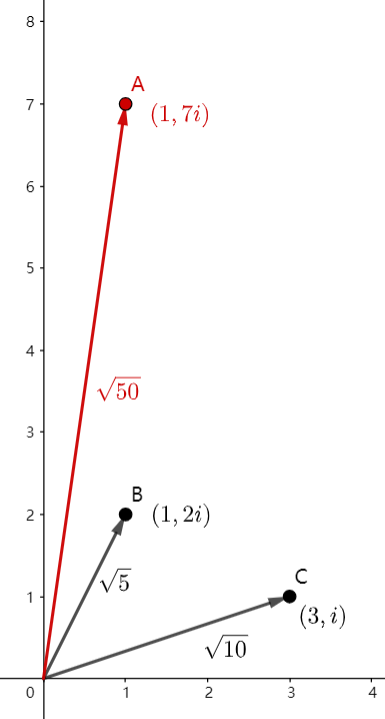
发现了吗，\(|AO|=|BO| \times |CO|\)，这是个很好的性质。

严谨起见，我们现在来证明一下。

证明

假设有两个点 $A(a,b),B(c,d)$，令 $C$ 为 $A \times B$ 即 $(ac-bd,ad+bc)$。

根据勾股定理，有

\[\begin{aligned} |AO|^2&=a^2+b^2\\ |BO|^2&=c^2+d^2\\ \\ (|AO|\times|BO|)^2&=|AO|^2\times|BO|^2\\ &=a^2c^2+a^2d^2+b^2c^2+b^2d^2\\ \\ |CO|^2&=(ac-bd)^2+(ad+bc)^2\\ &=a^2c^2+b^2d^2-2abcd+a^2d^2+b^2c^2+2abcd\\ &=a^2c^2+a^2d^2+b^2c^2+b^2d^2\\ &=(|AO|\times|BO|)^2\\ \\ \therefore |CO|&=|AO|\times |BO| \end{aligned}\]

证毕。

事实上，虚数相乘还有辐角（即顺时针转到 \(x\) 轴正半轴需要转的角度）相加的性质（可以看图理解）。

那么如果我们选择作为根的点为 \(D\)，那么如果 \(|DO|=1\) ，那么这就有了和 \(1,-1\) 一样的性质。显然满足这个条件的 \(D\) 都在以 \(O\) 为圆心，半径为 \(1\) 的圆上，我们称这个圆为单位圆。

而且圆上有 \(\infty\) 个点，所以我们就有取之不尽的单位根了。

那么如果我们要对 \(n\) 次多项式进行 DFT，那么就要在单位圆上选出 \(n\) 个点，让这几个点恰好将单位圆 \(n\) 等分，其实就是求 \(x^n=1\) 这个方程在实数范围内的 \(n\) 个根（代数基本定理）。

我们设 \(\omega_n\) 为模长为 \(1\)，辐角为 \(\frac{360}{n}^{\circ}\) 的虚数，则 \(\omega_n^i\) 就是模长为 \(1\) ，辐角为 \(\frac{360 \times i}{n}^{\circ}\) 的虚数（虚数相乘辐角相加），所以我们需要的 \(n\) 个单位根就分别是 \(\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}\)。

事实上，\(\omega_n^i\) 中的 \(i\) 并非一定满足 \(i < n\)，因为 \(\omega_n^i=\omega_n^{i\ \text{mod}\ n}\) （因为每 \(n\) 个单位根就相当于转了一圈）

那么我们应该如何计算 \(\omega_n\) 呢？

事实上直接套欧拉公式就行了，即 \(\omega_n=e^{\frac{2\pi i}{n}}=\cos\left(\dfrac{2\pi}{n}\right)+i \times\sin\left(\dfrac{2\pi}{n}\right)\)

现在我们来看看单位根都有哪些好的性质。

• \(\omega^n_n=1,\omega^n_{2n}=-1\)

  \(\omega^n_n\) 相当于转了 \(360^{\circ}\) 也就等于没转，所以辐角是 \(0^{\circ}\) 也就是在 \(x\) 的正半轴上。

  \(\omega^n_{2n}\) 相当于转了 \(180^{\circ}\) 也就是在 \(x\) 的负半轴上。

• \(\omega_n^m=\omega_{2n}^{2m}\)

  从图像上考虑，等号两边模长相等，辐角都是 \(\frac{m}{n}\)，故相等。

• \(\omega_{2n}^{n+m}=-\omega_{2n}^m\)

  简单化一化就出来了：

\[\begin{aligned} \omega_{2n}^{n+m}&=\omega_{2n}^n \times \omega_{2n}^m\\ &=-1 \times \omega_{2n}^m\\ &=-\omega_{2n}^m \end{aligned}\]

这些性质都会在接下来的 DFT 过程中起很大的作用。

DFT

DFT 是一个用分治的方式将一个多项之转化为单位根的点值表示的算法。

注意，DFT是线性变换，即满足：

1. \(\text{DFT}(x+y)=\text{DFT}(x)+\text{DFT}(y)\)
2. \(\text{DFT}(ax)=a\times \text{DFT}(x)\) （这里的 \(a\) 是常数而非多项式）

在分治的过程中，DFT 的分治方式并不同与一般的分治，左边一半右边一半地进行分治，而是将多项式的奇数次项与偶数次项分别进行分治。如果这样分治，如果要使分治两边均匀，那么多项式的次数就必须是 \(2\) 的整数次幂，但一般给定的多项式不会满足这个条件，所以我们要在多项式后面补系数为 \(0\) 的项，知道其次数为 \(2\) 的整数次幂。

下面我们进行保姆级详细的推式子

我们假设下面的 \(n\) 均为 \(2\) 的整数次幂。

假设我们有多项式 \(F\)：

\[F(x)=a_0+a_1x+a_2x^2+\cdot+a_nx^n \]

我们将其奇数项与偶数项分别设出多项式 \(G_0,G_1\)：

\[G_0(x)=a_0+a_2x+a_4x+\cdot+a_nx^{n/2} \]

\[G_1(x)=a_1+a_3x+a_5x+\cdot+a_{n-1}x^{n/2} \]

那么显然有：

\[F(x)=G_0(x^2)+x \times G_1(x^2) \]

将等式两边同时进行DFT变换，并带入单位根 \(\omega_n^m\) 得：

\[\begin{aligned} \text{DFT}(F(\omega_n^m)) &= \text{DFT}(G_0((\omega_n^m)^2))+\omega_n^m \times \text{DFT}(G_1((\omega_n^m)^2))\\ &= \text{DFT}(G_0(\omega_n^{2m}))+\omega_n^m \times \text{DFT}(G_1(\omega_n^{2m}))\\ &= \text{DFT}(G_0(\omega_{n/2}^m))+\omega_n^m \times \text{DFT}(G_1(\omega_{n/2}^m)) \end{aligned}\]

\[\begin{aligned} \text{DFT}(F(\omega_n^{m+n/2})) &= \text{DFT}(G_0((\omega_n^{m+n/2})^2))+\omega_n^{m+n/2} \times \text{DFT}(G_1((\omega_n^{m+n/2})^2))\\ &= \text{DFT}(G_0(\omega_n^{2m+n}))+\omega_n^{m+n/2} \times \text{DFT}(G_1(\omega_n^{2m+n}))\\ &= \text{DFT}(G_0(\omega_n^{(2m+n)\ \text{mod}\ n}))+\omega_{2n}^{2m+n} \times \text{DFT}(G_1(\omega_n^{(2m+n)\ \text{mod}\ n}))\\ &= \text{DFT}(G_0(\omega_n^{2m}))-\omega_{2n}^{2m} \times \text{DFT}(G_1(\omega_n^{2m}))\\ &= \text{DFT}(G_0(\omega_{n/2}^{m}))-\omega_{n}^{m} \times \text{DFT}(G_1(\omega_{n/2}^{m})) \end{aligned}\]

根据这两个公式，我们只要求出 \(\text{DFT}(G_0(\omega_{n/2}^m))\) 和 \(\text{DFT}(G_1(\omega_{n/2}^m))\)，我们就能推出 \(\text{DFT}(F(\omega_n^m))\) 与 \(\text{DFT}(F(\omega_n^{m+n/2}))\)，而前两者同样可以递归去求。

这样我们那就完成了 DFT 的全部过程。

代码实现

复数运算

首先因为 DFT 要涉及复数运算，所以要手写复数，虽然STL有复数类，但是那个常熟太大，最好别用。

struct complex
{
	double x,y;
	complex operator + (complex p)const{return complex{x+p.x,y+p.y};}
	complex operator - (complex p)const{return complex{x-p.x,y-p.y};}
	complex operator * (complex p)const{return complex{x*p.x-y*p.y,y*p.x+x*p.y};}
};

递归

递归总要有边界条件，这里的边界条件显然是 \(n=1\) 的情况，而此时多项式只有一个常数项，所以直接范围即可。

if(n==1) return;

按照上面的做法，首先将多项式的奇数次项与偶数次项分离，然后分别对两边进行 DFT

complex c[(n>>1)+5],d[(n>>1)+5];
for(int i=0;i<=n;i+=2)
{
	c[i>>1]=a[i];
	d[i>>1]=a[i+1];
}
fft(n>>1,c,id);
fft(n>>1,d,id);

接下来按照上面推出的式子，用 \(\text{DFT}(G_0(\omega_{n/2}^m))\) 和 \(\text{DFT}(G_1(\omega_{n/2}^m))\)，计算出 \(\text{DFT}(F(\omega_n^m))\) 与 \(\text{DFT}(F(\omega_n^{m+n/2}))\)

这里的 \(w\) 即单位根 \(\omega_n\)，\(j\) 用来计算单位根的幂 \(\omega_n^m\)。

complex w=complex{cos(2.0*Pi/n),sin(2.0*Pi/n)},j=complex{1,0};
for(int i=0;i<(n>>1);++i,j=j*tmp)
{
	a[i]=c[i]+j*d[i];
	a[i+(n>>1)]=c[i]-j*d[i];
}

这样一套下来，DFT就做完了。

完整代码（递归版）

const int N=4e6+5;
const double Pi=acos(-1.0);

struct complex
{
	double x,y;
	complex operator + (complex p)const{return complex{x+p.x,y+p.y};}
	complex operator - (complex p)const{return complex{x-p.x,y-p.y};}
	complex operator * (complex p)const{return complex{x*p.x-y*p.y,y*p.x+x*p.y};}
}a[N],b[N];

void fft(int n,complex a[])
{
	if(n==1) return;
	complex c[(n>>1)+5],d[(n>>1)+5];
	for(int i=0;i<=n;i+=2)
	{
		c[i>>1]=a[i];
		d[i>>1]=a[i+1];
	}
	fft(n>>1,c,id);
	fft(n>>1,d,id);
	complex w=complex{cos(2.0*Pi/n),sin(2.0*Pi/n)},j=complex{1,0};
	for(int i=0;i<(n>>1);++i,j=j*w)
	{
		a[i]=c[i]+j*d[i];
		a[i+(n>>1)]=c[i]-j*d[i];
	}
}

IDFT

先说结论：

把 DFT 过程中的 \(\omega_n^m\) 换成 \(\omega_n^{-m}\)，并在最后除以 \(n\)。

即 DFT 的式子是这样的：

\[\text{DFT}(F)[i]=\sum\limits_{j=0}^{n-1}(\omega_n^i)^jF[j] \]

而 IDFT 的式子是这样的：

\[F[i]=n^{-1} \times \sum\limits_{j=0}^{n-1}(\omega_n^{-i})^j\text{DFT}(F)[j] \]

证明就不写了主要是我也不会，感兴趣的可以百度找一找。

那么我们有了这个结论，只要把 DFT 的过程简单改一下就行了。

关于如何计算 \(\omega_n^{-1}\)，还是根据欧拉公式：

\[\omega_n^{-1}=e^{-\frac{2\pi i}{n}}=\cos\left(\dfrac{2\pi}{n}\right)+i \times\sin\left(-\dfrac{2\pi}{n}\right) \]

代码（DFT与IDFT结合）

void fft(int n,complex a[],int id)
//这里的 id 表示是进行 DFT 还是 IDFT。
//如果 id=1 则表示进行 DFT
//如果 id=-1 则表示进行 IDFT
{
	if(n==1) return;
	complex c[(n>>1)+5],d[(n>>1)+5];
	for(int i=0;i<=n;i+=2)
	{
		c[i>>1]=a[i];
		d[i>>1]=a[i+1];
	}
	fft(n>>1,c,id);
	fft(n>>1,d,id);
	complex w=complex{cos(2.0*Pi/n),sin(2.0*id*Pi/n)},j=complex{1,0};
	for(int i=0;i<(n>>1);++i,j=j*w)
	{
		a[i]=c[i]+j*d[i];
		a[i+(n>>1)]=c[i]-j*d[i];
	}
}

ps:这里的fft函数进行IDFT时并没有除以 \(n\)，所以在调用后需要手动除

使用FFT进行卷积

为方便理解，下面的每一步都会跟随着代码实现

假设我们要将 \(n\) 次多项式 \(F\) 与 \(m\) 次多项式 \(G\) 卷起来。

首先我们可以确定的是，卷出来的多项式最多 \(n+m\) 次，所以我们在 DFT 与 IDFT 的过程中都至少要以 \(n+m\) 次为上限，又因为这个上线必须是 \(2\) 的正整数幂次，所以我们要以第一个大于 \(n+m\) 的 \(2\) 的正整数次幂为上限。

int now=1; //now即DFT/IDFT过程的上界
while(now<=n+m)
    now<<=1;

然后将多项式 \(F,G\) 用 DFT 转为点值表示。

fft(now,f,1);
fft(now,g,1);

然后求出 \(F \ast G\) 的点值表示。

for(int i=0;i<=now;i++)
	a[i]=a[i]*b[i];

再把 \(F \ast G\) 的点值表示用 IDFT 转化成系数表示。

fft(now,a,-1);

最后除以 \(n\) 就是 \(F \ast G\) 了。

for(int i=0;i<=n+m;i++)
	a[i].x=(int)(a[i].x/now+0.5);

常数优化

因为 FFT 的过程中涉及到实数运算，且还有函数递归，所以常熟非常大，为了防止被卡常，拥有一个小常熟的 FFT 是非常重要的一件事。

递归变循环

FFT 递归的过程实际上是不断将奇数位与偶数位分离处理，即下面这样的变换：

\[0\ 1\ 2\ 3\ 4\ 5\ 6\ 7\ (n=8) \]

\[0\ 2\ 4\ 6|1\ 3\ 5\ 7\ (n=4) \]

\[0\ 4|2\ 6|1\ 5|3\ 7\ (n=2) \]

\[0|4|2|6|1|5|3|7\ (n=1) \]

因为递归要反着做，所以我们要先求出 \(n=1\) 时的序列，再向上合并。

那么如何求出 \(n=1\) 时的序列呢？这种事情显然是要找规律

可以自己找先试着一下

十进制	二进制
\(0 \rightarrow 0\)	\(000 \rightarrow 000\)
\(1 \rightarrow 4\)	\(001 \rightarrow 100\)
\(2 \rightarrow 2\)	\(010 \rightarrow 010\)
\(3 \rightarrow 6\)	\(011 \rightarrow 110\)
\(4 \rightarrow 1\)	\(100 \rightarrow 001\)
\(5 \rightarrow 5\)	\(101 \rightarrow 101\)
\(6 \rightarrow 3\)	\(110 \rightarrow 011\)
\(7 \rightarrow 7\)	\(111 \rightarrow 111\)

发现了吗？这个变换相当于将数的二进制翻转。

ps：这里的翻转是在长度为 \(\log_2(n)\) 的情况下进行的，位数不足需要在前面补 \(0\)，比如这里的 \(\log_2(n)=3\)，那么 \((2)_2=10=010\)（把二位补成三位）

那么现在已经很容易在 \(\text{O}(n\log n)\) 的复杂度内完成翻转。

事实上，也存在 \(\text{O}(n)\) 的做法，即：

for(int i=0;i<n;i++)
	rev[i]=(rev[i>>1]>>1)|((i&1)?n>>1:0);
//rev[i]就是 i 在翻转后的结果

可以自己思考一下为什么是对的。

既然将奇偶分离已经优化，那么接下来能不能把优化合并的常数。

complex w=complex{cos(2.0*Pi/n),sin(2.0*id*Pi/n)},j=complex{1,0};
for(int i=0;i<(n>>1);++i,j=j*w)
{
	a[i]=c[i]+j*d[i];
	a[i+(n>>1)]=c[i]-j*d[i];
}

显然，上面的 \(c_i\) 即奇偶分离前的 \(a_i\)，\(d_i\) 为奇偶分开前的 \(a_{i+n/2}\)。

所以我们就有了下面的代码：

complex w=complex{cos(2.0*Pi/n),sin(2.0*id*Pi/n)},j=complex{1,0};
for(int i=0;i<(n>>1);++i,j=j*w)
{
	complex tmp=j*a[i+(n>>1)];
	a[i+(n>>1)]=a[k]-tmp;
	a[k]=a[k]+tmp;
}

通过这两个优化，奇偶分离和合并都已经不用新建数组了，所以我们就可以很容易地把递归变成循环来做了。

完整代码（循环版）

const int N=4e6+5;
const double Pi=acos(-1.0);

struct complex
{
	double x,y;
	complex operator + (complex p)const{return complex{x+p.x,y+p.y};}
	complex operator - (complex p)const{return complex{x-p.x,y-p.y};}
	complex operator * (complex p)const{return complex{x*p.x-y*p.y,y*p.x+x*p.y};}
}a[N],b[N];

void fft(int n,complex a[])
{
	for(int i=0;i<n;++i)
		rev[i]=(rev[i>>1]>>1)|((i&1)?now>>1:0);
	for(int i=0;i<n;++i)
		if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int l=2;l<=n;l<<=1)
	{
		int len=l>>1;
		complex w=(clx){cos(2*Pi/l),id*sin(2*Pi/l)};
		for(int i=0;i<n;i+=l)
		{
			complex j=(clx){1,0};
			for(int k=i;k<i+len;++k,j=j*w)
			{
				complex tmp=j*a[len+k];
				a[len+k]=a[k]-tmp;
				a[k]=a[k]+tmp;
			}
		}
	}
}

三次变两次

上面实现多项式卷积的方式需要进行三次 FFT，那运行时间就打大了三倍。但事实上，我们只需要两次 FFT 就能完成同样的任务。

假设我们现在要把多项式 \(F,G\) 给卷起来。

设以 \(F\) 为实部，以 \(G\) 为虚部的复数多项式 \(H(x)=F(x)+G(x)i\)

那么显然有 \(H(x)^2=F(x)^2-G(x)^2+2F(x)G(x)i\)

因此 \(F\ast G\) 就是 \(H^2\) 的虚部除以 \(2\)。

代码就不贴了主要是懒

题目练习

Luogu P3803 【模板】多项式乘法（FFT） （板子）

Luogu P1919 【模板】A*B Problem升级版（FFT快速傅里叶） （板子）

Luogu P3338 [ZJOI2014]力 （多项式在实际中应用的方式与技巧）