二维数点的各种姿势

介绍若干种奇特的二维数点问题。

多边形二维数点

问题形式：给出平面上 n 个点和 m 个凸多边形，求出每个多边形内包含几个给出的点。
若多边形的边一共具有 k 种不同的斜率，则可以转化成 k 次二维数点。
常见的情况是多边形全部相似，比如相似的三角形、平行四边形。
最为简单粗暴的方法：直接像定积分一样容斥，转化成若干个梯形数点。

灵魂画手见谅
比较神秘的方法：

除了这样会使限制变成2-side，我没看出什么优势

斜线二维数点

问题形式：给出若干条斜率为1的线段，询问若干次，每次形如一个矩形内，在给出的线段上的整点数。
不妨设线段不交。将询问差分为向右下的2-side矩形。考虑一条线段对一个矩形的贡献，分几类讨论：

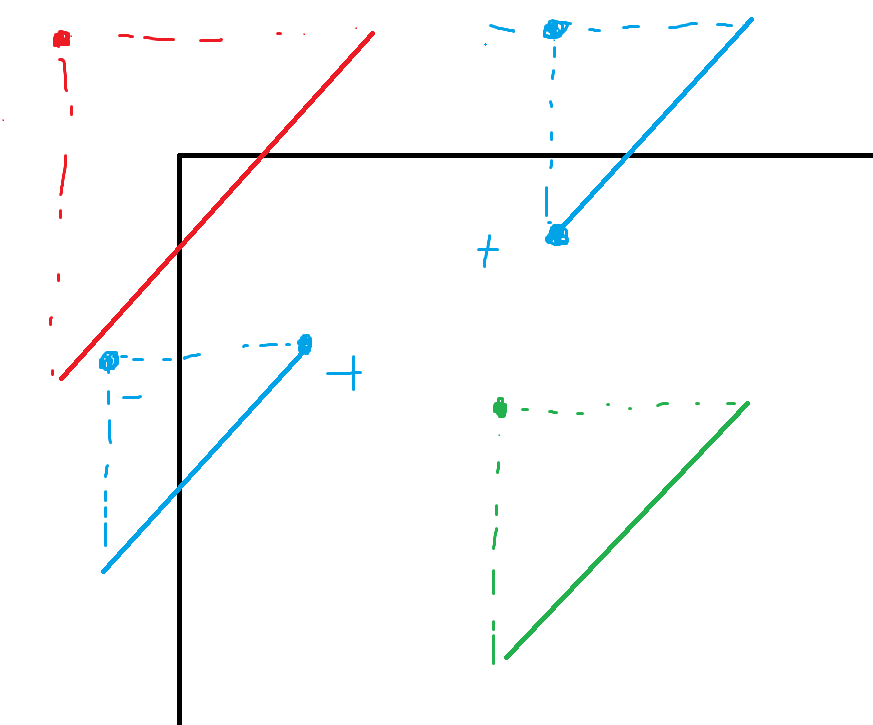
容易发现，分类后，贡献可以表为询问点坐标和关于线段的一些“关键点”坐标的线性组合。
于是我们将一条线段的贡献挂在若干关键点上，再分类考虑贡献即可。

真·斜线二维数点

PKUSC2022 D1T2。由于博主是鸽子，这部分鸽了。

单调递增二维数点

问题形式：给出平面上若干条水平线段，使得纵坐标单调递减时，左右端点横坐标均单调递增；询问若干次，形如一个向右下的2-side矩形内，在给出的线段上的整点数。
（不妨假设值域和点数同阶；线段、矩形端点均在第一象限；一个纵坐标恰有一条水平线段）
时间复杂度要求线性。
将一条水平线段差分成两条从 \(y=0\) 开始的水平线段，分开做正贡献和负贡献的线段。
从下往上扫描线，维护当前扫描线上每个点所对应的向右下2-side矩形内的点数。但是不维护横坐标小于（当前扫描线上的那条水平线段的右端点）的点。
例子：lg8283
彩蛋：lxl和例子的出题人的聊天记录