第三节 金融期权价值评估

第一编 财务管理

第六章 期权价值评估

第三节 金融期权价值评估

一、金融期权价值的影响因素★★

（一）期权的内在价值和时间溢价

1. 期权的内在价值

详细介绍

期权的内在价值，是指期权立即执行产生的经济价值。内在价值的大小，取决于期权标的资产的现行市价与期权执行价格的高低。内在价值不同于到期日价值，期权的到期日价值取决于到期日标的股票市价与执行价格的高低。如果现在巳经到期，则内在价值与到期日价值相同。

对于看涨期权来说，现行资产价格高于执行价格时，立即执行期权能够给持有人带来净收入，其内有价值为现行价格与执行价格的差额（\(S_0-X\))。如果资产的现行市价等于或低于执行价格时，立即执行不会给持有人带来净收入，持有人也不会去执行期权，此时看涨期权的内在价值为0。例如，看涨期权的执行价格为1Q0元，现行价格为120元，其内在价值为2D元（120-100)。如果现行价格变为80元，则内在价值为0。

对于看跌期权来说，现行资产价格低于执行价格时，其内在价值为执行价格减去现行价格（\(X-S_0\)）。如果资产的现行市价等于或高于执行价格，看跌期权的内在价值等于0。例如，看跌期权的执行价格为100元，现行价格为80元，其内在价值为20元（100-80)。如果现行价格变为120元，则内在价值为0。

由于标的资产的价格是随时间变化的，所以内在价值也是变化的。当执行期权能给持有人带来正回报时，称该期权为“实值期权”，或者说它处于“实值状态” （溢价状态）；当执行期权将给持有人带来负回报时，称该期权为“虚值期权”，或者谠它处于“虚值状态” （折价状态）；当资产的现行市价等于执行价格时，称期'权为“平价期权”，或者说它处于“平价状态”。

对于看涨期权来说，标的资产现行市价高于执行价格时，该期权处于实值状态；当资产的现行市价低于执行价格时，该期权处于虚值状态。对于看跌期权来说，资产现行市价低于执行价格时，该期权处于“实值状态”；当资产的现行市价高于执行价格时，该期权处于“虚值状态”。

期权处于虚值状态或平价状态时不会被执行，只有处于实值状态才有可能被执行，但也不一定会被执行。

例如，20x2年4月3日，ABC公司股票的市场价格为79元。有1股看跌期权，执行价格为80元，20x2年6月到期，期权售价为4元，持有者可以在6月18日前的任意一天执行。如果持有人购买后立即执行，执行收入为1元（80-79)。期权发行时处于实值状态，或者说发行日是实值期权。此时，持有人并不会立即执行以获取1元收益，因为他拢掉了4元钱成本，马上换回1元钱，并不划算。持有人购买看跌期权是预料将来股价会下跌，因此他会等待。只有到期日的实值期权才肯定会被执行，此时已不能再等待。

2. 期权的时间溢价

详细介绍

\[时间溢价= 期权价值-内在价值 \]

例如，股票的现行价格为120元，看涨期权的执行价格为100元，期权价格为21元，则时间溢价为1元（21-20）。如果现行价格等于或小于100元，则21元全部是时间溢价。

期权的时间溢价是一种等待的价值。期权买方愿意支付超出内在价值的溢价，是寄希望于标的股票价格的变化可以增加期权的价值。很显然，对于美式期权在其他条件不变的情况下，离到期时间越远，股价波动的可能性越大，期权的时间溢价也就越大。如果已经到期，期权的价值（价格）就只剩下内在价值（时间溢价为0)，因为巳经不能再等待了。

期权处于虚值状态，仍然可以按正的价格售出，尽管其内在价值为0，但它还有时间溢价。在未来的一段时间里，如果价格上涨进入实值状态，投资者可以获得净收入；如果价格进一步下跌，也不会造成更多的损失，选择权为其提供了下跌保护。

时间溢价有时也称为期权的时间价值，但它和货币的时间价值是不同的概念。时间溢价是时间带来的波动的价值，是未来存在不确定性而产生的价值，不确定性越强，期权时间价值越大。而货币的时间价值是时间延续的价值，时间延续得越长，货币时间价值越大。

（二）影响期权价值的主要因素

影响期权价值的主要因素

以下变量对于期权价格的影响如表6-10所示。

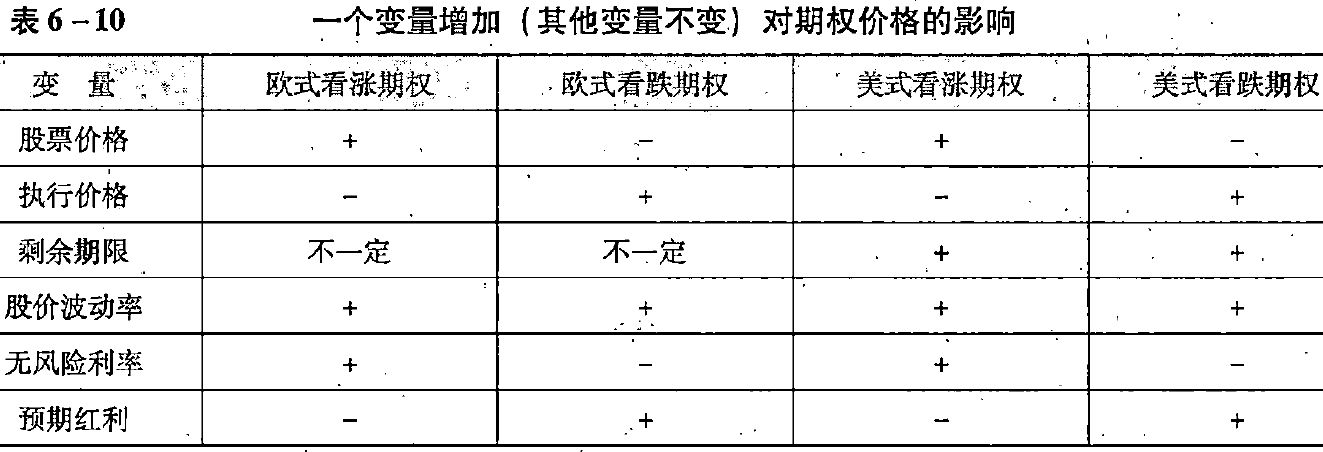
详细介绍

1. 股票市价

如果看涨期权在将来某一时间执行，其收入为股票价格与执行价格的差额。如果其他因素不变，随着股票市价的上升，看涨期权的价值也增加。看跌期权与看涨期权相反，看跌期权在未来某一时间执行其收入是执行价格与股票价格的差额。如果其他因素不变，当股票市价上升时，看跌期权的价值下降。

2. 执行价格

执行价格对期权价格的影响与股票市价相反。看涨期+又的执行价格越高，其价值越小。看跌期权的执行价格越高其价值越大。

3. 到期期限

对于美式期权来说，较长的到期时间能增加看涨期权的价值。到期日离现在越远，发生不可预知事件的可能性越大，股价变动的范围也越大。Jtfc外，随着时间的延长，执行价格的现值会减少，从而有利于看涨期权的持有人，能够增加期权的价值。
对于欧式期权来说，较长的时间不一定能增加期权价值。虽然较长的时间可以降低执行价格的现值，‘但并不增加执行的机会。到期日价格的降低:有可能超过时间价值的差额。例如，两个欧式看涨期权，一个是1个月后到期，另一个是3个月后到期，蓣计标的公司两个月后将发放大量现金股利股票价格会大幅下降，则有可能使时间长的期权价值低于时间短的期权价值。

4. 股价波动率

股价波动率，是指股票价格变动的不确定性，通常用标准差衡量。股票价格的波动率越大，股价上升或下降的机会越大。对于股票持有者来说，两种变动趋势可以相互抵消，期望股价是其均值。
对于看涨期权持有者来说，股价上升对其有利，股价下降对其不利，最大损失以期权费为限，两者不会抵消。因此，股价波动率增加会使看涨期权价值增加。对于看跌期权持有者来说股价下降对其有利，肢价上升对其不利，最大损失以期权费为限，两者不会抵消。因此，股价波动率增加会使看跌期权价值增加。
在期权估值过程中，股价的波动性是最重要的因素。如果一种股票的价格波动性很小，其期权也值不了多少钱。

5. 无风险利率

利率对于期权价格的影响是比较复杂的。
一种简单而不全面的解释是：假设股票价格不变，高利率会导致执行价格的现值降低，从而增加看涨期权的价值。
还有一种理解的办法是：投资于股票需要占用投资者一定的资金，投资于同样数量的该股票的看涨期权需要较少的资金。在高利率的情况下，购买股票并持有到期的成本越大，购买期权的吸引力越大。因此，无风险利率越高，看涨期权的价格越高。对于看跌期权来说，情况正好相反。

6. 预期红利

在除息日后，红利的发放引起股票价格降低，看涨期权价格降低。与此相反，股票价格的下降会引起看跌期权价格上升。因此，看跌期权价值与预期红利大小呈正向变动，而看涨期权价值与预期红利大小呈反向变动。

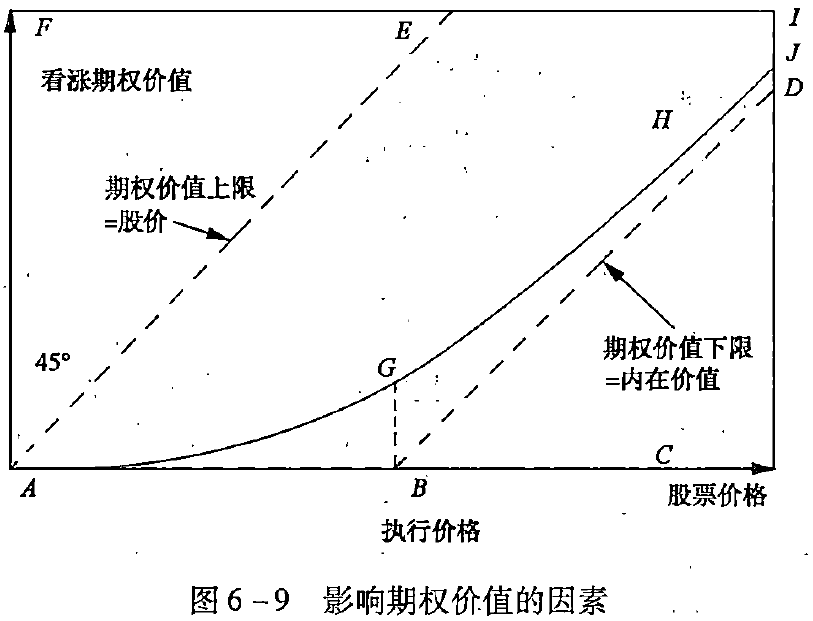
这些变量之间的关系如图6 - 9所示。

二、金融期权价值的评估方法★★

（一）期权估值原理

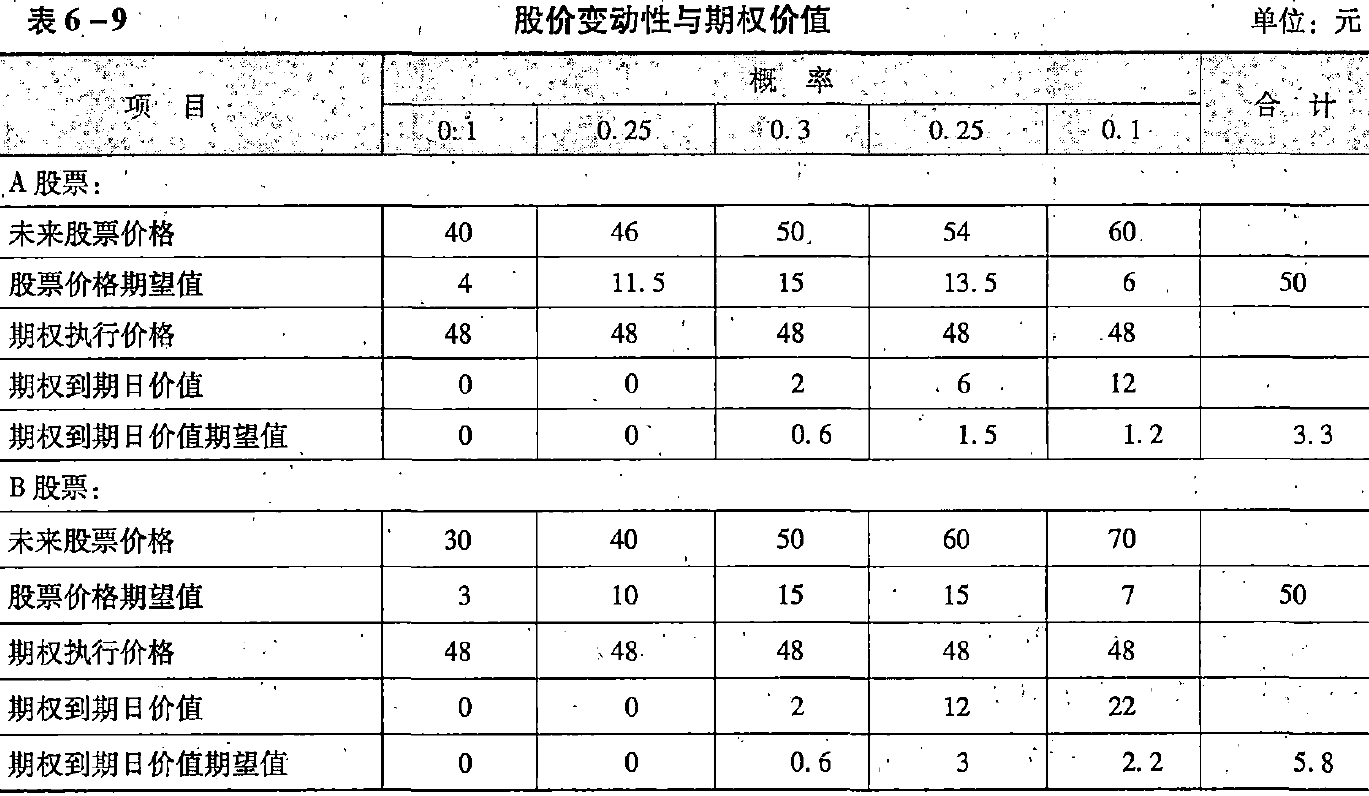
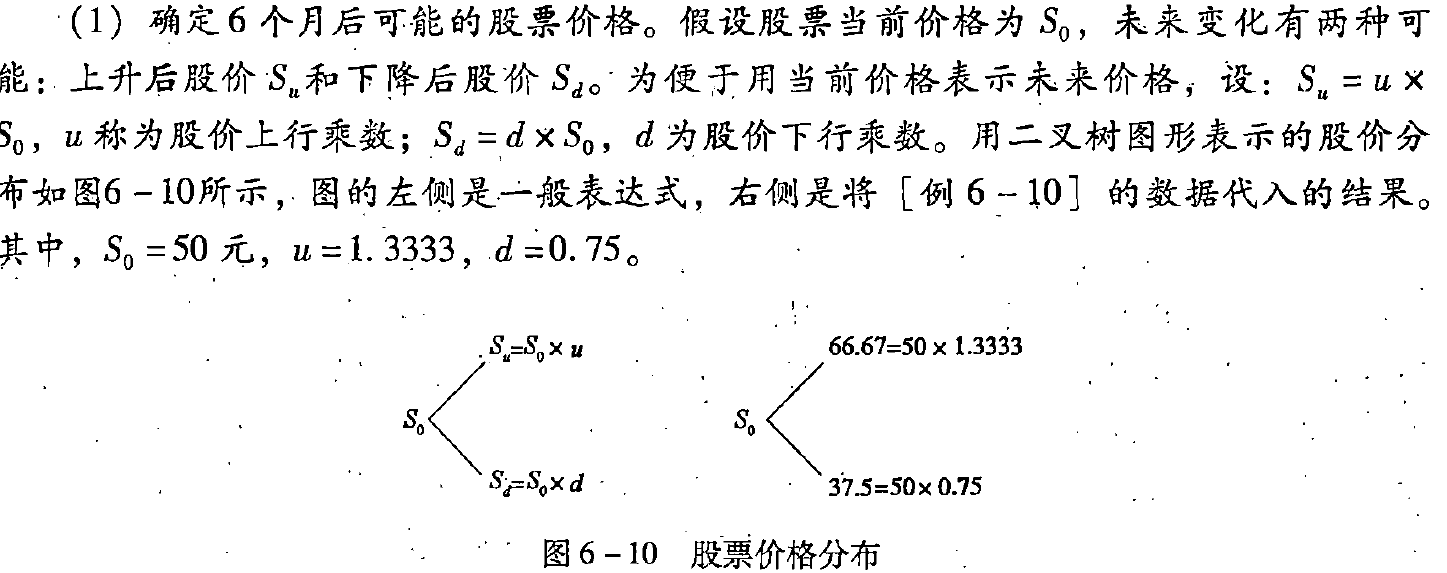
【例6-10】假设ABC公司的股票现在的市价为50元。有1股以该股票为标的资产的看涨期权，执行价格为52.08元，到期时间是6个月。6个月以后股价有两种可能：上升33.33%，或者下降25%，无风险利率为每年4%。拟建立一个投资组合，包括购进适量的股票以及借入必要的款项，使得该组合6个月后的价值与购进该看涨期权相等。

1. 复制原理

构造一个股票和借款的适当组合，使得无论股价如何变动，投资组合的损益都与期权相同，那么，创建该投资组合的成本就是期权的价值。

可以通过下列过程来确定该投资组合：

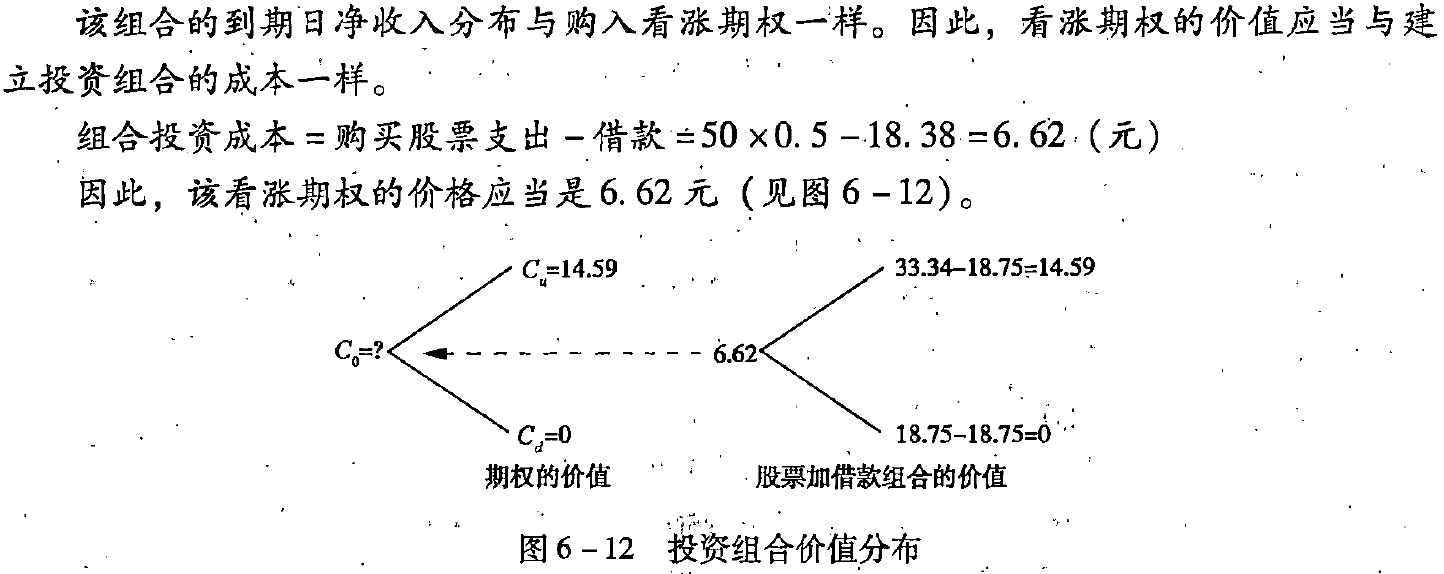
2. 套期保值原理

套期保值比率（套头比率、对冲比率、德尔塔系数）$H$

\[\begin{cases} S_u=S_0\times{u}\\ S_d=S_0\times{d}\\ C_u=max(S_u-X,0)\\ C_d=max(S_d-X,0)\\ \end{cases} \]

\[\begin{cases} S_u\times{H}+B\times(1+r)=C_u\\ S_d\times{H}+B\times(1+r)=C_d \end{cases} \]

==>

\[\begin{cases} H=\frac{C_u-C_d}{S_u-S_d}=\frac{C_u-C_d}{S_0\times(u-d)}\\ B=-\frac{S_d\times{H}-C_d}{(1+r)} \end{cases} \]

==>

\[C_0=S_0\times{H}+B \]

复制原理（套期保值）的解题过程

• （1）到期日的股票价格

\[\begin{cases} S_u=S_0\times{u} = 50{\times}1.3333 = 66.67(元)\\ S_d=S_0\times{d} = 50 {\times} 0.75 = 37.5(元) \end{cases} \]

• （2）到期日的期权价值

\[\begin{cases} C_u=max(S_u-X,0)=max(66.67-52.08,0)=14.59(元)\\ C_d=max(S_d-X,0)=max(37.50-52.08,0)=0 \end{cases} \]

• （3）套期保值比率

\[H=\frac{C_u-C_d}{S_u-S_d}=\frac{14.59-0}{66.67-37.5}=0.5 \]

• （4）投资组合的成本（期权价值）

\[\begin{split} 购买股票支出&=套期保值比率\times股票现价\\ &=0.5{\times}50 =25(元)\\ 借款&=\frac{S_d\times{H}-C_d}{1 + r}\\ &=\frac{37.5\times{0.5}-0}{l.02} = 18.38(元)\\ 期权价值C_0&=投资组合成本=购买股票支出-借款\\ &=25-18.38=6.62(元) \end{split} \]

3. 风险中性原理

假设投资者对待风险的态度是中性的，所有证券的预期报酬率都应当是无风险利率。风险中性的投资者不需要额外的收益补偿其承担的风险。在风险中性的世界里，将期望值用无风险利率折现，可以获得现金流量的现值。

所有证券的预期报酬率都应当是无风险利率，这个假设说明，CPA财务管理理论承认了：期权不创造价值，只转移价值。

计算过程

\[\begin{cases} S_u=S_0\times{u}\\ S_d=S_0\times{d}\\ C_u=max(S_u-X,0)\\ C_d=max(S_d-X,0)\\ \end{cases} \]

\[\begin{split} 期望报酬率&=上行概率p\times{上行时报酬率}+(1-p)\times{下行时报酬率}\\ 无风险利率r&=p\times{股价上升百分比(u-1)}+(1-p)\times{股价下降百分比(d-1)}\\ C_1&=p\times{C_u}+(1-p)\times{C_d}\\ C_0&=\frac{C_1}{1+r} \end{split} \]

（二）二叉树期权定价模型

1. 单期二叉树定价模型

详细介绍

• （1）二叉树模型的假设
  ①市场投资没有交易成本；
  ②投资者都是价格的接受者；
  ③允许完全使用卖空所得款项；
  ④允许以无风险利率借人或贷出款项；
  ⑤未来股票的价格将是两种可能值中的一个。

• （2）单期二叉树公式的推导
  应用上文期权估值的套期保值原理。
  

\[\begin{split} 初始投资&=股票投资-期权收入=S_0\times{H}-C_0\\ 投资到期曰终值&=(S_0\times{H}-C_0)\times(1+r)\\ 投资组合到期日价值&=S_0\times{H}\times{u}-C_u\\ 令{\quad}(S_0\times{H}-C_0)\times(1+r)&=S_0\times{H}\times{u}-C_u\\ 得{\quad}C_0\times{(1+r)}&=C_u\times\frac{(1+r)-d}{u-d}+C_d\times\frac{u-(1+r)}{u-d} \end{split} \]

2. 两期二叉树模型

由单期模型向两期模型的扩展，不过是单期模型的重复应用，任何一次应用均可使用上文的三种原理中的任何一个。

【例6-11】继续采用[例6-10]中的数据，把6个月的时间分为两期，每期3个月。变动以后的数据如下：ABC公司的股票现在的市价为50元看涨期权的执行价格为52.08元，每期股价有两种可能：上升22.56%或下降18.4%；无风险利率为每3个月1%。

答案

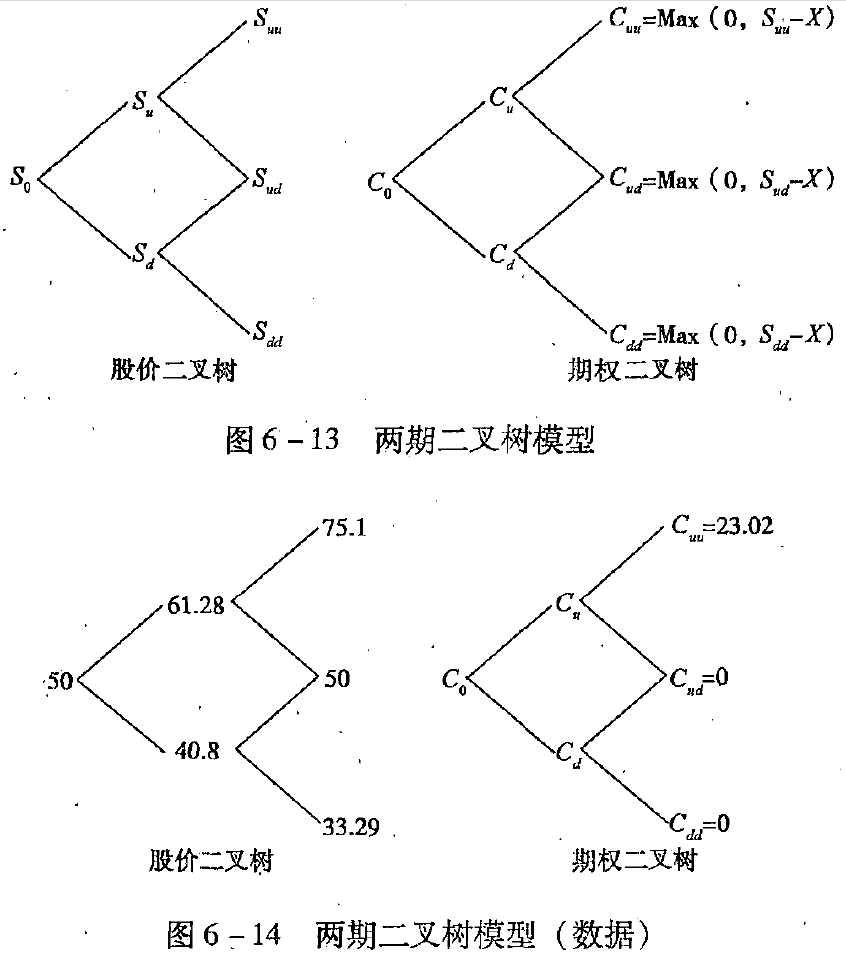
下面，分别以应用期权估值的复制原理和风险中性原理为例，解决两期二叉树模型下的期权估值问题。

• （1）应用复制原理

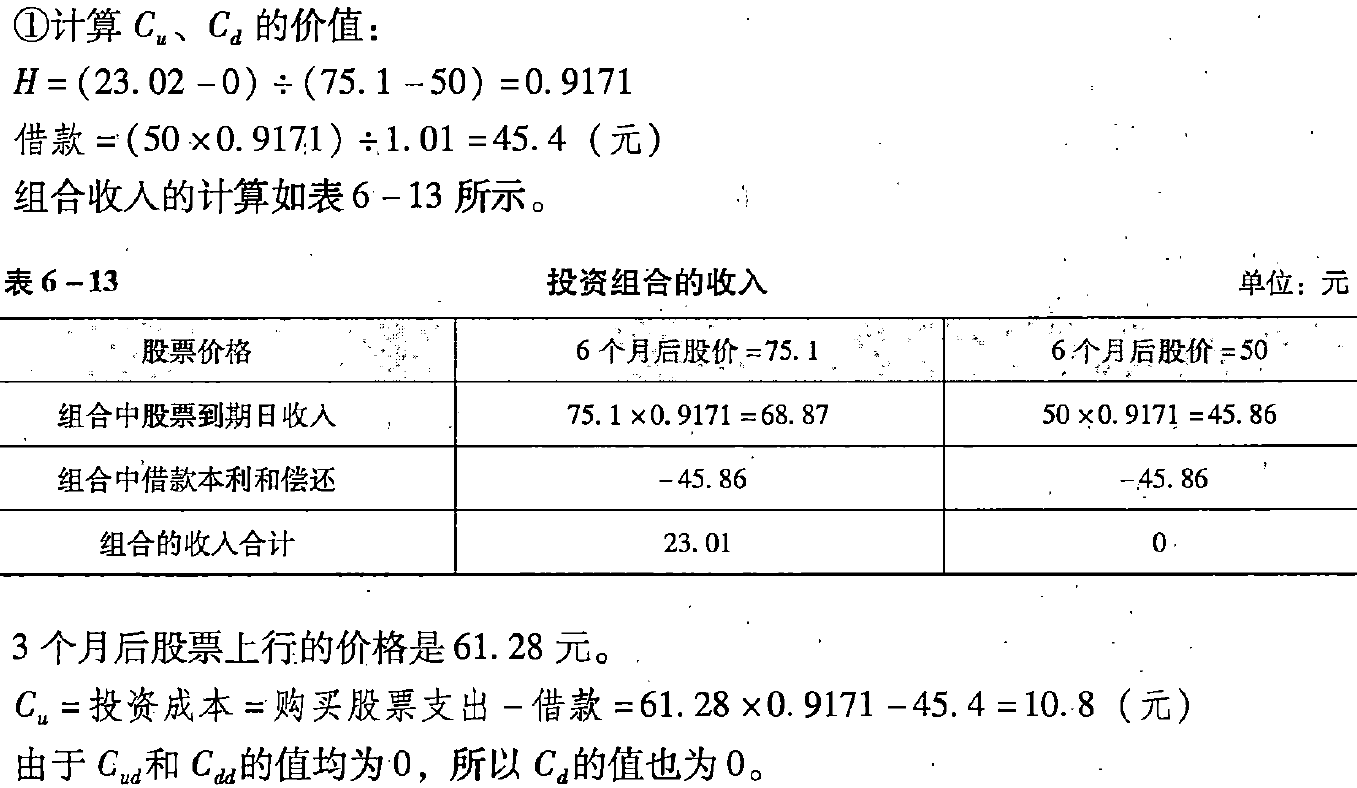
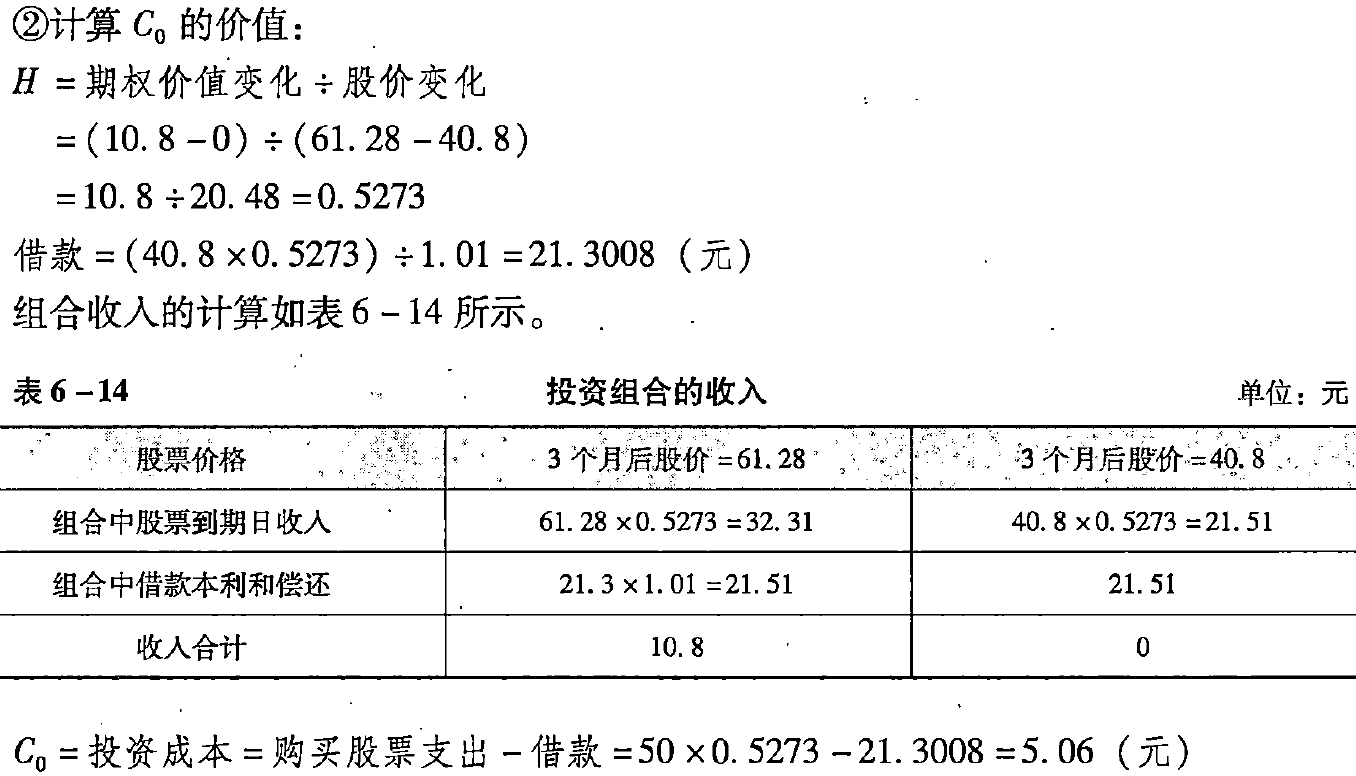
• （2）应用风险中性原理

综上，两期二叉树模型的公式推导过程如下：

两期二叉树模型的公式

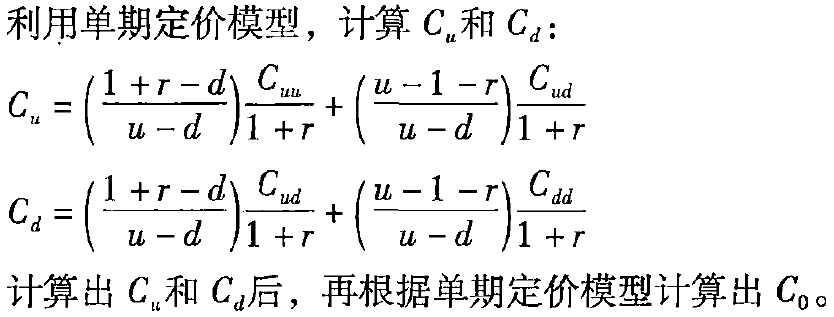
3. 多期二叉树模型

调整价格变化的升降幅度，以保证年报酬率的标准差不变。

年报酬率标准差和升降百分比联系起来

\[\begin{split} u&=1+上升百分比=e^{\sigma\times\sqrt{t}}\\ d&=1-下降百分比=\frac{1}{u} \end{split} \]

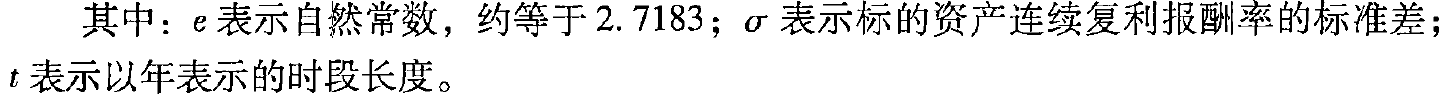
[例6 - 1 0 ]采用的标准差\(\sigma\)=0.4068。

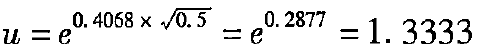
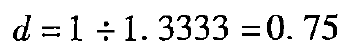
【例6-12】沿用[例6-10]中的数据，将半年的时间分为6期，即每月1期。已知：股票价格\(S_0\)=50元，执行价格为52.08元，年无风险利率为4%，股价波动率（标准差）为0.4068,到期时间为6个月，划分期数为6期（即每期1个月）。

答案

• （1）确定每期股价变动乘数
  

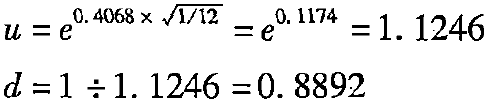
• （2）建立股票价格二叉树（见表6-15中的“股票价格” 部分）
  

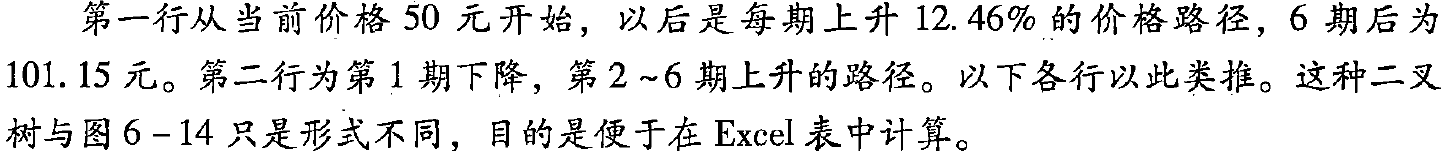
• （3）根据股票价格二叉树和执行价格，构建期权价值的二叉树（见表6-15中的“买入期权价格” 部分）。
  构建顺序为由后向前，逐级推进。
  
  
  

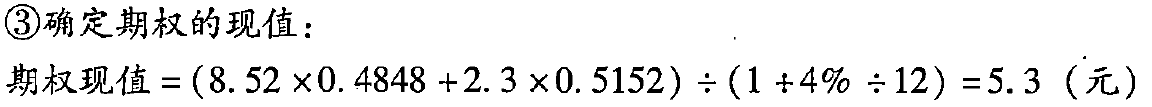
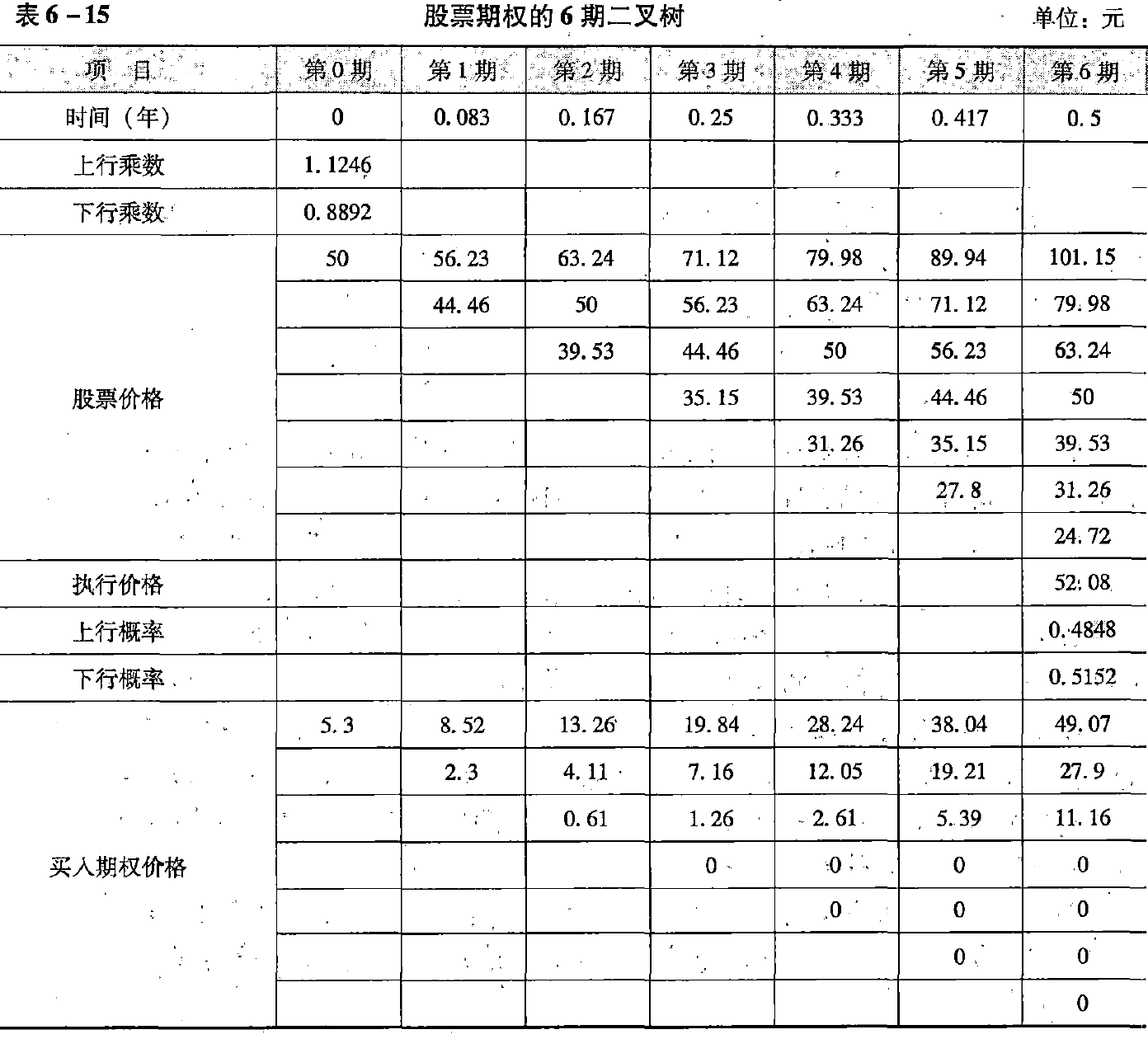
二叉树方法是一种近似的方法。不同的期数划分，可以得到不同的近似值。期数越多，计算结果与布莱克-斯科尔斯定价模型的计算结果差额越小。

（三）布莱克-斯科尔斯期权定价模（BS模型）

1. BS模型的假设

详细介绍

• （1）在期权寿命期内，期权标的股票不发放股利，也不做其他分配；

• （2）股票或期权的买卖没有交易成本；

• （3）短期的无风险利率是巳知的，并且在期权寿命期内保持不变；

• （4）任何证券购买者都能以短期的无风险利率借得任何数量的资金；

• （5）允许卖空，卖空者将立即得到所卖空股票当天价格的资金；

• （6）看涨期权只能在到期日执行；

• （7）所有证券交易都是连续发生的，股票价格随机游走。

2. BS模型公式

BS模型公式

\[\begin{split} {PV(X)}&=\frac{X}{e^{r_c\times{t}}}\\ {d_1}&=\frac{\ln(S_0/PV(X))}{\sigma\sqrt{t}}+\frac{\sigma\sqrt{t}}{2}\\ {d_2}&=d_1-\sigma\sqrt{t}\\ {C_0}&=S_0\times{N(d_1)}-PV(X)\times{N(d_2)} \end{split} \]

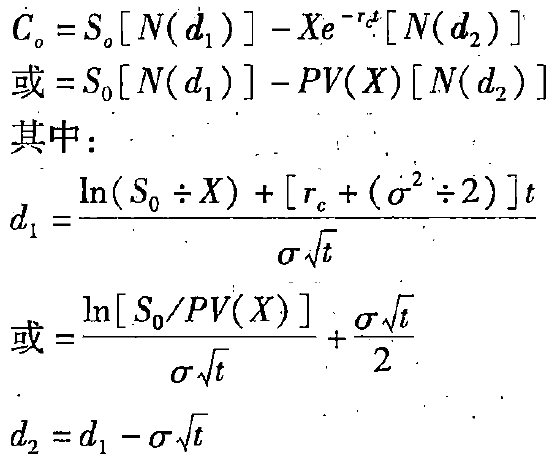
【例6-13】沿用[例6-10]的数据，某股票当前价格为50元，执行价格为52.08元，期权到期日前的时间为0.5年。每年复利一次的无风险利率为4%，相当连续复利的无风险利率\(r_c=\ln(1.04)=3.9221\%\)，连续复利的标准差\(\sigma=0.4068\)，即方差\(\sigma^2=0.16550\)。

答案

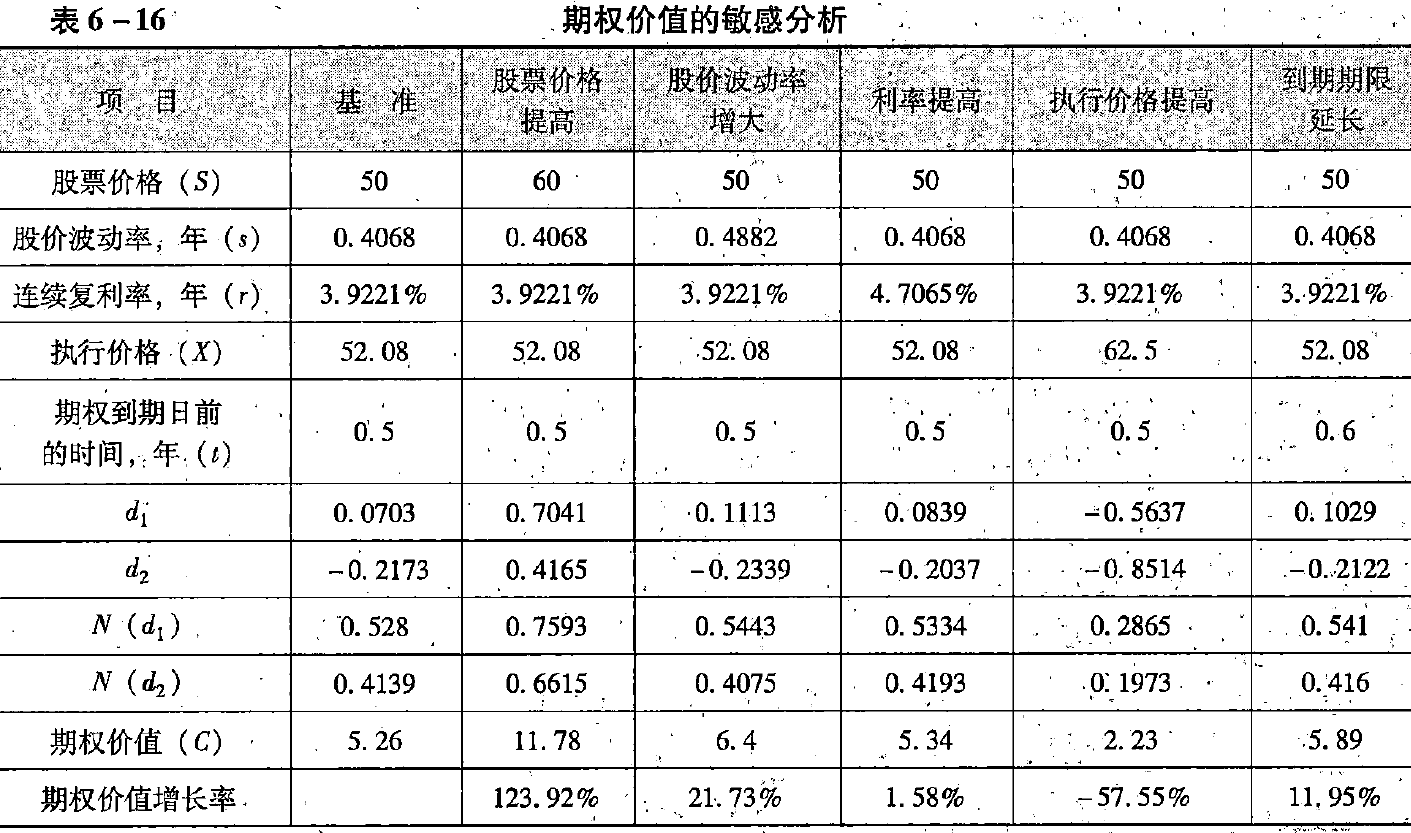
通过该模型可以看出，决定期权价值的因素有五个（股票价格、股价波动率、利率、执行价格和期权到期日前的时间）。它们对于期权价值的影响，可以通过敏感分析表来观察（见表6-16）。

3. 模型参数的估计

（1）无风险利率的估计

连续复利率

\[r_c=\frac{\ln{(F/P)}}{t} \]

【例6-14】假设t=1年，F=104元，P=100元，则：

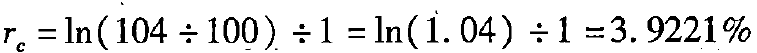
（2）报酬率标准差的估计

连续复利的股票报酬率

\[r_t=\ln(\frac{P_t+D_t}{P_{t-1}}) \]

连续复利标准差

\[\sigma=\sqrt{\frac{\sum_{t=1}^{n}{(r_t-\overline{r})^2}}{n-1}} \]

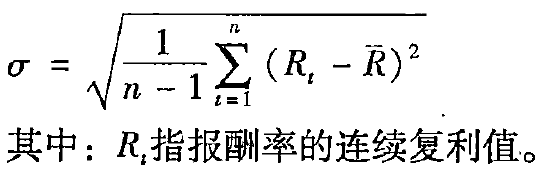
示例

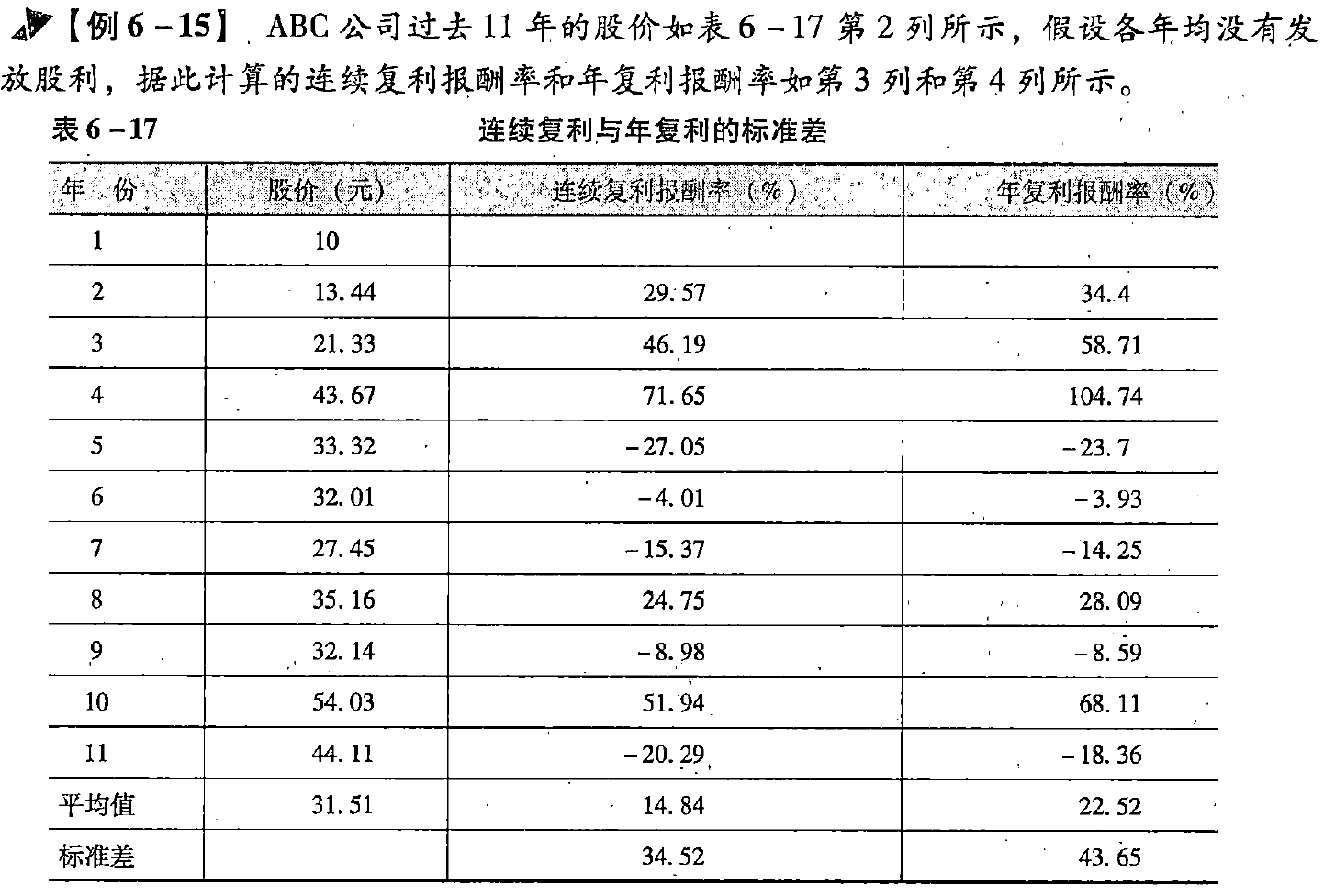
4. 看跌期权估值

欧式期权

看涨期权-看跌期权平价定理（关系）：

\[看涨期权C_0-看跌期权P_0=标的资产S_0-执行价格现值PV(X) \]

该公式的有效性，可以通过表6 - 18验证。

【例6-16】两种期权的执行价格均为30元，6个月到期，6个月的无风险利率为4%，股票的现行价格为35元，看涨期权的价格为9.2元，则看跌期权的价格为：

答案

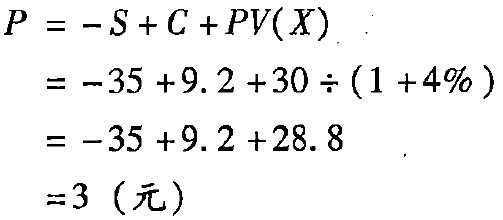
5. 派发股利的期权定价

考虑派发股利的期权定价公式

\[\begin{split} SS_0&=\frac{S_0}{e^{\delta{t}}}\\ PV(X)&=\frac{X}{e^{r_c\times{t}}}\\ d_1&=\frac{\ln(SS_0/PV(X))}{\sigma\sqrt{t}}+\frac{\sigma\sqrt{t}}{2}\\ d_2&=d_1-\sigma\sqrt{t}\\ C_0&=SS_0\times{N(d_1)}-PV(X)\times{N(d_2)} \end{split} \]

6. 美式期权估值

美式期权的价值应当至少等于相应欧式期权的价值，在某种情况下比欧式期权的价值更大。

End