动态DP学习笔记
动态DP学习笔记

约定:
- 若无特别说明,数组下标从1开始.
- 若无特别说明,矩阵的下标从0开始(这是为了和代码一致,而代码这样实现是为了节省内存)
- 在公式中,矩阵用粗斜体表示,如\(\bm{A}\)
- 若无特别说明,对于有根树上的结点\(x\),\(child(x)\)表示它儿子的集合,\(son(x)\)表示它的重儿子
- 对于实数的乘法,一律用\(+,\cdot\)表示,有字母时乘号可能省略。
可能需要的前置知识:
- 线段树
- DFS序,轻重链剖分
- LCT
- 矩阵乘法
问题引入
动态DP是指在动态规划问题中修改参量,并询问修改后的DP值。如果每次修改完之后都要朴素的重新DP一遍,时间复杂度很高,无法接受。
动态DP有很多解法。对于一些特殊动态DP问题,可以用离线处理,虚树,倍增等方法转化成普通的静态DP问题。这些方法虽然灵活方便且常数较小,但是可扩展性差。而本文讨论的是一种较为通用的解法,即把状态转移方程写成矩阵的形式,进而把修改操作转化为修改矩阵,查询操作转化为区间矩阵乘积,然后用数据结构维护矩阵。
序列上的动态DP
给出一个可能有负数序列\(a_i\),支持单点修改,区间查询最大子段和。即给出\([L,R]\),求$$\max_{L \leq l \leq r \leq R} \sum_{i=l}^{r}a_i$$
线段树维护包含左端点,包含右端点和区间内的答案显然可做。

如果查询整个序列的子段和,容易写出DP方程。设\(f_i\)表示以\(i\)结尾的最大子段和,显然有\(f_i=\max(f_{i-1}+a_i,a_i)\).但是这个方程无法快速修改和维护。
这时,我们想到了矩阵优化DP。
重新定义矩阵乘法
我们知道,一般的矩阵乘法可以写成$$c_{i,j}=\sum_{k=1}^m a_{i,k} \cdot b_{k,j}$$的形式。
我们知道,很多次加法可以变成乘法,那么什么运算可以变成加法?实际上是\(\max\)和\(\min\)运算。它们有类似的性质,比如:
\(\max(a,b)+c=\max(a+c,b+c)\)
$(a+b)\cdot c=a\cdot c+b \cdot c $.
那么我们可以重新定义矩阵乘法:
很(wo)容(bu)易(hui)证明这样的矩阵乘法满足结合律,不满足交换律
另外,容易发现在\(\max,+\)矩阵乘法中,\(-\infty\)充当了0的作用,0充当了1的作用,而单位矩阵是对角线为0,其他元素为\(-\infty\)的矩阵。在\(\min,+\)矩阵乘法中,则是\(+\infty\)
转化成数据结构问题
根据矩阵乘法的定义,我们可以写出如下的式子:
那么修改的时候就修改某个点对应的矩阵,查询的时候就是查询区间乘积。由于\(f_L\)的初始值为\(a_L\),我们可以直接查询\([L,R]\)的区间矩阵乘积\(\bm{S}\),然后输出\(\max(\bm{S_{0,0}},\bm{S_{1,0}})\)即可。
树上的动态DP
实际上,几乎没有在序列上的动态DP题目(如果有,一般也能用线段树等数据结构直接解决),大部分的动态DP题目都出现在树上。而树上的动态DP往往与链剖分紧密结合。
接下来我们讨论一个经典模型:树上最大权独立集。
LuoguP4719:给出一个\(n\)个点的树,每个点权值为\(v_i\),每次单点修改,查询整棵树的最大权独立集
设\(f_{x,0},f_{x,1}\)分别表示\(x\)子树中,不选择\(x\)的最大权独立集大小,和选择\(x\)的最大权独立集大小。显然有转移:
\(f_{x,0}=\sum_{y \in child(x)} \max(f_{y,0},f_{y,1})\)
\(f_{x,1}=\sum_{y \in child(x)} f_{y,0}\)
这个方程无法写成矩阵形式,考虑优化。
树链剖分+线段树解法
为了快速维护DP值,我们可以分轻重儿子维护DP值。
记
\(g_{x,0}=\sum_{y \in child(x)-\{son(x)\}} \max(f_{y,0},f_{y,1})\)
\(g_{x,1}=a_x+\sum_{y \in child(x)-\{son(x)\}} f_{y,0}\)
g维护了所有轻儿子的DP贡献,那么有:
\(f_{x,0}=\max(f_{son(x),0},f_{son(x),1})+g_{x,0}\)
\(f_{x,1}=f_{son(x),0}+g_{x,1}\)
写成矩阵的形式(注意这里是max,+矩阵乘法)
不妨将转移矩阵记为\(\bm{M_x}=\begin{bmatrix}g_{x,0} \ g_{x,0} \\ g_{x,1} \ -\infin \end{bmatrix}\)
因为\(x,son(x),son(son(x))\)构成的是一条重链,所以对于重链上的点,可以类似序列动态DP的方法,用查询区间\(\bm{M_x}\)乘积的方法求出它们的DP值,用线段树在DFS序上维护。
但是还要考虑对轻链的影响.
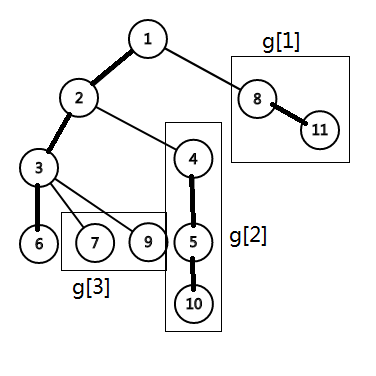
如图所示,从每个点的\(g\)的统计范围可以看出,每次修改只会影响\(x\)到根的路径上,每条重链的底端的\(g\)值.(\(x\)所在一条除外)。比如修改5会影响到2.于是我们先修改\(g_{x,1}\)(即\(\bm{{M_x}_{1,0}}\)),把它加上\(a_{x}\)的增加量,因为它的定义里包含\(a_x\).
然后沿着重链往上跳:
对于每条重链的链顶,我们要减去原来的\(f\)对链顶父亲的影响。还要求出这条重链上新的DP值,显然只需要考虑重链底端的影响,它轻儿子已经修改完了,我们根据新的\(g\)重新赋值\(\bm{M_x}\)矩阵,然后在线段树上单点修改。接着跳到链顶,在线段树上查询f值,然后更新链顶的父亲。
ll get_f(int x,int k) {
//f[x]需要从x所在重链底端推上来,变成区间矩阵乘法
return T.query(dfn[x],dfn[btm[x]],1).a[k][0];//btm[x]表示x所在重链的底端
}
void change(int x,int v) {
g[x][1]+=v-val[x];//先修改x
val[x]=v;
while(x) {
//对于重链底端,根据新的g重新赋值M[x]
mat[x].a[0][0]=g[x][0];
mat[x].a[0][1]=g[x][0];
mat[x].a[1][0]=g[x][1];
mat[x].a[1][1]=-INF;
T.update(dfn[x],mat[x],1);//单点修改
x=top[x];//对于链顶,要更新它父亲的g
g[fa[x]][0]-=max(f[x][0],f[x][1]);//减去旧的f
g[fa[x]][1]-=f[x][0];
f[x][0]=get_f(x,0);
f[x][1]=get_f(x,1);
g[fa[x]][0]+=max(f[x][0],f[x][1]);//加上新的f
g[fa[x]][1]+=f[x][0];
x=fa[x];//跳到上一条重链
}
}
在更新的实现中,也可以不用\(f\)和\(g\)数组,可以直接修改\(\bm{M}\)里的对应位置,但是要注意先减去对父亲的影响再修改。还要注意区分\(\bm{M}\)和线段树节点里的矩阵,\(\bm{M}\)里存的是\(g\)值,而线段树节点里存的实际上是\(f\)值。
该做法的时间复杂度是\(O(n\log^2 n)\)(矩阵乘法的复杂度看作常数).
完整代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
#define maxn 200000
using namespace std;
typedef long long ll;
int n,m;
struct edge {
int from;
int to;
int next;
} E[maxn*2+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v) {
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
head[u]=esz;
}
int fa[maxn+5],son[maxn+5],sz[maxn+5],top[maxn+5],btm[maxn+5]/*所在重链最底端*/,dfn[maxn+5],hash_dfn[maxn+5];
void dfs1(int x,int f) {
sz[x]=1;
fa[x]=f;
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=f) {
dfs1(y,x);
sz[x]+=sz[y];
if(sz[y]>sz[son[x]]) son[x]=y;
}
}
}
int tim=0;
void dfs2(int x,int t) {
top[x]=t;
dfn[x]=++tim;
hash_dfn[dfn[x]]=x;
if(son[x]) {
dfs2(son[x],t);
btm[x]=btm[son[x]];//维护重链最底端节点
} else btm[x]=x;
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa[x]&&y!=son[x]) {
dfs2(y,y);
}
}
}
struct matrix {
ll a[2][2];
inline void set(int x) {
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) a[i][j]=x;
}
}
friend matrix operator * (matrix p,matrix q) {
matrix ans;
ans.set(-INF);
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) {
for(int k=0; k<2; k++) {
ans.a[i][j]=max(ans.a[i][j],p.a[i][k]+q.a[k][j]);
}
}
}
return ans;
}
} mat[maxn+5];
ll val[maxn+5];
ll f[maxn+5][2],g[maxn+5][2];
void dfs3(int x) {
f[x][0]=0;
f[x][1]=val[x];
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa[x]) {
dfs3(y);
f[x][0]+=max(f[y][0],f[y][1]);
f[x][1]+=f[y][0];
}
}
g[x][0]=0,g[x][1]=val[x];
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa[x]&&y!=son[x]) {
g[x][0]+=max(f[y][0],f[y][1]);
g[x][1]+=f[y][0];
}
}
mat[x].a[0][0]=g[x][0];
mat[x].a[0][1]=g[x][0];
mat[x].a[1][0]=g[x][1];
mat[x].a[1][1]=-INF;
}
struct segment_tree {
struct node {
int l;
int r;
matrix v;
} tree[maxn*4+5];
void push_up(int pos) {
tree[pos].v=tree[pos<<1].v*tree[pos<<1|1].v;
}
void build(int l,int r,int pos) {
tree[pos].l=l;
tree[pos].r=r;
if(l==r) {
tree[pos].v=mat[hash_dfn[l]];
return;
}
int mid=(l+r)>>1;
build(l,mid,pos<<1);
build(mid+1,r,pos<<1|1);
push_up(pos);
}
void update(int upos,matrix &uval,int pos) {
if(tree[pos].l==tree[pos].r) {
tree[pos].v=uval;
return;
}
int mid=(tree[pos].l+tree[pos].r)>>1;
if(upos<=mid) update(upos,uval,pos<<1);
else update(upos,uval,pos<<1|1);
push_up(pos);
}
matrix query(int L,int R,int pos) {
if(L<=tree[pos].l&&R>=tree[pos].r) return tree[pos].v;
int mid=(tree[pos].l+tree[pos].r)>>1;
matrix ans;
ans.a[0][0]=ans.a[1][1]=0;
ans.a[0][1]=ans.a[1][0]=-INF;
if(L<=mid) ans=ans*query(L,R,pos<<1);
if(R>mid) ans=ans*query(L,R,pos<<1|1);
return ans;
}
} T;
ll get_f(int x,int k) {
//f[x]需要从x所在重链底端推上来,变成区间矩阵乘法
return T.query(dfn[x],dfn[btm[x]],1).a[k][0];
}
void change(int x,int v) {
g[x][1]+=v-val[x];
val[x]=v;
while(x) {
mat[x].a[0][0]=g[x][0];
mat[x].a[0][1]=g[x][0];
mat[x].a[1][0]=g[x][1];
mat[x].a[1][1]=-INF;
T.update(dfn[x],mat[x],1);
x=top[x];
g[fa[x]][0]-=max(f[x][0],f[x][1]);
g[fa[x]][1]-=f[x][0];
f[x][0]=get_f(x,0);
f[x][1]=get_f(x,1);
g[fa[x]][0]+=max(f[x][0],f[x][1]);
g[fa[x]][1]+=f[x][0];
x=fa[x];
}
}
int main() {
int u,v;
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++) scanf("%lld",&val[i]);
for(int i=1; i<n; i++) {
scanf("%d %d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
dfs1(1,0);
dfs2(1,1);
dfs3(1);
T.build(1,n,1);
for(int i=1; i<=m; i++) {
scanf("%d %d",&u,&v);
change(u,v);
printf("%lld\n",max(get_f(1,0),get_f(1,1)));
}
}
LCT解法
既然轻重链剖分可做,那么LCT也可做,只需要在Splay节点里维护子树矩阵乘积。把实链看成重链,虚链看成轻链即可。\(g\)维护的就是所有虚儿子的信息。初始的时候所有边都是虚边,fa指向原树上的父亲。
查询的时候直接splay(1),然后输出矩阵信息即可。
修改的时候要先access再splay.实际上的修改操作在access中完成。考虑access的过程
void access(int x){
for(int y=0;x;y=x,x=fa(x)){
splay(x);
rson(x)=y;
push_up(x);
}
}
rson(x)=y,实际上就是原来的rson(x)变成了轻儿子,y变成了重儿子。因此\(g\)要加上\(f_{rson(x)}\),去掉\(f_y\)。这个过程和LCT维护子树信息是类似的。
void access(int x) {
//这里和树剖向上跳重链更新是类似的
for(int y=0; x; y=x,x=fa(x)) {
splay(x);
//原来的rson(x)由实变虚
if(rson(x)){
mat[x].a[0][0]+=max(tree[rson(x)].v.a[0][0],tree[rson(x)].v.a[1][0]);
mat[x].a[1][0]+=tree[rson(x)].v.a[0][0];
//这里也可以不用f和g,直接写对应矩阵里的值
}
rson(x)=y;
if(rson(x)){
mat[x].a[0][0]-=max(tree[rson(x)].v.a[0][0],tree[rson(x)].v.a[1][0]);
mat[x].a[1][0]-=tree[rson(x)].v.a[0][0];
}
mat[x].a[0][1]=mat[x].a[0][0];
push_up(x);
}
}
时间复杂度是\(O(n\log n)\).由于树的形态不变,不需要make_root操作,也就不需要翻转标记和push_down.因此动态DP中的LCT的常数并没有那么大,很多时候跑的比树剖快。
完整代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
#define maxn 200000
using namespace std;
typedef long long ll;
int n,m;
struct edge {
int from;
int to;
int next;
} E[maxn*2+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v) {
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
head[u]=esz;
}
struct matrix {
ll a[2][2];
matrix(){
a[0][0]=a[0][1]=a[1][0]=a[1][1]=-INF;
}
inline void set(int x) {
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) a[i][j]=x;
}
}
friend matrix operator * (matrix p,matrix q) {
matrix ans;
ans.set(-INF);
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) {
for(int k=0; k<2; k++) {
ans.a[i][j]=max(ans.a[i][j],p.a[i][k]+q.a[k][j]);
}
}
}
return ans;
}
} mat[maxn+5];
ll val[maxn+5];
ll f[maxn+5][2],g[maxn+5][2];
struct LCT {
#define lson(x) (tree[x].ch[0])
#define rson(x) (tree[x].ch[1])
#define fa(x) (tree[x].fa)
struct node {
int ch[2];
int fa;
matrix v;
} tree[maxn+5];
inline bool is_root(int x) { //注意合并顺序
return !(lson(fa(x))==x||rson(fa(x))==x);
}
inline int check(int x) {
return rson(fa(x))==x;
}
void push_up(int x) {
tree[x].v=mat[x];
if(lson(x)) tree[x].v=tree[lson(x)].v*tree[x].v;
if(rson(x)) tree[x].v=tree[x].v*tree[rson(x)].v;
}
void rotate(int x) {
int y=tree[x].fa,z=tree[y].fa,k=check(x),w=tree[x].ch[k^1];
tree[y].ch[k]=w;
tree[w].fa=y;
if(!is_root(y)) tree[z].ch[check(y)]=x;
tree[x].fa=z;
tree[x].ch[k^1]=y;
tree[y].fa=x;
push_up(y);
push_up(x);
}
void splay(int x) {
while(!is_root(x)) {
int y=fa(x);
if(!is_root(y)) {
if(check(x)==check(y)) rotate(y);
else rotate(x);
}
rotate(x);
}
}
void access(int x) {
//access的时候可能由实变虚,或由虚变实,因此要更新f,g,方法类似LCT维护虚子树信息
//这里和树剖向上跳重链更新是类似的
for(int y=0; x; y=x,x=fa(x)) {
splay(x);
//原来的rson(x)由实变虚
if(rson(x)){
mat[x].a[0][0]+=max(tree[rson(x)].v.a[0][0],tree[rson(x)].v.a[1][0]);//这里也可以不用f和g,直接写对应矩阵里的值
mat[x].a[1][0]+=tree[rson(x)].v.a[0][0];
}
rson(x)=y;
if(rson(x)){
mat[x].a[0][0]-=max(tree[rson(x)].v.a[0][0],tree[rson(x)].v.a[1][0]);
mat[x].a[1][0]-=tree[rson(x)].v.a[0][0];
}
mat[x].a[0][1]=mat[x].a[0][0];
push_up(x);
}
}
void change(int x,int v) {
access(x);
splay(x);
mat[x].a[1][0]+=v-val[x];
push_up(x);
val[x]=v;
}
ll query(int x) {
splay(1);//查询前记得splay到根
return max(tree[1].v.a[0][0],tree[1].v.a[1][0]);
}
} T;
void dfs(int x,int fa) {
f[x][0]=0;
f[x][1]=val[x];
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa) {
dfs(y,x);
f[x][0]+=max(f[y][0],f[y][1]);
f[x][1]+=f[y][0];
}
}
mat[x].a[0][0]=mat[x].a[0][1]=f[x][0];//一开始全是轻边,f=g
mat[x].a[1][0]=f[x][1];
mat[x].a[1][1]=-INF;
T.tree[x].v=mat[x];//初始化LCT
T.tree[x].fa=fa; //记得初始化fa
}
int main() {
int u,v;
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++) scanf("%lld",&val[i]);
for(int i=1; i<n; i++) {
scanf("%d %d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
dfs(1,0);
for(int i=1; i<=m; i++) {
scanf("%d %d",&u,&v);
T.change(u,v);
printf("%lld\n",T.query(1));
}
}
全局平衡二叉树解法
我们在前面提到,动态DP的树剖+线段树解法和LCT解法的常数都不是很优秀。全局平衡二叉树解法很小,且实现简洁。
全局平衡二叉树,实际上结合了LCT和树剖的特点。它的结构类似一棵静态的LCT,但修改方法又类似树剖。
在LCT中,一开始所有边都是虚边,那么初次access的复杂度可能就是\(O(n)\)了,虽然均摊的总复杂度是正确的,但常数不是很优秀。因此我们不妨用树剖的思路,初始时就对轻重边进行划分之后不再改变,并且划分方法要保证暴力向上跳的复杂度尽量小。
我们知道,在LCT里每棵Splay维护的是原树中的一条链。在全局平衡二叉树中,每棵平衡二叉树(BST)维护的是一条重链的全部节点,BST之间用fa指针链接,BST根的fa指向这条重链顶端的父亲所在重链,那么暴力沿着fa指针往上跳,对于每个根节点进行\(g\)的修改即可。为了让树高为\(O(\log n)\)级别以保证跳重链的复杂度,我们要找到重链按轻子树大小的带权重心,把它作为根,然后递归向下对两边重链建BST,分别设为左右儿子。
//stk[l,r]里存储当前重链的全部节点
//sumsz存储轻子树大小的前缀和
int get_bst(int l,int r) {
if(l>r) return 0;
int mid=lower_bound(sumsz+l,sumsz+r+1,(sumsz[l-1]+sumsz[r])/2)-sumsz;//求带权重心
int x=stk[mid];
lson(x)=get_bst(l,mid-1);
rson(x)=get_bst(mid+1,r);//递归建树,这样的二叉树是平衡的
if(lson(x)) fa(lson(x))=x;//类似LCT,初始化fa和son
if(rson(x)) fa(rson(x))=x;
push_up(x);
return x;
}
建树的过程同样可以通过DFS实现,我们先递归重儿子,得到整条重链,然后调用get_bst()对它建出BST.
int build(int x,int f) {
int rt=0;
stk[++tot]=x;
sumsz[tot]+=lsz[x];
if(son[x]) { //继续dfs重链
sumsz[tot+1]+=sumsz[tot];
rt=build(son[x],x);
} else { //到了重链底部,可以建二叉树了
rt=get_bst(1,tot);
for(int i=1; i<=tot; i++) sumsz[i]=0;
tot=0;
return rt;
}
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=f&&y!=son[x]) fa(build(y,x))=x;//对于轻链,递归下去建树,再用fa把它们连起来
}
return rt;
}
修改操作很简单,直接沿着fa暴力跳,只有到了每棵BST的根时才需要修改。这里相当于树剖时跳到重链顶端的操作。
void update(int x) {
while(x) { //这一部分和树剖跳重链类似
int f=fa(x);
if(f&&is_root(x)) {//只有到了BST根的时候,说明已经处理完了整条重链,跳轻链到fa(x)更新上一条重链
//删掉原来的f的影响
mat[f][0][0]-=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][0][1]-=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][1][0]-=tree[x].v[0][0];
}
push_up(x);
if(f&&is_root(x)) {
//更新现在的f的影响
mat[f][0][0]+=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][0][1]+=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][1][0]+=tree[x].v[0][0];
}
x=fa(x);
}
}
查询操作直接输出根节点的矩阵值即可。
时间复杂度\(O(n\log n)\),且常数很小。
完整代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#define INF 0x3f3f3f3f
#define maxn 200000
using namespace std;
typedef long long ll;
int n,m;
struct edge {
int from;
int to;
int next;
} E[maxn*2+5];
int head[maxn+5];
int esz=1;
void add_edge(int u,int v) {
esz++;
E[esz].from=u;
E[esz].to=v;
E[esz].next=head[u];
head[u]=esz;
}
struct matrix {
ll a[2][2];
matrix() {
a[0][0]=a[0][1]=a[1][0]=a[1][1]=-INF;
}
inline void set(int x) {
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) a[i][j]=x;
}
}
friend matrix operator * (matrix p,matrix q) {
matrix ans;
ans.set(-INF);
for(int i=0; i<2; i++) {
for(int j=0; j<2; j++) {
for(int k=0; k<2; k++) {
ans.a[i][j]=max(ans.a[i][j],p.a[i][k]+q.a[k][j]);
}
}
}
return ans;
}
ll* operator [](int i) {
return a[i];
}
} mat[maxn+5];
ll val[maxn+5];
ll f[maxn+5][2],g[maxn+5][2];
int sz[maxn+5],lsz[maxn+5],son[maxn+5];
void dfs1(int x,int fa) {
sz[x]=lsz[x]=1;
f[x][0]=0;
f[x][1]=val[x];
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa) {
dfs1(y,x);
f[x][0]+=max(f[y][0],f[y][1]);
f[x][1]+=f[y][0];
sz[x]+=sz[y];
if(sz[son[x]]<sz[y]) son[x]=y;
}
}
g[x][0]=0,g[x][1]=val[x];
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=fa&&y!=son[x]) {
g[x][0]+=max(f[y][0],f[y][1]);
g[x][1]+=f[y][0];
lsz[x]+=sz[y];
}
}
mat[x].a[0][0]=g[x][0];
mat[x].a[0][1]=g[x][0];
mat[x].a[1][0]=g[x][1];
mat[x].a[1][1]=-INF;
}
struct BST {
#define fa(x) (tree[x].fa)
#define lson(x) (tree[x].ch[0])
#define rson(x) (tree[x].ch[1])
int root;
int tot;
int stk[maxn+5];//存储当前重链
int sumsz[maxn+5];//存储重链上点的lsz之和
struct node {
int fa;//全局平衡二叉树上的父亲
int ch[2];
matrix v;
} tree[maxn+5];
inline bool is_root(int x) { //注意合并顺序
return !(lson(fa(x))==x||rson(fa(x))==x);
}
void push_up(int x) {//很多函数和LCT是一样的
tree[x].v=mat[x];
if(lson(x)) tree[x].v=tree[lson(x)].v*tree[x].v;
if(rson(x)) tree[x].v=tree[x].v*tree[rson(x)].v;
}
int get_bst(int l,int r) {
if(l>r) return 0;
int mid=lower_bound(sumsz+l,sumsz+r+1,(sumsz[l-1]+sumsz[r])/2)-sumsz;//求带权重心
int x=stk[mid];
lson(x)=get_bst(l,mid-1);
rson(x)=get_bst(mid+1,r);//递归建树,这样的二叉树是平衡的
if(lson(x)) fa(lson(x))=x;//类似LCT,初始化fa和son
if(rson(x)) fa(rson(x))=x;
push_up(x);
return x;
}
int build(int x,int f) {
int rt=0;
stk[++tot]=x;
sumsz[tot]+=lsz[x];
if(son[x]) { //继续dfs重链
sumsz[tot+1]+=sumsz[tot];
rt=build(son[x],x);
} else { //到了重链底部,可以建二叉树了
rt=get_bst(1,tot);
for(int i=1; i<=tot; i++) sumsz[i]=0;
tot=0;
return rt;
}
for(int i=head[x]; i; i=E[i].next) {
int y=E[i].to;
if(y!=f&&y!=son[x]) fa(build(y,x))=x;//对于轻链,递归下去建树,再用fa把它们连起来
}
return rt;
}
void update(int x) {
while(x) { //这一部分和树剖跳重链类似
int f=fa(x);
if(f&&is_root(x)) {//只有到了BST根的时候,说明已经处理完了整条重链,跳轻链到fa(x)更新上一条重链
mat[f][0][0]-=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][0][1]-=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][1][0]-=tree[x].v[0][0];
}
push_up(x);
if(f&&is_root(x)) {
mat[f][0][0]+=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][0][1]+=max(tree[x].v[0][0],tree[x].v[1][0]);
mat[f][1][0]+=tree[x].v[0][0];
}
x=fa(x);
}
}
void ini(){
dfs1(1,0);
root=build(1,0);
}
void change(int x,int v) {
mat[x][1][0]+=v-val[x];
val[x]=v;
update(x);
}
ll query(){
return max(tree[root].v[0][0],tree[root].v[1][0]);
}
} T;
int main() {
int u,v;
scanf("%d %d",&n,&m);
for(int i=1; i<=n; i++) scanf("%lld",&val[i]);
for(int i=1; i<n; i++) {
scanf("%d %d",&u,&v);
add_edge(u,v);
add_edge(v,u);
}
T.ini();
// T.debug();
for(int i=1; i<=m; i++) {
scanf("%d %d",&u,&v);
T.change(u,v);
printf("%lld\n",T.query());
}
}
例题
[NOIP2018]保卫王国
给出一棵\(n\)个点树,有m组询问,每次询问给出两个点,规定他们必须选或必须不选。求树的最小权覆盖集。\(n,m \leq 10^5\)
此题有倍增+树形dp的做法,常数非常优秀,但思路比较难想到。
显然最小权覆盖集=总点权和-最大权独立集
看到最大权独立集,可以直接套上面的模板
考虑如何处理询问。由于我们要权值最小,如果必须选某个点,就把它的点权修改为\(-\infty\),如果必须不选,就修改为\(+\infty\).代码实现上就把它修改成大于所有点权值之和的数即可,如\(10^{10}\).然后用板子求最大权独立集,再用总和减去。注意当我们把点权修改为\(-\infty\)时,最小权覆盖集会包含\(-\infty\),这时算出的和并不是真正答案,还要加上\(v_x-(-\infty)\),其中\(v_x\)是被强制选的值。
因为树剖和LCT两种实现动态DP的方式常数过大,没有O2的情况下会TLE,而众所周知NOIP是没有O2优化的。因此这里只给出全局平衡二叉树写法的代码。
为了节约篇幅,代码见这里
[LuoguP4426][AHOI2018]毒瘤
给出一个\(n\)个点\(m\)条边的无向图,求独立集个数。
\(n \leq 10^5,n-1 \leq m \leq n+10\)
注意到\(|m-n|\)很小,我们可以暴力枚举这些非树边\((u,v)\)的状态,按两边选和不选有(0,0)(0,1)(1,0)三种。其实可以合并为2种:
- \(u\)强制不选,\(v\)可任意选
- \(u\)强制选,\(v\)强制不选
那么直接暴力枚举每条边的状态,然后在树上修改,做动态DP即可。
设\(f_{x,0},f_{x,1}\)分别表示\(x\)不选/选,\(x\)子树中的独立集个数,那么:
\(f_{x,0}=1+\prod_{y \in child(x)} (f_{y,0}+f_{y,1})\)
\(f_{x,1}=1+\prod_{y \in child(x)} f_{y,0}\)
最终答案为\(f_{x,0}+f_{x,1}\)
记
\(g_{x,0}=1+\prod_{y \in child(x)-\{son(x)\}} (f_{y,0}+f_{y,1})\)
\(g_{x,1}=1+\prod_{y \in child(x)-\{son(x)\}} f_{y,0}\)
g维护了所有轻儿子的DP贡献,那么有:
\(f_{x,0}=(f_{son(x),0}+f_{son(x),1})\cdot g_{x,0}\)
\(f_{x,1}=f_{son(x),0} \cdot g_{x,1}\)
写成矩阵的形式(注意这里是+,\(\cdot\)矩阵乘法)
记\(\bm{M_x}=\begin{bmatrix}g_{x,0} \ g_{x,0} \\ g_{x,1} \ 0 \end{bmatrix}\)。为了处理强制选和不选的情况,我们还需要对每个节点定义一个矩阵\(\bm{C_x}\),求区间矩阵积的时候把乘\(\bm{M_x}\)变成乘\(\bm{C_xM_x}\)
注意到\(\begin{bmatrix} 0 \ 0 \\ 0 \ 1\end{bmatrix}\begin{bmatrix}f_{x,0} \\ f_{x,1} \end{bmatrix}=\begin{bmatrix}0 \\ f_{x,1} \end{bmatrix}\),于是使得\(f_{x,0}=0\),那么\(\bm{C_x}=\begin{bmatrix} 0 \ 0 \\ 0 \ 1\end{bmatrix}\)就表示强制选\(x\).同理\(\bm{C_x}=\begin{bmatrix} 1 \ 0 \\ 0 \ 0\end{bmatrix}\)就表示强制不选\(x\),\(\bm{C_x}=\begin{bmatrix} 1 \ 0 \\ 0 \ 1\end{bmatrix}\)就表示选和不选\(x\)均可。于是枚举的时候单点修改即可。
但是还有一个问题,在动态DP的过程中,我们需要把儿子的影响从父亲中消除,也就是说要做除法。但是万一\(f_y=0\),就会出现除0的问题。于是我们可以对于每个\(f\)和\(g\)值,记录它们被乘进去了几个0,做除法的时候0的个数会减少。如果减到了0,就变成了它们的真实值。具体实现可以定义一个新的类,重载它的*,/运算符
struct mynum { //为了消除下方g对上方g的影响,要支持撤回乘0操作
ll val;
int cnt;//记录被乘上去的0个数
mynum() {
val=cnt=0;
}
mynum(ll _val) {
if(_val==0) val=cnt=1;
else val=_val,cnt=0;
}
friend mynum operator * (mynum p,mynum q) {
mynum ans;
ans.val=p.val*q.val%mod;//把0的val设为1,这样乘的时候val就不变
ans.cnt=p.cnt+q.cnt;
return ans;
}
friend mynum operator / (mynum p,mynum q) {
mynum ans;
ans.val=p.val*inv(q.val)%mod;
ans.cnt=p.cnt-q.cnt;
return ans;
}
ll value() {
if(cnt==0) return val;
else return 0;
}
};
用LCT实现,复杂度\(O(n+m+2^{m-n}\log n)\),常数还可以。
为了节约篇幅,代码见这里
总结
我们介绍了动态DP的通用解法:把DP方程写成矩阵形式,然后用矩阵乘法维护信息。然后又把它应用到树上,和轻重链剖分,LCT与全局平衡二叉树结合。值得注意的是,动态DP有常数较大和代码量较大的缺点,对于许多题目,实际上可以不用这种通用解法解决,而是有更灵活的解法,需要结合实际问题分析。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号