[Codeforces1036E]Covered Points(计算几何求线段交点)
[Codeforces1036E]Covered Points(计算几何求线段交点)
题面
给出\(n\)条起点和终点都是整点的线段,问这些线段能够覆盖多少个整点.保证线段两两不共线
\(n \leq 1000\)
分析
先不考虑线段相交的情况,只考虑一条线段\(AB\)上有多少个整点.设\(\vec{u}=\vec{AB}\),那么答案就是\(\gcd(|\vec{u}_x|,|\vec{u}_y|)\)
线段的交点会被重复算,因此考虑计算线段的交点被多少条线段覆盖,把重复算的减掉.我们两两计算线段交点,用一个map记录整交点出现的次数,如果点\(P\)出现了\(a\)次,即有\(a\)对线段交点为\(P\),因此线段个数\(x\)满足\(\frac{x(x-1)}{2}=a\),解得\(x=\frac{1+\sqrt{1+8a}}{2}\). 那么就从答案中减去\(x-1\)即可
如何判断线段相交和求交点呢,可以用直线两点式爆算。但是有很优美的向量解法,且没有精度误差。
线段相交的判断
快速排斥实验:
以线段\(AB\)和\(CD\)为对角线做矩形,如果这两个矩形不相交,那么这两条线段也一定不相交
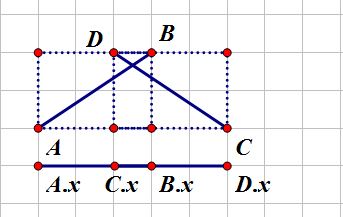
(点的标号有点问题,但是应该能看出来)
把线段投影到\(x\)轴上,那么显然有\(\max(A.x,B.x)\geq \min(C.x,D.x) 且 \max(C.x,D.x) \geq \min(A.x,B.x)\)
y轴同理
这个判断被称为快速排斥实验.但是矩形相交线段就一定相交吗?下面给出了一个反例
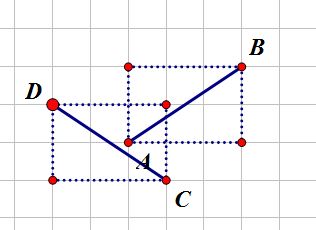
因此,我们还要用到跨立实验.
跨立实验:
如果点\(C,D\)在直线\(AB\)的不同侧,则称线段\(CD\)跨立直线\(AB\).两线段相交,当且仅当它通过快速排斥实验,且互相跨立。
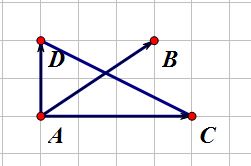
可以用叉积实现.根据叉积符号的定义知,\((\vec{AB} \times \vec{AD})(\vec{AB} \times \vec{AC})<0\)
bool is_cross(point A,point B,point C,point D){
if(max(A.x,B.x)>=min(C.x,D.x)&&max(C.x,D.x)>=min(A.x,B.x)&&max(A.y,B.y)>=min(C.y,D.y)&&max(C.y,D.y)>=min(A.y,B.y)){//快速排斥实验
//跨立实验
if(sgn(cross(C-A,B-A))*sgn(cross(D-A,B-A))<=0&&sgn(cross(A-C,D-C))*sgn(cross(B-C,D-C))<=0) return 1;//sgn(x)表示x的符号(-1,0,1),不要直接乘,防止溢出
else return 0;
}else return 0;
}
向量法求线段交点
如果上一步我们已经知道两线段相交,那么就可以利用叉积求交点。
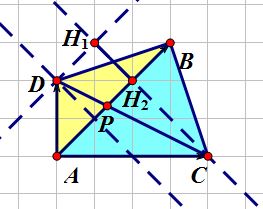
根据叉积的几何意义知道,\(S_{\Delta ADB}=\frac{1}{2}|\vec{AB} \times \vec{AD}|,S_{\Delta ACB}=\frac{1}{2}|\vec{AB} \times \vec{AC}|\)
做出三角形的高,显然\(\frac{CH_2}{H_1H_2}=\frac{S_{\Delta ACB}}{S_{\Delta ADB}}\)
根据相似三角形得\(\vec{CP}=\frac{CH_2}{H_1H_2+CH_2}\vec{CD}=\frac{|\vec{AB} \times \vec{AC}|}{|\vec{AB} \times \vec{AD}|+|\vec{AB} \times \vec{AC}|}\vec{CD}\)
\(\vec{CP}\)知道了,\(P\)的坐标也就知道了.
实现上还需要注意一个细节.容易发现除了最后一步的除法之外没有精度误差。那么判断整点只需要在最后一步判余数是否为0即可,不要强行除了之后再取整判断,否则会被卡精度
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#define maxn 1000
#define eps 1e-7
using namespace std;
typedef long long ll;
typedef long long ll;
ll gcd(ll a,ll b){
if(b==0) return a;
else return gcd(b,a%b);
}
struct Vector{
ll x;
ll y;
Vector(){
}
Vector(ll _x,ll _y){
x=_x;
y=_y;
}
friend Vector operator + (Vector p,Vector q){
return Vector(p.x+q.x,p.y+q.y);
}
friend Vector operator - (Vector p,Vector q){
return Vector(p.x-q.x,p.y-q.y);
}
friend Vector operator * (Vector p,ll k){
return Vector(p.x*k,p.y*k);
}
friend Vector operator / (Vector p,ll k){
return Vector(p.x/k,p.y/k);
}
};
typedef Vector point;
inline ll dot(Vector p,Vector q){
return p.x*q.x+p.y*q.y;
}
inline ll cross(Vector p,Vector q){
return p.x*q.y-p.y*q.x;
}
inline ll sgn(ll x){
if(x==0) return 0;
else if(x>0) return 1;
else return -1;
}
bool is_cross(point A,point B,point C,point D){
if(max(A.x,B.x)>=min(C.x,D.x)&&max(C.x,D.x)>=min(A.x,B.x)&&max(A.y,B.y)>=min(C.y,D.y)&&max(C.y,D.y)>=min(A.y,B.y)){
if(sgn(cross(C-A,B-A))*sgn(cross(D-A,B-A))<=0&&sgn(cross(A-C,D-C))*sgn(cross(B-C,D-C))<=0) return 1;//不要直接乘,防止溢出
else return 0;
}else return 0;
}
int n;
point A[maxn+5],B[maxn+5];
map< pair<ll,ll>,ll>vis;
void get_cross(point A,point B,point C,point D){
ll S1=abs(cross(C-A,B-A));
ll S2=abs(cross(D-A,B-A));
Vector v=D-C;
if(v.x*S1%(S1+S2)!=0||v.y*S1%(S1+S2)!=0) return;
v=v*S1/(S1+S2);
point P=C+v;
vis[make_pair(P.x,P.y)]++;
}
ll get_ans(ll a){//x*(x-1)/2=a
ll x=(1+sqrt(1+8*a))/2;
return floor(x);
}
int main(){
ll ans=0;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld %lld %lld %lld",&A[i].x,&A[i].y,&B[i].x,&B[i].y);
Vector v=B[i]-A[i];
ans+=gcd(abs(v.x),abs(v.y))+1;
}
// printf("debug: %lld\n",ans);
for(int i=1;i<=n;i++){
for(int j=i+1;j<=n;j++){
if(is_cross(A[i],B[i],A[j],B[j])){
get_cross(A[i],B[i],A[j],B[j]);
}
}
}
for(map< pair<ll,ll>, ll>::iterator it=vis.begin();it!=vis.end();it++){
ll tim=it->second;
tim=get_ans(tim);
ans-=tim-1;
}
printf("%lld\n",ans);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号