二叉查找树及B-树、B+树、B*树变体

动态查找树主要有二叉查找树（Binary Search Tree），平衡二叉查找树（Balanced Binary Search Tree）， 红黑树 (Red-Black Tree )，

都是典型的二叉查找树结构，查找的时间复杂度 O(log2-N) 与树的深度相关，降低树的深度会提高查找效率，于是有了多路的B-tree/B+-tree/ B*-tree (B~Tree)。

二叉查找树

二叉查找树即搜索二叉树，或者二叉排序树（BSTree）。

一、关于二叉查找树

二叉查找树（Binary Search Tree）是指一棵空树或者具有下列性质的二叉树：
1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点，这个特征很重要，可以帮助理解二叉排序树的很多操作。
二叉查找树具有很高的灵活性，对其优化可以生成平衡二叉树，红黑树等高效的查找和插入数据结构。

二、基本性质

（1）二叉查找树是一个递归的数据结构，对二叉查找树进行中序遍历，可以得到一个递增的有序序列。
（2）二叉查找树上基本操作的执行时间和树的高度成正比。

对一棵n个节点的完全二叉树来说，树的高度为lgn，这些操作的最坏情况运行时间为O(lg n)，而如果是线性链表结构，这些操作的最坏运行时间是O(n)。
一棵随机构造的二叉查找树的期望高度为O(lg n)，但实际中并不能总是保证二叉查找树是随机构造的，
有些二叉查找树的变形能保证各种基本操作的最坏情况性能，比如红黑树的高度为O(lg n)，而B树对维护随机访问的二级存储器上的数据库特别有效。

注意对复杂度的理解，所谓的O(lg n)就是指复杂度是对数级别，是数量级的比较，和对数的底数其实没关系，

只要底数是大于1的，就是相同的数量级，有些书上说二叉查找树的复杂度是O(log2-n)，指的是相同的时间复杂度。

三、前驱和后继节点

一个节点的后继是该节点的后一个，即比该节点键值稍大的节点。
给定一个二叉查找树中的节点，找出在中序遍历顺序下某个节点的前驱和后继。
如果树中所有关键字都不相同，则某一节点x的前驱就是小于key[x]的所有关键字中最大的那个节点，后继即是大于key[x]中的所有关键字中最小的那个节点。根据二叉查找树的结构和性质，不用对关键字做任何比较，就可以找到某个节点的前驱和后继。

四、查找、插入与删除

（1）查找
利用二叉查找树左小右大的性质，可以很容易实现查找任意值和最大/小值。

在二叉查找树中查找一个给定的关键字k的过程与二分查找很类似，

首先是关键字k与树根的关键字进行比较，如果k比根的关键字大，则在根的右子树中查找，否则在根的左子树中查找，重复此过程，直到找到与遇到空节点为止。

在二叉查找树中查找x的过程如下：
1.若二叉树是空树，则查找失败。
2.若x等于根节点的数据，则查找成功，否则。
3.若x小于根节点的数据，则递归查找其左子树，否则。
4.递归查找其右子树。

（2）插入
二叉树查找树b插入操作x的过程如下：
1.若b是空树，则直接将插入的节点作为根节点插入。
2.x等于b的根节点的数据的值，则直接返回，否则。
3.若x小于b的根节点的数据的值，则将x要插入的节点的位置改变为b的左子树，否则。
4.将x要出入的节点的位置改变为b的右子树。

（3）删除

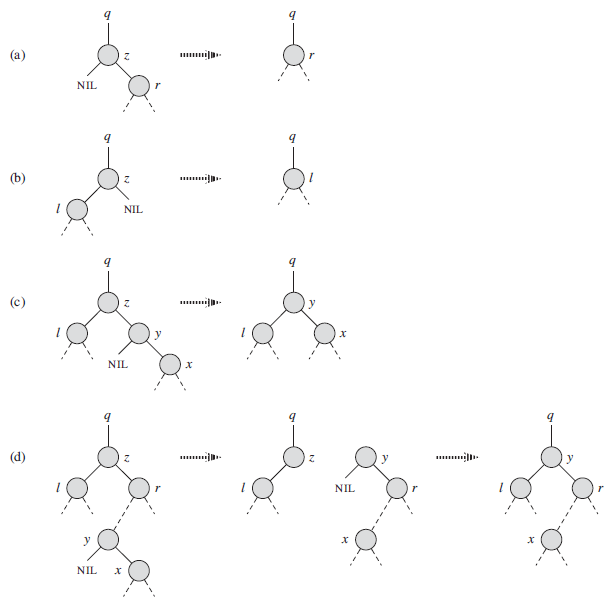
假设从二叉查找树中删除给定的结点z，分三种情况讨论：
1.节点z为叶子节点，没有孩子节点，那么直接删除z，修改父节点的指针即可。
2.节点z只有一个子节点或者子树，将节点z删除，根据二叉查找树的性质，将z的父节点与子节点关联就可以了。
3.节点Z有两个子节点，删除Z该怎样将Z的父结点与这两个孩子结点关联呢？
在删去节点Z之后，为保持其它元素之间的相对位置不变，可按中序遍历保持有序进行调整。
这种情况下可以用Z的后继节点来替代Z。
实现方法就是将后继从二叉树中删除，将后继的数据覆盖到Z中。

五、代码实现

public class BinarySearchTree <T extends Comparable<? super T>>{

	//节点数据结构 静态内部类
	static class BinaryNode<T>{
		T data;
		BinaryNode<T> left;
		BinaryNode<T> right;
		public BinaryNode(){
			data=null;
		}
		public BinaryNode(T data) {
			this(data,null,null);
		}
		public BinaryNode(T data,BinaryNode<T> left,BinaryNode<T> right){
			this.data=data;
			this.left=left;
			this.right=right;
		}
	}
	
	//私有的头结点
	private BinaryNode<T> root;
	
	//构造一棵空二叉树
	public BinarySearchTree(){
		root=null;
	}
	//二叉树判空
	public boolean isEmpty(){
		return root==null;
	}
	//清空二叉树
	public void clear(){
		root=null;
	}
	
	//检查某个元素是否存在
	public boolean contains(T t){
		return contains(t,root);
	}
	
	/**
	 * 从某个节点开始查找某个元素是否存在
	 * 在二叉查找树中查找x的过程如下：
	 * 1、若二叉树是空树，则查找失败。
	 * 2、若x等于根结点的数据，则查找成功，否则。
	 * 3、若x小于根结点的数据，则递归查找其左子树，否则。
	 * 4、递归查找其右子树。
	 */
	public boolean contains(T t,BinaryNode<T> node){
		if(node==null){
			return false;
		}
		/**
		 * 这就是为什么使用Comparable的泛型
		 * compareTo的对象也必须是实现了Comparable接口的泛型,
		 * 所以参数必须是BinaryNode<T> node格式
		 */
		int result=t.compareTo(node.data);
		if(result>0){//去右子树查找
			return contains(t,node.right);
		}else if(result<0){//去左子树查找
			return contains(t,node.left);
		}else{
			return false;			
		}
	}
	
	//插入元素
	public void insert(T t){
		root=insert(t,root);
	}
	
	/**
	 * 将节点插入到以某个节点为头的二叉树中
	 * 这个插入其实也是一个递归的过程
	 * 递归最深层的返回结果一个包含要插入的节点子树的头节点
	 */
	public BinaryNode insert(T t,BinaryNode<T> node){
		//如果是空树，直接构造一棵新的二叉树
		if(node==null){
			return new BinaryNode<T>(t);
		}
		
		int result=t.compareTo(node.data);
		
		if(result<0){
			node.left=insert(t,node.left);
		}else if(result>0){
			node.right=insert(t,node.right);
		}else{
			;//即要插入的元素和头节点值相等，直接返回即可
		}
		return node;
	}
	
	
	/**
	 * 删除元素
	 * 返回调整后的二叉树头结点
	 */
	public BinaryNode delete(T t){
		return delete(t,root);
		
	}
	
	/**
	 * 在以某个节点为头结点的树结构中删除元素
	 * 首先需要找到该关键字所在的节点p，然后具体的删除过程可以分为几种情况：
	 * p没有子女，直接删除p
	 * p有一个子女，直接删除p
	 * p有两个子女，删除p的后继q（q至多只有一个子女）
	 * 确定了要删除的节点q之后，就要修正q的父亲和子女的链接关系，
	 * 然后把q的值替换掉原先p的值，最后把q删除掉
	 */
	public BinaryNode delete(T t,BinaryNode<T> node){
		if(node==null){//节点为空还要啥自行车
			return node;
		}
		/**
		 * 首先要找到这个节点，所以还是得比较
		 */
		int result=t.compareTo(node.data);
		
		/**
		 * 去左半部分找这个节点，
		 * 找到节点result==0,这个递归就停止
		 */
		if(result<0){
			node.left=delete(t,node.left);
		}else if(result>0){//去右半部分找这个节点
			node.right=delete(t,node.right);
		}
		/**
		 * 如果这个节点的左右孩子都不为空，那么找到当前节点的后继节点，
		 * 
		 */
		if(node.left!=null && node.right!=null){
			/**
			 * node节点的右子树部分的最小节点，实际上就是它的后继节点
			 * 得到后继节点的值
			 */
			node.data = findMin(node.right).data;  
			/**
			 * 这个过程并不是删除后继节点，是一步一步的把所有的节点都替换上来
			 */
	        node.right = delete(node.data,node.right);  
		}else{
			/**
			 * 如果二叉搜索树中一个节点是完全节点，
			 * 那么它的前驱和后继节点一定在以它为头结点的子树中，应该是这样的
			 * 来到了只有一个头节点和一个子节点的情况
			 */
			node = (node.left!=null)?node.left:node.right; 
		}
		//此处的node，是经过调整后的传入的root节点
		return node;
		
	}
	
	/**
	 * 返回二叉树中的最小值节点
	 * 此时无比想念大根堆和小根堆
	 */
	public BinaryNode<T> findMin(BinaryNode node){
		if(node==null)
			return null;	
		/**
		 * 如果node不为空，就递归的去左边找
		 * 最小值节点肯定是左孩子为空的节点
		 */
		if(node.left!=null)
			node=findMin(node.left);
		return node;
	}
	
}

　　

B-树、B+树、B*树变体

关于这B树以及B树的两种变体，其实很好区分，

相比B树，B+树不维护关键字具体信息，不考虑value的存储，所有的我们需要的信息都在叶子节点上，

B*树在B+树的基础上增加了非叶子节点兄弟间的指针，在某些场景效率更高，

主要掌握B树的操作，也就掌握了这两种变体树的操作。

1.B树（B-tree），即B-树

B-树是为了磁盘或其它存储设备而设计的一种多叉平衡查找树。

（1）B-Tree的接点结构
B-tree中，每个结点包含：
本结点所含关键字的个数；
指向父结点的指针；
关键字；
指向子结点的指针数组；

#define Max l000 //结点中关键字的最大数目：Max=m-1，m是B-树的阶
#define Min 500 //非根结点中关键字的最小数目：Min=m/2-1
typedef int KeyType； //KeyType关键字类型由用户定义
typedef struct node{ //结点定义中省略了指向关键字代表的记录的指针
  　int keynum； //结点中当前拥有的关键字的个数，keynum<<Max
  　KeyType key[Max+1]； //关键字向量为key[1..keynum]，key[0]不用。
  　struct node *parent； //指向双亲结点
  　struct node *son[Max+1]；//指向孩子结点的指针数组，孩子指针向量为son[0..keynum]
 }BTreeNode；
typedef BTreeNode *BTree；

（2）B-tree的特点

• B-tree是一种多路搜索树（并不是二叉的），对于一棵M阶树：
• 定义任意非叶子结点最多只有M个孩子；且M>2；
• 根结点的孩子数为[2, M]，除非根结点为叶子节点；
• 除根结点以外的非叶子结点的儿子数为[M/2, M]；
• 非叶子结点的关键字个数=指向儿子的指针个数-1；
• 每个非叶子结点存放至少M/2-1（取上整）和至多M-1个关键字；
• 非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；
• 非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；
• 所有叶子结点位于同一层；

以M=3的一棵3阶B树为例：

一棵包含了24个英文字母的5阶B树的结构：

（3）B-tree高度与复杂度

B树的高度是，而不是其它几种树的H=log2n，其中T为度数（每个节点包含的元素个数），即所谓的阶数，n为总元素个数或总关键字数。

B树查找的时间复杂度为O(Log2-N)，下面是参考推导过程：

其中M为设定的非叶子结点最多子树个数，N为关键字总数；所以B-树的性能总是等价于二分查找（与M值无关），也就没有AVL树平衡的问题。

 

2.B-tree的基本操作

（1）查找操作

在B-树中查找给定关键字的方法类似于二叉排序树上的查找。不同的是在每个结点上确定向下查找的路径不一定是二路而是keynum+1路的。
对结点内的存放有序关键字序列的向量key[l..keynum] 用顺序查找或折半查找方法查找。若在某结点内找到待查的关键字K，则返回该结点的地址及K在key[1..keynum]中的位置；否则，确定K在某个key[i]和key[i+1]之间结点后，从磁盘中读son[i]所指的结点继续查找。直到在某结点中查找成功；或直至找到叶结点且叶结点中的查找仍不成功时，查找过程失败。

 

 BTreeNode *SearchBTree(BTree T，KeyType K，int *pos)
 { //在B-树T中查找关键字K，成功时返回找到的结点的地址及K在其中的位置*pos
//失败则返回NULL，且*pos无定义
  int i；
  T→key[0]=k; //设哨兵．下面用顺序查找key[1..keynum]
  for(i=T->keynum；K<t->key[i];i--)； //从后向前找第1个小于等于K的关键字
  if(i>0 && T->key[i]==1){ //查找成功，返回T及i
    *pos=i；
    return T；
   } //结点内查找失败，但T->key[i]<K<T->key[i+1]，下一个查找的结点应为
     //son[i]
  if(!T->son[i]) //*T为叶子，在叶子中仍未找到K，则整个查找过程失败
    return NULL；
    //查找插入关键字的位置，则应令*pos=i，并返回T，见后面的插入操作
  DiskRead(T->son[i])； //在磁盘上读人下一查找的树结点到内存中
  return SearchBTree(T->Son[i]，k，pos)； //递归地继续查找于树T->son[i]
 }

　　

（2）查找操作的时间开销
B-树上的查找有两个基本步骤：
1.在B-树中查找结点，该查找涉及读盘DiskRead操作，属外查找；
2.在结点内查找，该查找属内查找。
查找操作的时间为：
1.外查找的读盘次数不超过树高h，故其时间是O(h)；
2.内查找中，每个结点内的关键字数目keynum<m(m是B-树的阶数)，故其时间为O(nh)。
注意：
1.实际上外查找时间可能远远大于内查找时间。
2.B-树作为数据库文件时，打开文件之后就必须将根结点读人内存，而直至文件关闭之前，此根一直驻留在内存中，故查找时可以不计读入根结点的时间。

（3）插入操作

 插入一个元素时，首先在B树中是否存在，如果不存在，即在叶子结点处结束，然后在叶子结点中插入该新的元素，注意：如果叶子结点空间足够，这里需要向右移动该叶子结点中大于新插入关键字的元素，如果空间满了以致没有足够的空间去添加新的元素，则将该结点进行“分裂”，将一半数量的关键字元素分裂到新的其相邻右结点中，中间关键字元素上移到父结点中（当然，如果父结点空间满了，也同样需要“分裂”操作），而且当结点中关键元素向右移动了，相关的指针也需要向右移。如果在根结点插入新元素，空间满了，则进行分裂操作，这样原来的根结点中的中间关键字元素向上移动到新的根结点中，因此导致树的高度增加一层。

（4）删除操作

首先查找B树中需删除的元素,如果该元素在B树中存在，则将该元素在其结点中进行删除，如果删除该元素后，首先判断该元素是否有左右孩子结点，如果有，则上移孩子结点中的某相近元素到父节点中，然后是移动之后的情况；如果没有，直接删除后，移动之后的情况。

3.B+树（B+-tree）

B+-tree是应文件系统所需而产生的一种B-tree的变形树。

（1）B树和B+树的对比
一棵m阶的B+树和m阶的B树的异同点在于：
1.有n棵子树的结点中含有n-1 个关键字；
2.所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大的顺序链接。 (而B 树的叶子节点并没有包括全部需要查找的信息)
3.所有的非终端结点可以看成是索引部分，结点中仅含有其子树根结点中最大（或最小）关键字。 (而B 树的非终节点也包含需要查找的有效信息)
（2）为什么说B+-tree比B 树更适合实际应用中操作系统的文件索引和数据库索引？

•  B+-tree的磁盘读写代价更低

B+-tree的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B 树更小。

如果把所有同一内部结点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。

一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
举个例子，假设磁盘中的一个盘块容纳16bytes，而一个关键字2bytes，一个关键字具体信息指针2bytes。

一棵9阶B-tree(一个结点最多8个关键字)的内部结点需要2个盘快。而B+ 树内部结点只需要1个盘快。当需要把内部结点读入内存中的时候，B 树就比B+ 树多一次盘块查找时间(在磁盘中就是盘片旋转的时间)。

• B+-tree的查询效率更加稳定

由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

4.B*树（B*-tree）

B*-tree是B+-tree的变体，在B+树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，

B*树中非根和非叶子结点再增加指向兄弟的指针；

B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。

下图是一棵典型的B*树：