树上启发式合并学习笔记

谈到书上启发式合并不能忽略的两篇文章：
Tutorial: Sack (dsu on tree)
Explanation: dsu on trees (small to large)

引入

启发式算法大家最熟悉的一定是并查集的按秩合并了，合并的代码是这样的：

void merge(int x, int y)
{
   x = find(x), y = find(y);
   if (siz[x] < siz[y])
       swap(x, y);
   fa[y] = x, siz[x] += siz[y];
}

在这里，对于两个大小不一样的集合，我们将小的集合合并到大的集合中，以降低复杂度。

但是像这样简单以小并大的题实在是太少了，我们把操作扩展到树上，看看一般的具有这样优良性质的题可以如何做。

引例

给出一棵 \(n\) 个节点以 \(1\) 为根的树，节点 \(u\) 的颜色为 \(c_u\)，现在对于每个结点 \(u\) 询问 \(u\) 子树里颜色 \(c\) 一共出现了多少次。
\(n\le 2\times 10^5\)。

我们可以发现这个问题的几个特征：树上 没有修改 离线

能想到用什么方法来做？？

A： 离线是什么？我数据结构什么都不知道
恭喜！这类题大部分都可以用其他数据结构（线段树合并/树套树等）维护并AC，
但是对于离线的问题，有没有更简单而不用繁琐地去调代码的方法？

B：莫队、树上莫队！为什么不用？
不行，莫队带根号，我要 log
B：加回滚！

如果再简单一点呢？
既然支持离线，考虑预处理后 \(O(1)\) 输出答案。

做法

int cnt[N];
void add(int u, int p, int x)
{
    cnt[col[u]] += x;
    for(int v : g[u])
        if(v != p)
            add(v, u, x)
}
void dfs(int u, int p)
{
    add(u, p, 1);
    //now cnt[c] is the number of vertices in subtree of vertex u that has color c. You can answer the queries easily.
    add(u, p, -1);
    for(int v : g[u])
        if(v != p)
            dfs(v, u);
}

直接暴力 dfs 处理的时间复杂度为 \(O(n^2)\)，即对每一个子节点进行一次遍历。可以发现，每个节点的答案由其子树和其本身得到，然而这些信息都被我们浪费了。

我们可以先预处理出每个节点子树的大小和它的重儿子，再用 \(cnt_i\) 表示颜色 \(i\) 的出现次数，\(ans_u\) 表示结点 \(u\) 的答案。

遍历一个节点 \(u\)，我们按以下的步骤进行遍历：

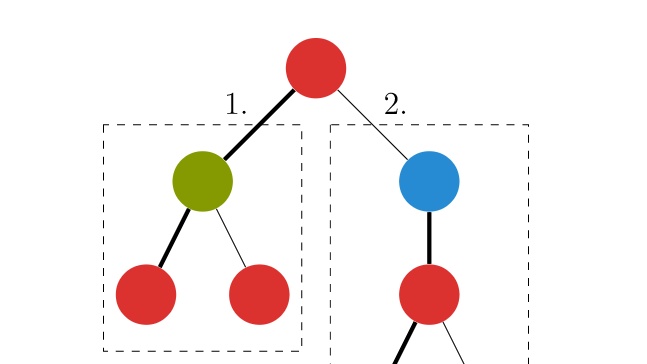
1. 先遍历 \(u\) 的轻儿子，并计算答案，但 不保留 遍历后它对 \(cnt\) 数组的影响；
2. 遍历它的重儿子，保留它对 \(cnt\) 数组的影响；
3. 再次遍历 \(u\) 的轻儿子的子树结点，加入这些结点的贡献，以得到 \(u\) 的答案。

实现

1. STL vector

// implemented by STL vector
vector<int> vec[N];
int cnt[N];
void dfs(int u, int p, bool keep)
{
    for (int v : g[u])
        if (v != p && v != son[u])
            dfs(v, u, 0);
    if (son[u])
        dfs(son[u], u, 1), vec[u] = vec[son[u]];
    vec[u].push_back(u), cnt[col[u]]++;
    for (int v : g[u])
        if (v != p && v != son[u])
            for (int x : vec[v])
                cnt[col[x]]++, vec[u].push_back(x);
    // now cnt[c] is the number of vertices in subtree of vertex u that has color c.
    if (!keep)
        for (int v : vec[u])
            cnt[col[v]]--;
}

很明显，在注释的位置，vec[u] 包含了子树的所有节点，我们对子树的暴力更新就是依靠里面存储的信息实现的。

2. 增量函数

int hev, cnt[N];
void add(int u, int p, int x)
{
    cnt[col[u]] += x;
    for(int v : g[u])
        if(v != p && v != hev)
            add(v, u, x);
}
void dfs(int u, int p, bool keep)
{
    for(int v : g[u])
        if(v != p && v != son[u])
            dfs(v, u, 0);  // run a dfs on small childs and clear them from cnt
    if(son[u] != -1)
        dfs(son[u], u, 1), hev = son[u];  // bigChild marked as big and not cleared from cnt
    add(u, p, 1);
    //now cnt[c] is the number of vertices in subtree of vertex u that has color c. You can answer the queries easily.
    hev = 0;
    if(!keep)
        add(u, p, -1);
}

这份代码是没有任何修改的模板，对于不同的题目，只需依情况改变 add 函数即维护答案的部分即可。

3. 性质：一个节点内子树的 dfn 序是连续的。
   在预处理时记录下每个节点的子树起始 dfn 和终止 dfn，更新使用 for 过去就行，只是一个常数优化。

习题

你已经学习 dsu 的经典使用方法，快来尝试一下这道模板题
CF246E Blood Cousins Return
CF570D Tree Requests
*SGU507 Treediff