电分笔记

电路分析基础

第一章 电路中的电压、电流

名词解析

• 支路：将每一个二端元件视为一条支路
• 节点：支路的连接点
• 回路：电路中的任意闭合路径
• 网孔：在回路内部不另含支路的回路
• 电导：电阻的倒数，单位为西门子
• VCR：元件特性
• // 表示对并联电阻求等效值
• 受控源:效果受其他电路控制(图标上会标)
  • VSVS:电压控制电压源
  • CCVS:电流控制电压源
  • VCCS:电压控制电流源
  • CCCS:电流控制电流源
  • 受控源为菱形，一般源为圆形

分压和分流

• 串联分压

\[u_k=\frac{R_k}{\sum_{k=1}^{n}R_k}u \]

• 并联分流

\[i_k=\frac{G_k}{\sum_{k=1}^{n}G_k}i,(G为电导) \]

第二章 网孔分析和节点分析

网孔分析

• KVL：对于任一集总电路中的任一回路，在任一时刻，沿着该回路的所有支路电压降的代数和为零
• 以网孔电流作为求解对象通过KVL方程求解��设多个网孔电流，对单一回路电压代数和为零
• 通过\(V=IR\)通过多个相接网孔的电流对当前网孔的影响可以并列多个方程,可求解得各网孔电流.
• 超网孔：两个以电流源或者受控电流源为公共边的网孔可当作同一个网孔处理

节点分析

• KCL：对于任一集总电路中的任一节点，在任意时刻，流入（流出）该节点的电流的代数和为零
• 通过对单个节点电压进行计算从而得出KCL，适用于有接地且节点比较少的系统
• 主要方式:设某个节点电压为0,通过\(I=US\)求解通过当前节点的总电流之和为零,得当前节点的电压

运算放大器

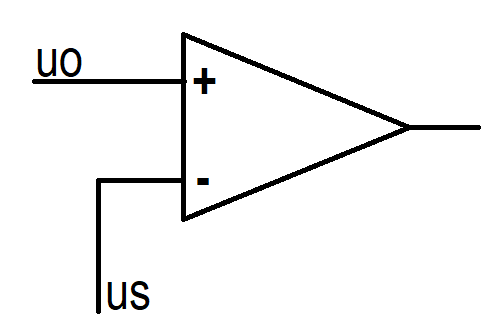
• 虚短：两个极电压相同\(u_s=u_0\)
• 虚断：无电流流过\(i=0\)

第三章 叠加和网络函数

• 电流源或电压源作为电路的输入起到激励的作用，其他元件作为响应

\[网络函数：H=\frac{响应}{激励} \]

• 若响应和激励在同一对端钮(单网孔)，则属策动点函数，如果不在同一对端钮(多网孔)，则属转移函数
• 叠加性：在有线性电阻，线性受控源，独立源构成的电路中，每一个元件的电流或电压可看成是每一个独立源单独作用于电路时，产生的电流和电压的叠加。
• 单独作用时，其余电压源作短路处理，其余电流源作开路处理。（受控源须保留，不能单独作用）
• 元件的功率不能用比例换算，需要重新计算电流和电压

第四章 分解方法及单\双口网络

分解方法

• 把给定网络划分为多个单口网络，规定划分处\(u\)和\(i\)的参考方向
• 分别求出单口网络的VCR
• 联立端口的电压电流
• 求和内部的电压电流

  明确的单口网络(可分解的)

  • 不包含控制变量在该网络以外的受控源
  • 单口网络的VCR与外接电路无关,常用外施电流求电压法和外施电压求电流法

置换定理

• 两个单口网络连接,已知端口电压和电流值,可以相同的电压源或电流源置换其中任意一个单口网络,置换定理适用于线性和非线性网络
• 置换时一种基于工作点相同的"等效"替换

等效定理

• 如果一个单口网络和另一个单口网络的电压,电流关系完全相同,即伏安特性曲线完全相同,则这两个单口网络等效
• 置换是特殊的等效

常见的等效规律和方法

• 电阻串联等于各电阻值和\(R'=R_1+R_2+...\)
• 电导并联等于各电导值和\(S'=S_1+S_2+...\)
• 串联电压源串联等于各电压值和\(U'=U_1+U_2+...\)
• 多电压源并联,值相同则等同于单个电压源的值,若不同则违背KVL方程,无解
• 网络与电压源并联,网络视为开路
• 多电流源并联等于各电流值和\(I'=I_1+I_2+...\)
• 多电流源串联,值相同则等同于单个电流源的值,若不同则违背KCL方程,无解
• 网络与电流源串联,网络视为短路
• 电压源串连电阻等同于电流源并联电阻,

\[R_s=R^\prime _s ~~~~~~u_s=i_sR^\prime _s ~~~~~~i_s=\frac{u_S}{R} \]

单口网络的等效电路

• 无独立源单口网络的等效电路:\(U=kI\)
  • 纯电阻电路等效于电阻
  • 含受控源的无源单口网络的等效电路等效于电阻,R可正可负
• 含独立源单口网络的等效电路:\(U=kI+b\)
  • 不含受控源等效于一个电压源串联一个正值电阻(靠计算得出,)
  • 含受控源等效于一电压源串联一电阻,电阻可正可负

戴维南定则

• 已知单口网络可等效成一个电压源串联一个电阻
• 做法:
  • 先将外接端口开路,计算端口电压\(U_{OC}\)
  • 计算等效电阻（两种方法）：
    • 1.外施电压(电流):用等效电路计算\(R_0\)(电压短路，电流断路���受控保留)
    • 2.将外接端口短路,计算端口的电流\(i_{SC}\)(电压电流方向不关联)
      • 计算戴维南等效电阻:
  \[R_o=\frac{U_{0C}}{i_{SC}} \]

诺顿定理(略显多余)

• 已知单口网络可等效成一个电流源串联一个电阻
• 做法:
  • 先求短路电流\(i_{SC}\)
  • 再将内部电压源用短路替代,求外部等效电阻\(R_0\)

直流电路最大功率传递定理

• 内外等效电阻相同时功率最大

电容和电感

• 电容和电感的电流参考关联方向都相当于电阻，流入为正，流出为负

  电容	电感
  \(q(t)=Cu_C(t)\)	\(y(t)=Li_L(t)\)
  \(i_C(t)=C\cfrac{dU_c}{dt}\)	\(U_L(t)=L\cfrac{di_L}{dt}\)
  \(U_c(t)=U_C(t_0)+\cfrac{1}{C}\int ^{t}_{t_0}i_c(\xi)d\xi\)	\(i_L(t)=i_L(t_0)+\cfrac{1}{L}\int ^{t}_{t_0}U_l(\xi)d\xi\)
  \(p(T)=u_c(t)i_c(t)\)	\(p(t)=U_L(t)i_L(t)\)
  \(w(t)=\cfrac{1}{2}Cu^2_c(t)\)	\(w(t)=\cfrac{1}{2}Li^2_L(t)\)
  电压不能跃变	电流不能跃变

第六章 一阶电路(即带电阻)

零状态响应

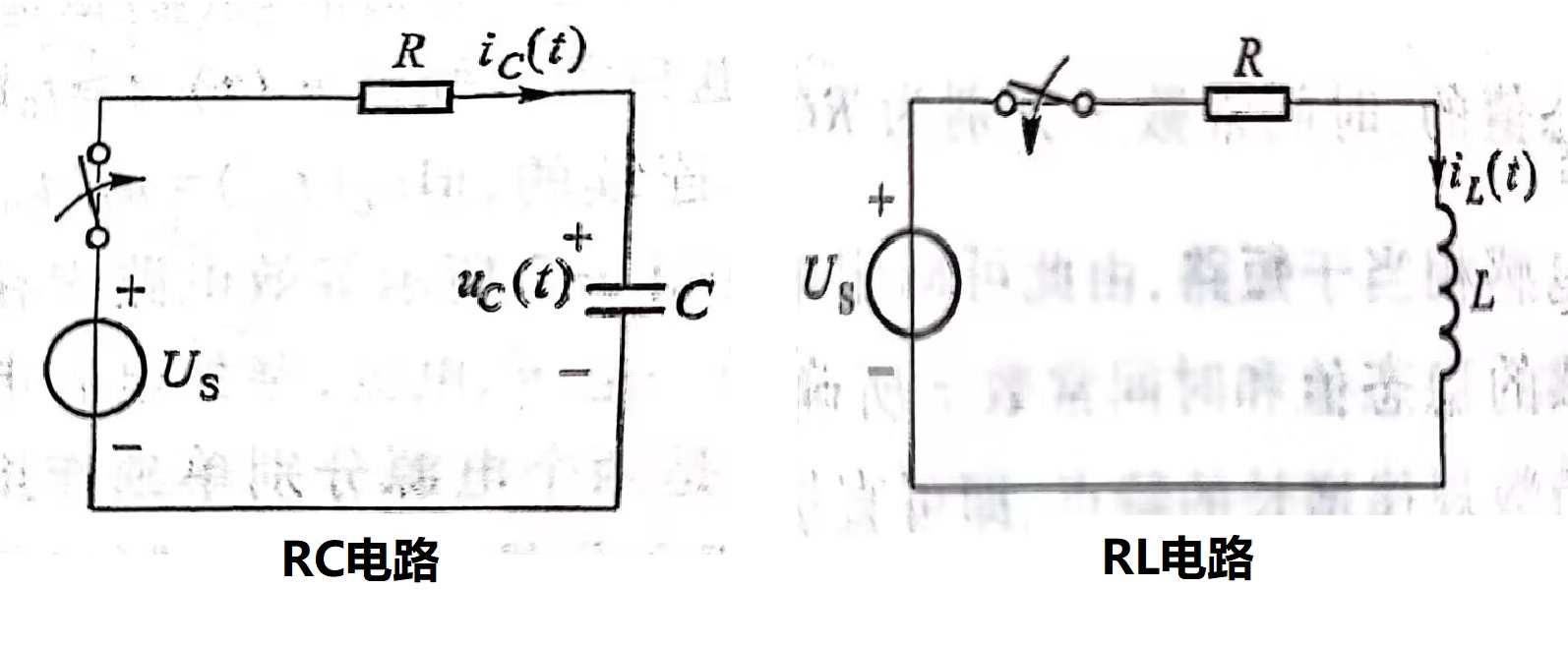
• 元件初始状态为0，施加外部源引起的响应
• 以电容为例，求解一阶微分方程

\[\left\{ \begin{aligned} Ri_c(t)+u_c(t)=RC\frac{du_c}{dt}+u_c=U_S \\ u_c(0)=0 \end{aligned} \right.\]

电容	电感
电压变化	电流变化
\(u_c(t)=U_s(1-e^{-\frac{1}{RC}t})\)	\(u_c(t)=\frac{U_s}{R}(1-e^{-\frac{R}{L}t})\)
电流通过电压计算	电压通过电流计算

冲激响应

• 零状态响应的广义
• 通过设定冲激函数\(\varepsilon(t-x)\):当时间大于x时施加冲激
• 对脉冲电压/电流进行叠加计算

零输入响应

• 仅依靠元件自身能量进行的响应(电流方向同零状态)
• 求解过程和零状态一样，\(U_s=0,u_c(0)=U_0\)

  电容	电感
  电压不突变	电流不突变
  \(u_c(t)=-U_0e^{-\frac{1}{RC}t}\)	\(u_c(t)=-i_0e^{-\frac{R}{L}t}\)
  电流通过电压计算	电压通过电流计算

全响应(终极大法)

• 叠加计算：全响应=零状态响应+零输入响应
• 时间常数\(\tau=RC~~or~~\cfrac{L}{R}\)
• 固有频率：\(-\cfrac{1}{\tau}\)
• 三要素：一阶，直流，R>0
  \[y(t)=y(\infty)+[y(0_+)-y(\infty)]e^{-\frac{t}{\Gamma}} \]

二阶电路

LC电路中的正弦震荡

• 可得联立的一阶微分方程

\[\left\{ \begin{aligned} C\frac{du_c}{dt}=-i_L \\ L\frac{di_L}{dt}=u_c \\ u_c(0)=0 \\ i_L(0)=0 \end{aligned} \right.\]

• 求解得(有问题)
  \[\left\{ \begin{aligned} u_c(t)=U_0cos(\omega_0t) \\ i_L(t)=C\omega_0U_0sin(\omega_0t) \end{aligned} \right.\]

• 没有电阻的情况下按正弦方式震荡

RLC串联电路零输入响应

• 零输入\(u_{oc}(t)=0\)，零状态的图先放零输入这了

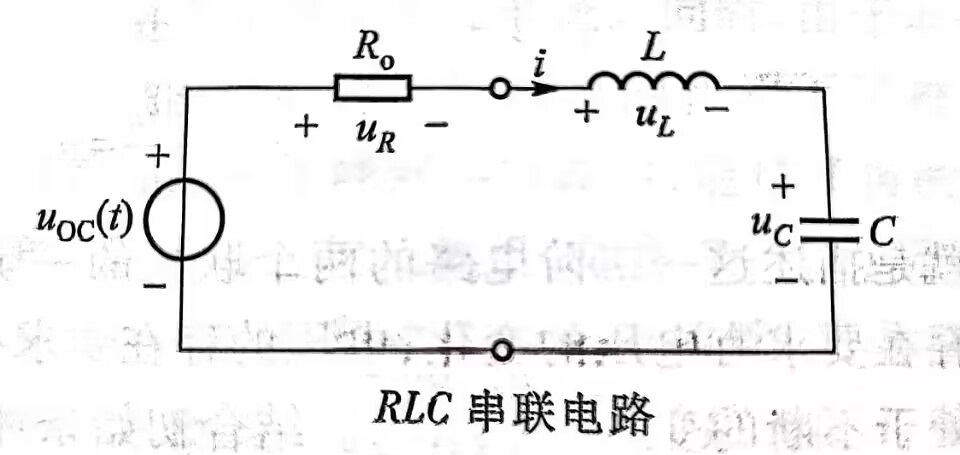
\[\left\{ \begin{aligned} i=C\frac{du_c}{dt} \\ u_L=L\frac{di}{dt}=LC\frac{d^2u_c}{dt^2}\\ u_R=Ri=RC\frac{du_c}{dt} \\ u(0)=0 \\ i(0)=0 \end{aligned} \right. \]

• 通过电压KVL联立微分方程,解得特征根

\[s_{1,2}=-\frac{R}{2L}\pm \sqrt{(\frac{R}{2L})^2-\frac{1}{LC}} \]

• 得阻尼电阻
  \[R_d=2\sqrt{\frac{L}{C}} \]

• 串联电阻与阻尼电阻的关系可分为过阻尼,临界,欠阻尼,分别各有一种方程求解
  • 过阻尼状态(俩特征根)：

\[u_C(t)=K_1e^{s_1t}+K_2e^{s_2t} \]

• 临界阻尼状态(一特征根)：

\[i_L(t)=(K_1+K_2t)e^{st} \]

• 欠阻尼(俩复数特征根)：

\[u_C(t)=e^{-at}[K_1cos(\omega_dt)+K_2sin(\omega_dt)] \]

RLC串联电路零状态响应

• TO DO:

GLC并联电路

• 由KCL方程求特征根：

\[s_{1,2}=-\frac{G}{2C}\pm \sqrt{(\frac{G}{2C})^2-\frac{1}{LC}} \]

• 得阻尼电导：

\[G_d=2\sqrt{\frac{C}{L}} \]

• 其余和串联一样

第八章 交流动态电路 相量法

复数

• 相量的复数表示（数学用\(i\),这里用\(j\)，因为电流抢了位置）

\[A=a_1+ja_2 \\ Re(a_1+ja_2)=a_1\small~~ 取实部 \large \\ Im(a_1+ja_2)=a_2\small~~ 取虚部 \]

• 相量角表示：（相量角不能直接相加，乘除方便）

\[A=a\angle \theta_a,B=b\angle \theta_b \\ A\cdot B=ab\angle (\theta_a+\theta_b) \\ \frac{A}{B}=\frac{a}{b}\angle (\theta_a-\theta_b)\]

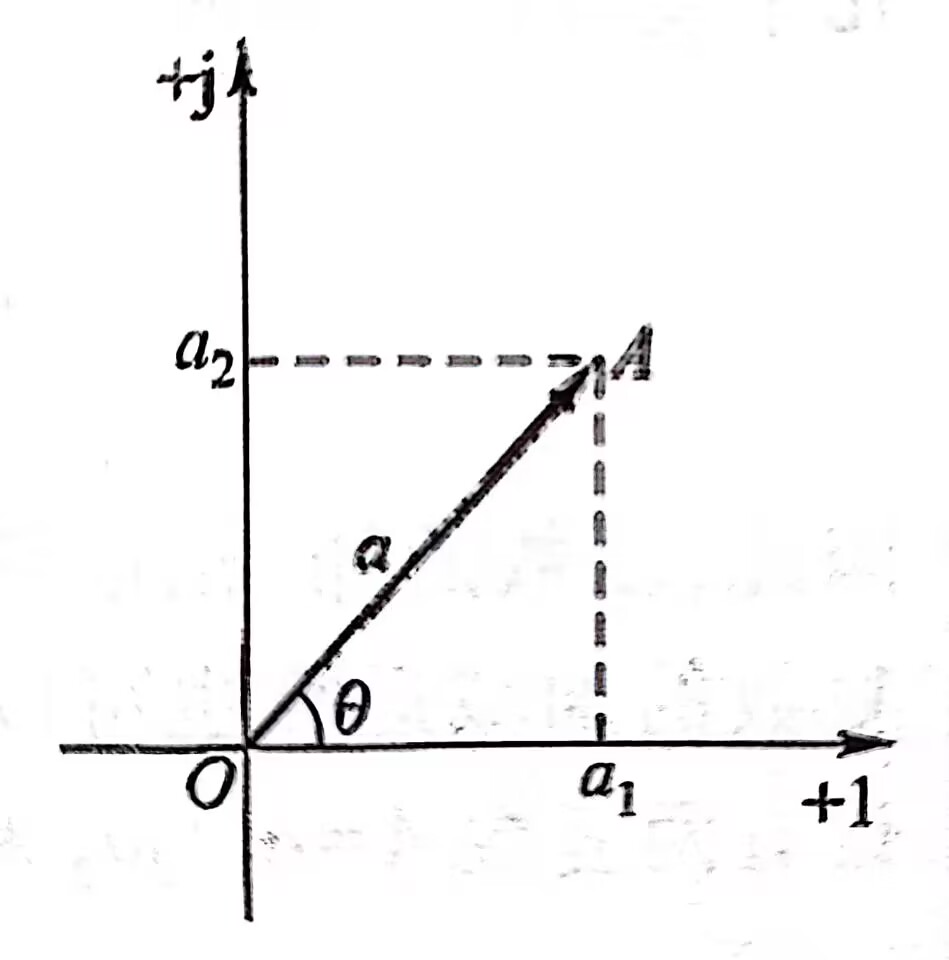
• 变化原理：欧拉恒等式

\[e^{j\theta}=cos\theta +jsin\theta \]

振幅相量

• 设正弦电压为：

\[u(t)=U_mcos(\omega t+\psi) \]

• 则电压向量为：

\[U^\prime=U_m\angle \psi \]

阻抗和导纳

• 定义元件在正弦��态时电压相量与电流相量之比定义为该文件的阻抗
• 电阻，电容，电感的阻抗(根据电压电流关系需要加正负号)

\[Z_R=R \\~\\ Z_C=-j\frac{1}{\omega C} ~~~\small电压滞后电流，先有电流再改变电压\large\\ ~\\ Z_L=j\omega L~~~\small电压超前电流，先改变电压再改变电流\]

• 阻抗的倒数定义为导纳
• 容抗，电容的阻抗。容纳，电容的导纳。其余同理。

相量模型

• 计算器的重要性
• 把所有元件都转换成复数形式，按一维电路计算，再将计算后的结果转化成向量(复数除法不好做可以直接变成向量角用加减法做),由向量再得出函数(向量角与函数之间不能用等号)
• 主要有网孔分析,节点分析,等效
• 两种等效模型:
  • \(Y(j\omega)\)也就是把电路的总电导求出来
  • \(Z(j\omega)\)总电阻

有效值向量

• 电流表,电压表读出的都是有效值,可理解为\(A=a\angle \theta_a\)中的\(a\)即为电表读数,但电表读数在解题时可以直接用,当作没有j方向的向量

正弦稳态功率和能量

电阻的平均功率

• 平均功率又称有功功率
• 对正弦电路求功率须用有效值求：\(\frac{1}{\sqrt 2}\)

电容电感的平均储能

• 电容电感都是储能元件，不消耗功率
• 将瞬时功率\(UI\)的振幅定义为电容电感的无功功率

\[Q_;=\omega LI^2=2\omega W_L \]

\[Q_C=-\omega CU^2=-2\omega W_C \]

• 可得电容无功功率为负，电感无功功率为正，且都为储能平均值的\(2\omega\)倍
• 无功功率单位为乏(\(var\))（很重要）

单口网络的功率

• 一般情况下，若单口网络端口电压和端口电流的相位差角为\(\varphi\)，则计算平均功率的公式为

\[P=UIcos\varphi=I^2Re[Z] \]

• 电工技术中把\(UI(\frac{1}{2}U_mI_m)\)称为视在功率，记作\(S\)，单位\(V\cdot A\)

\[S=UI \]

• 平均功率一般是小于视在功率的，要打个折扣，这个折扣就是\(cos\varphi\),记作\(\lambda\)，称为功率因素

\[\lambda=\frac{P}{S}=cos\varphi \]

• 若阻抗呈电感性，\(\varphi>0\)，电流滞后电压；阻抗呈电容性，\(\varphi<0\)，电流超前电压
• 则无功功率为

\[Q=UIsin\varphi=I^2Re[Z] \]

• 视在功率\(S\),平均功率\(P\)，无功功率\(Q\)的关系

\[S=\sqrt{P^2+Q^2} \]

复功率

• 设\(\dot U=U\angle \varPhi_u,\dot I=I\angle \varPhi_i\)

\[\dot U\dot I=UI\angle \varPhi_u+\varPhi_i=UI[cos(\varPhi_u+\varPhi_i)+jsin(\varPhi_u+\varPhi_i)] \]

• 要使直接获得实部为有功功率，虚部为无功功率，引入\(\dot I\)的共轭负量\(\dot I^*\)

\[\dot I^*=I\angle -\varPhi_i \\ \dot U\dot I^*=UI[cos(\varPhi_u-\varPhi_i)+jsin(\varPhi_u-\varPhi_i)]=P+jQ\]

• 将复量\(\dot U\dot I^*\)称为复功率或功率相量,记作\(\tilde{S}\)

\[\tilde{S}=\dot U\dot I^*=P+jQ=P+j2\omega(W_L-W_C) \]

• 复功率\(\tilde{S}\)的模即为视在功率

正弦稳态最大功率

• 设电源\(\dot U\)的内阻抗为\(Z_s=R_s+jX_s\)
• 第一种情况，负载的电阻和电抗均可独立的变化,负载的阻抗和内阻抗共轭：

\[Z_L=Z_s^*\small ~~~~~注意是共轭形式 \\ P_{max}=\frac{U_s^2}{4R_s}\]

• 第二种情况，负载阻抗角固定而模可改变，负载的模和内阻抗的模相等:

\[\lvert Z\lvert =\sqrt{R_s^2+X_s^2} \]

第十章 频率响应 多频正弦稳态电路

正弦稳态网络函数

• 对于相量模型，在单一激励的情况下，网络函数定义为

\[\frac{响应相量}{激励相量}=H(j\omega) \]

• 瞬时功率无法叠加，但是多个不同频率的输入源产生的功率可以直接叠加

RC低通电路

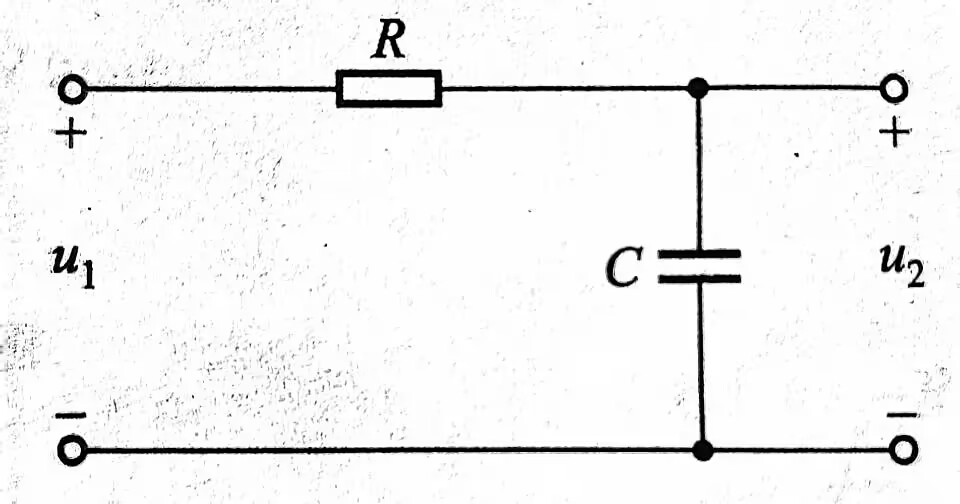
• 输出端与电容并联，低频信号可通过，高频信号不可通过，又称滞后网络。

\[ H_u=\frac{\dot U_2}{\dot U_1} \\~\\ \lvert H_u\lvert=\frac{U_2}{U_1}=\frac{1}{\sqrt{1+\omega^2R^2C^2}}\]

• 当\(\omega =\cfrac{1}{\tau}=\cfrac{1}{\sqrt{RC}}\)时，\(\lvert H_u\lvert=\cfrac{1}{\sqrt{2}}\)时，功率降低为\(\cfrac{1}{2}\)，因此\(\omega =\cfrac{1}{\tau}\)称为半功率点频率，记作\(\omega_c\)
• 工程技术上，把频率从0到\(\omega_c\)的范围定为这一低通滤波器的通频带，\(\omega_c\)记作截止频率

\[H_u=\cfrac{1}{1+j\cfrac{\omega}{\omega_c}} \]

RLC电路的谐振

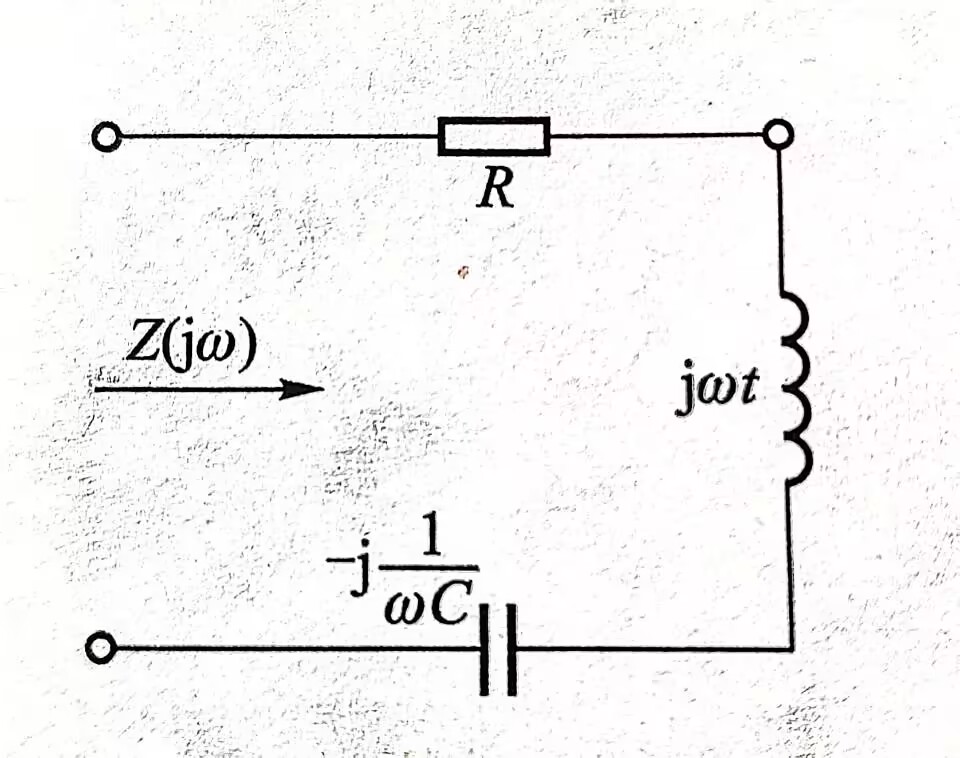
• 谐振现象：在某一频率的正弦激励下，同时含有电容，电感的电路中，整个电路表现为一个电阻

串联谐振

• 谐振频率记作\(\omega_0\)

\[\omega_0=\frac{1}{\sqrt{LC}} \]

• 当输入频率为谐振频率时，电容电感上电压相互抵消，但局部电压远大于外施电压，为外部电压的\(Q\)倍。\(Q\)称为\(RLC\)电路的品质因素

\[Q=\frac{\omega_0L}{R} \]

• 易得电阻越小，品质因数\(Q\)越高，可以更好的选择某一频率，排除其他频率成分，\(RLC\)电路的选择性越好
  
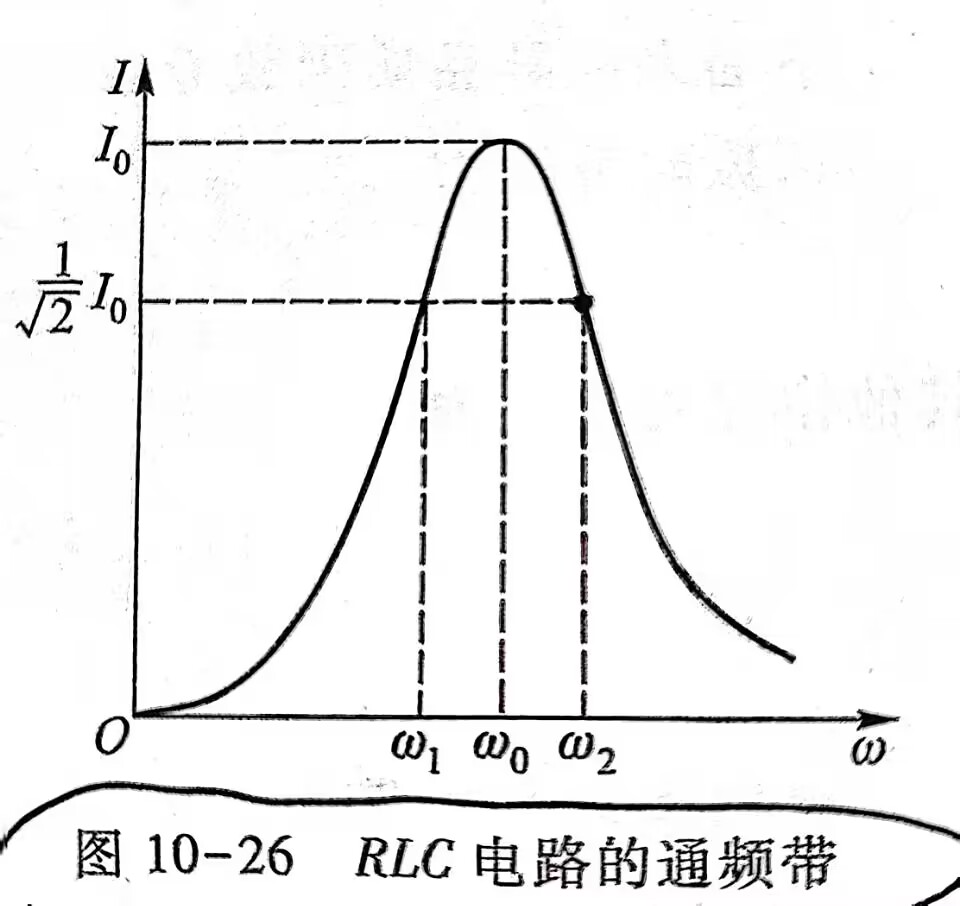
• 同样规定\(RLC\)电路的通频带为电流大于\(\cfrac{1}{\sqrt{2}}I_0\)时的频道，设半功率点\(\omega_1,\omega_2\)，则通频带

\[ \omega_1=-\frac{R}{2L}+\sqrt{(\frac{R}{2L})^2+\frac{1}{LC}}\\~\\ \omega_2=\frac{R}{2L}+\sqrt{(\frac{R}{2L})^2+\frac{1}{LC}}\\~\\ BW=\omega_2-\omega_1 \\~\\ \omega_0=\sqrt{\omega_1\omega_2}\]

并联谐振

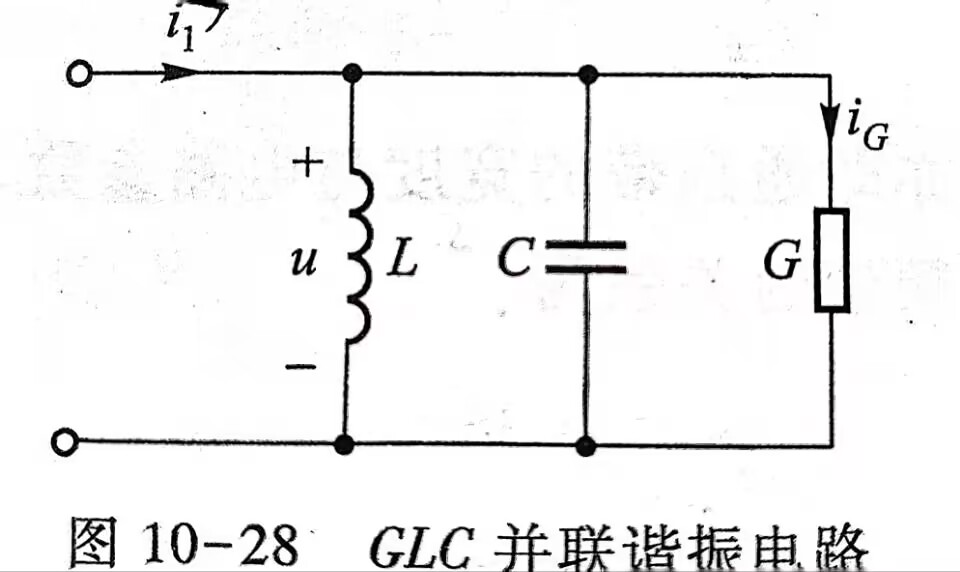
\[\omega_0=\frac{1}{\sqrt{LC}} \\~\\ Q==\frac{\omega_0C}{G}=\frac{1}{\omega_0LG}\\~\\ BW=\omega_2-\omega_1=\frac{\omega_0}{Q}\]

第十一章 耦合电感和理想变压器

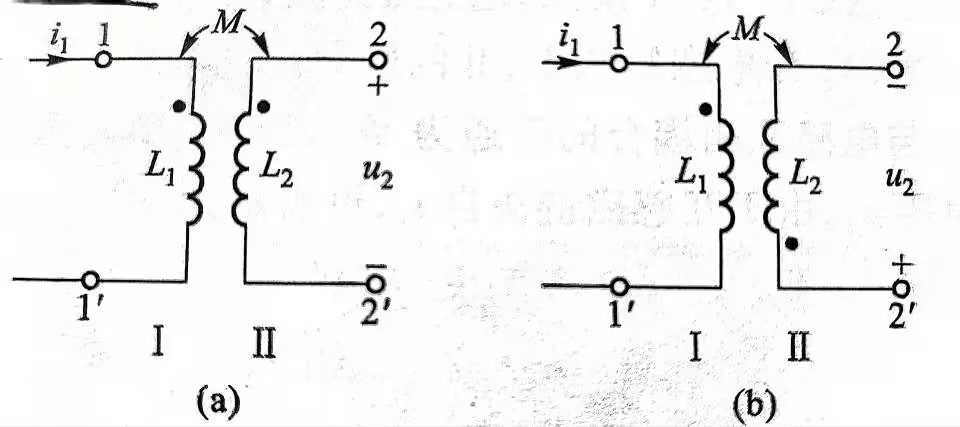
• 同名端：用‘\(\cdot\)’标出，产生电流参考方向的流出端（课本写的是流入端）
• 电流从一边的同名端流入，从另一半的同名端流出
• 感应电压值:\(M\cfrac{di}{dt}\)，感应电流值:\(j\omega M\dot I\)，\(M\)为互感系数

耦合电感的VCR

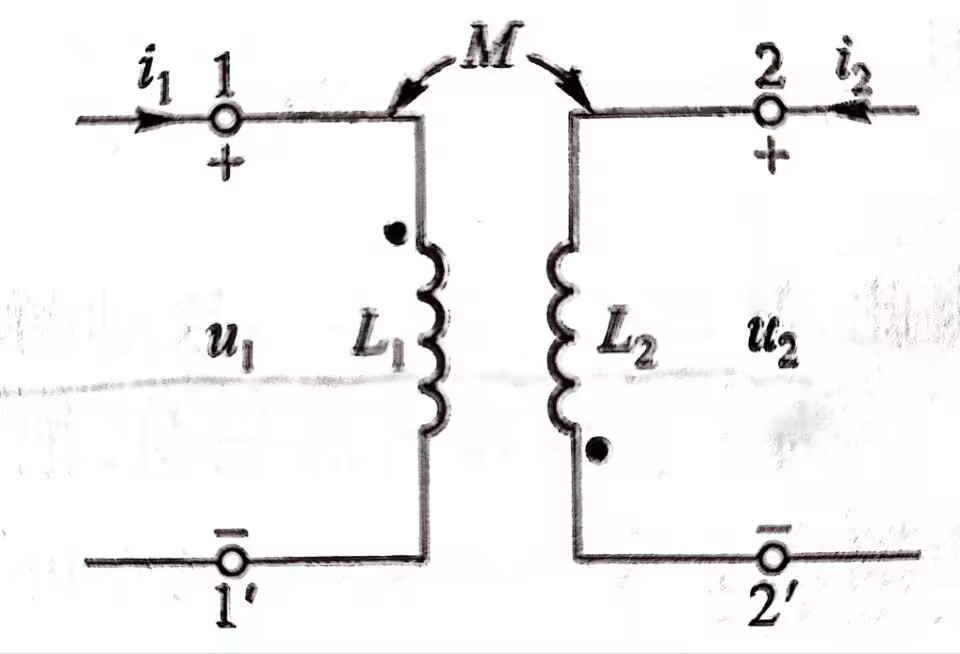
• 一般情况：

\[u_1=L_1\frac{di_1}{dt}-M\frac{di_2}{dt} \]

• 正弦稳态：

\[\dot U_1=j\omega L_1\dot I_1-j\omega M\dot I_2 \\~\\ \dot U_2=j\omega L_2\dot I_2-j\omega M\dot I_1\]

• 耦合系数:
• 全耦合：每一个线圈产生的磁通全部与另一个线圈相交链

\[M_{max}=\sqrt{L_1L_2} \]

• 耦合系数：

\[k=\frac{M}{M_{max}} \]

耦合等效

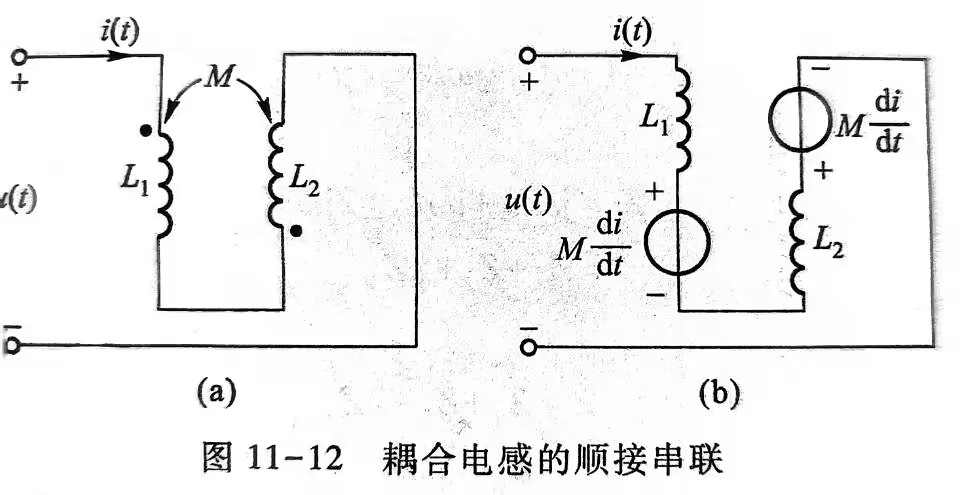
• 顺接串联耦合电感（异名相接）:

\[u(t)=L_1\frac{di}{dt}+M\frac{di}{dt}+L_2\frac{di}{dt}+M\frac{di}{dt} \]

\[L=L_1+L_2+2M \]

• 反接:

\[L=L_1+L_2-2M \]

• 同名相接并联耦合:

\[L=\frac{L_1L_2-M^2}{L_1+L_2-2M} \]

• 异名相接并联耦合

\[L=\frac{L_1L_2-M^2}{L_1+L_2+2M} \]

空心变压器分析 反映阻抗

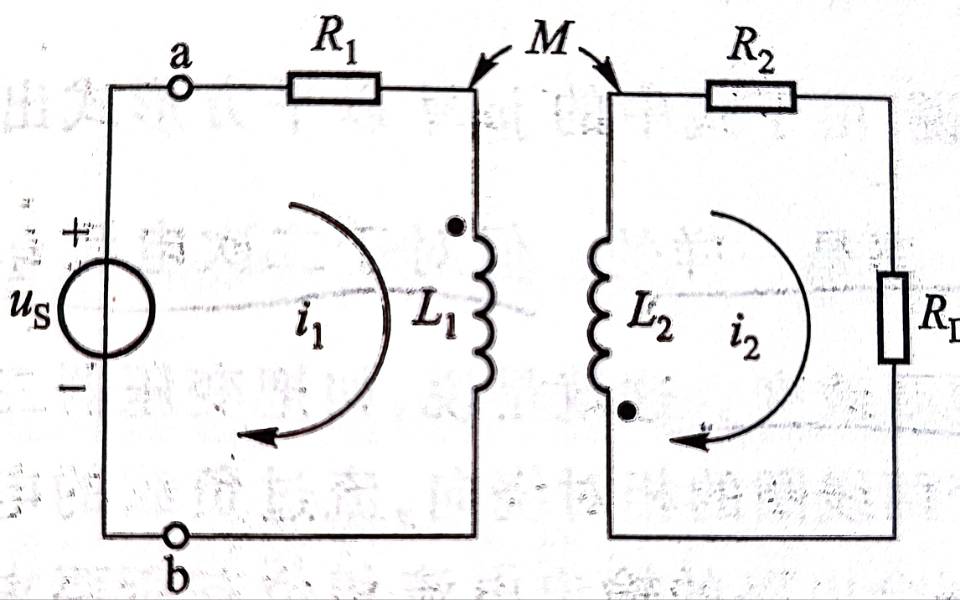
• 异名向上的反映阻抗,若是同名端向上，\(\dot I_1\)不变，\(\dot I_2\)变号，可以正常用电压电流做，不需要硬记公式
• 左侧输入端（网孔电流联立求解）：

\[\dot I_1=\cfrac{\dot U_S}{Z_{11}+\cfrac{\omega^2M^2}{Z_{22}}} \]

• 右侧输出端（电压除电阻）：

\[\dot I_2=\frac{-j\omega M\dot I_1}{Z_{22}} \]

耦合电感的去耦等效电路

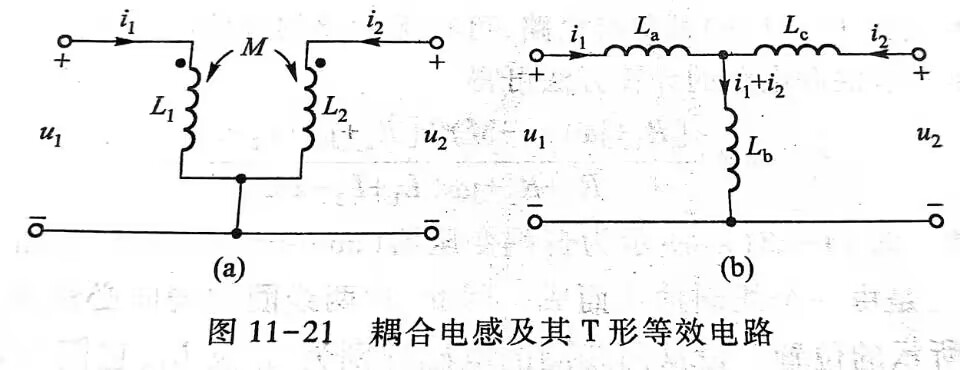
• 同名相接（如图）

\[\left.\begin{matrix}L_{a}=L_{1}-M\\ L_{b}=M\\ L_{c}=L_{2}-M\end{matrix}\right\} \]

• 若是异名相接，则

\[\left.\begin{matrix}L_{a}=L_{1}+M\\ L_{b}=-M\\ L_{c}=L_{2}+M\end{matrix}\right\} \]

理想变压器VCR

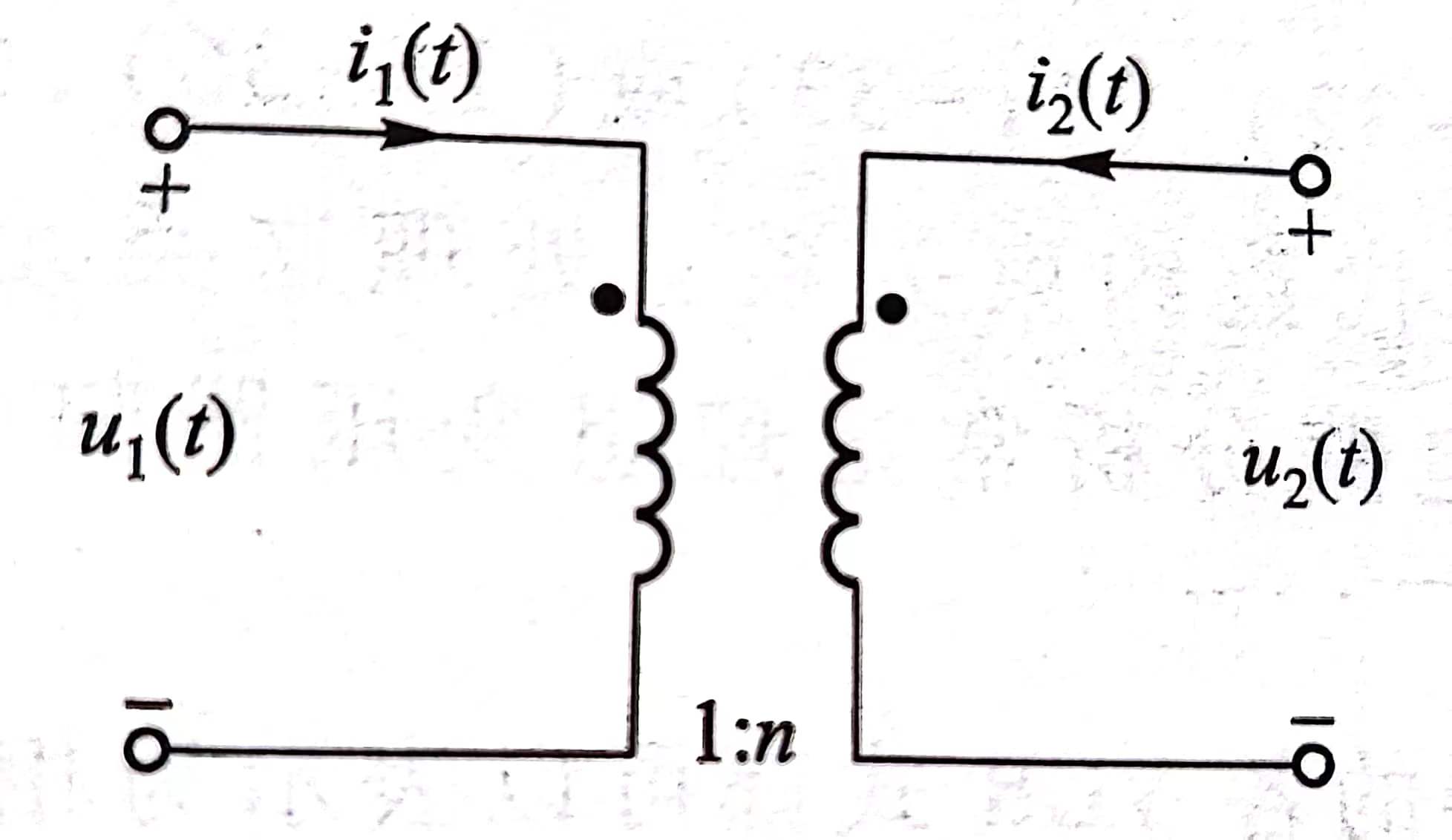
• 同名向上(功率相同),异名反向

\[u_2(t)=nu_1(t)~~,~~i_2(t)=-\frac{1}{n}i_1(t) \]

• 电压比由磁通量比（线圈比）决定

\[n=\frac{N_1}{N_2} \]

• 电阻转换（右侧往左侧）

\[Z_i(j\omega)=\frac{1}{n^2}Z_L(j\omega) \]