大物笔记

大学物理

质点力学

圆周运动

\[角速度: \omega=\frac{d\theta}{dt} \]

\[v=R\omega \]

\[向心加速度 a_n=v\omega =\frac{v^2}{R}=R\omega ^2 \]

牛顿运动定理

\[加速度：F=ma=\frac{dp}{dt} \]

\[重力：F=G\frac{m_1m_2}{r^2} \]

\[弹力：F=-kx \]

\[摩擦力：F_{fs,m}=\mu_sF_N \]

\[流体阻力：F=bv^2 \]

\[冲量: I=F\Delta t=\int ^{t_2}_{t_1} F(t) dt \]

\[质心的位置矢量：\vec {r_c}=\frac{m_1\vec{r_1}+m_2{r_2}+...+m_N\vec{r_N}}{m_1+m_2+...+m_N}= \frac{ \sum_{i=1}^{N}m_i\vec{r_i}}{m} \]

角动量

\[设质点t时刻位置矢量为\vec r，动量\vec p,受力\vec F，夹角为\varphi \]

\[定义角动量\vec L=\vec r \times \vec p \]

\[定义力矩\vec M =\vec r \times \vec F \]

\[角动量定理：\vec M=\frac{d\vec L}{dt} \]

\[冲量矩：\int ^{t_2}_{t_1} \vec Mdt=\vec {L_2}- \vec {L_1} \]

\[\small质点角动量的增量等于在该时间间隔内质点所受合力的冲量矩 \]

• 角动量守恒定律:如果质点系受到的对某一定点的合外力矩为零,则该质点系对这一定点的角动量守恒.

功和能

\[W=F\cdot \Delta r \]

\[P=\frac{dW}{dt} \]

保守力

• 若一对力的功和相对路径的形状无关,只取决于始末位置,则这一对力被称为保守力
• 设初位置为A,末位置为B,定义保守内力的功等于系统相应势能增量的负值:

\[W_{AB}=E_{pA}-E_{pB}=-\Delta E_p \]

• 万有引力势能:定义两个质点相距无穷远处时,系统的万有引力势能为零:

\[E_p=-\frac{Gm_1m_2}{r} \]

• 弹性势能:规定弹簧为自然长度时,弹性势能为零

\[E_p=\frac{1}{2}kx^2 \]

机械能守恒定律

• 若质点系在运动中只有保守内力做功,则系统的机械能守恒.

刚体力学

转动惯量

• 设刚体上第\(i\)个质点的质量为\(\Delta m_i\),距转动轴的距离为\(r_i\),定义刚体对z轴的转动惯量\(J\)
  \[J=\sum_{i=1}^{N}\Delta mr_i^2 \]

• 常用公式:
  \[J=\int ^{}_{V}r^2xdV~~(x=\rho,\sigma,\lambda) \]
  \[细杆绕一端旋转:\frac{1}{3}mL^2 \\ ~ \\ 细杆绕中点旋转:\frac{1}{12}mL^2 \\ ~\\圆环绕中心轴:mR^2\\ ~\\圆环绕直径:\frac{1}{2}mR^2\\ ~\\圆盘绕中心轴:\frac{1}{2}mR^2\\ ~\\圆盘绕直径:\frac{1}{4}mR^2\\ ~\\薄球壳绕轴:\frac{2}{3}mR^2\\ ~\\球体绕直径:\frac{2}{5}mR^2 \]

• 平行轴定理
  • 若刚体相对于通过其质心的转轴转动惯量为\(J_c\),则刚体相对于其他与质心轴距离为\(d\)的轴转动时转动惯量为:
  \[J=J_c+md^2 \]

• 垂直轴定理
  • 对于薄板型的刚体,与之垂直轴的转动惯量等于它对板面内的另外两个彼此垂直轴的转动惯量的合
  \[J_z=J_x+J_y \]

刚体定轴转动的功和能

• 力矩的功

\[dW=Md\theta \]

• 转动动能

\[E_k=\frac{1}{2}Jw^2 \]

气体动理论

热力学系统

• 孤立系统，无任何交换；封闭系统，能量交换；开放系统，物质能量都交换
• 温标:

\[T/K=t/^oC+273.15(一般取273) \]

• 摩尔气体常量

\[R=8.31J/(mol\cdot K) \]

\[pV=vRT=\frac{m}{M}RT \]

p为压强，V为体积，v为物质的量，m为气体质量，M为摩尔质量

• 玻耳兹曼常量

\[k=\frac{R}{N_A}=1.38\times10^{-23}J/K \]

\[p=nkT \]

压力和温度的微观解释

• \(n=N/V\)为分子数密度，即单位体积内的分子数
• 设分子的平均速度为\(\overline v\)
  \[\overline {v^2_x}=\overline {v^2_y}=\overline {v^2_z}=\frac{1}{3}\overline {v^2} \]

• 平均平动动能:
  \[\overline {\varepsilon_1}=\frac{1}{2}M_0\overline {v^2} \]

• 平均平动动能的压力表达：
  \[p=\frac{2}{3}n\overline {\varepsilon_1} \]

• 平均平动动能的温度表达:

\[\overline {\varepsilon_1}=\frac{3}{2}kT \]

• 由上式可知分子的平均平动动能与速率的平方的平均值成正比,与温度和压力成正比

\[方均根速率:v_{rms}=\sqrt{\overline{v^2}}=\sqrt{\frac{3kT}{m_0}}=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3p}{\rho}} \]

分子自由度

分子种类	平动自由度	转动自由度	总自由度
单原子分子\(He,Ne\)	3	0	3
双原子分子\(H_2,CO\)	3	2	5
线性多原子分子\(CO_2,C_2H_2\)	3	2	5
非线性多原子分子\(H_2O,CH_4\)	3	3	6

• 因为分子运动既有平动动能和转动动能,且各个方向上的平动和转动动能相同都为\(\frac{1}{6}M_0\overline{v^2}\)
• 理想气体内能就等于分子数N乘以单个分子的平均动能
  \[E=\frac{i}{2}vRT \]

• \(N_A\)为阿伏伽德罗常量,\(v\)为气体物质的量

麦克斯韦速率分布律

• 即不同速度段分子占总分子数的比例

\[\frac{dN_v}{N}=f(v)dv \]

• 因为麦克斯韦速率分布律是一个中间大两边小的函数,所以有三个特征速率
• 最概然速率:\(f(v)\)取到极大值时的分子速率
  \[v_p=\sqrt{\frac{2RT}{M}}\approx1.41\sqrt{\frac{RT}{M}} \]

• 平均速率:
  \[\overline v=\sqrt{\frac{8RT}{\pi M}}\approx1.60\sqrt{\frac{RT}{M}} \]

• 方均根速率:分子速率平方的平均值的平方根
  \[v_{rms}=\sqrt{\frac{3RT}{M}}\approx 1.73 \sqrt{\frac{RT}{M}} \]

理想气体分子的平均自由程

• 平均碰撞概率:一个分子单位时间内与其他分子发生碰撞的次数
• 通过单位时间走过的圆柱体内部其余分子数计算
  \[\overline Z=n\overline u \pi d^2 \]

• 平均自由程:一个分子在相邻两次碰撞剪自由运动的距离

\[\overline \lambda =\frac{\overline v}{\overline Z}=\frac{kT}{\sqrt{2}\pi d^2p} \]

热力学基础

热力学第一定律

• 准静态,相当缓慢的变化过程
• 功的数量等于机械能转化成内能的数量

体积功和热量的确定

• 在优先的准静态过程中,气体对外界所做的功
  \[W=\int_{V_1}^{V_2}pdV \]

• 设系统在准静态过程中,温度增量为dT,所传递的热量为dQ,dQ与dT成正比
  \[dQ=C_xdT \]

• \(C_x\)称为热容，即温度和热量的关系
• 摩尔定容热容:i为自由度
  \[C_{V,m}=\frac{i}{2}R \]

• 摩尔定压热容:
  \[C_{p,m}=(\frac{i}{2}+1)R \]

• 摩尔定压热容和摩尔定容热容之比,称为比热容比或者泊松比

\[\gamma =\frac{C_{p,m}}{C_{V,m}}=\frac{i+2}{i} \]

等值过程(体积,气压,温度当中有一个为定值)

• 等体过程: 体积恒定,初态\((p_1,T_1)\),末态\((p_2,T_2)\),体积功为0

\[Q=\Delta E+W=vC_{V,m}(T_2-T_1) \]

• 等压过程: 压强恒定,初态\((V_1,T_1)\),末态\((V_2,T_2)\)时

\[W=vR(T_2-T_1) \]

\[Q=vC_{p,m}(T_2-T_1) \]

• 等温过程: 温度恒定,初态\((V_1,p_1)\),末态\((V_2,p_2)\)时,内能增量为0

\[Q=W=vRTln\frac{V_2}{V_1} \]

绝热过程

• 由\(dQ=dE+dW=0,dE=vC_{V,m},dW=pdV\)可推
  \[pV^\gamma =C_4 \]
  • \(C_4\)为常量,\(\gamma\)为泊松比
  • 同理有等价方程
  \[TV^{\gamma-1}=C_4^\prime \]
  \[p^{\gamma-1}T^{-\gamma}=C_4^{\prime \prime} \]

• 由体积功可计算系统经绝热过程对外界所做的功:

\[W=\frac{1}{\gamma -a}(p_1V_1-p_2V_2) \]

\[W=-\Delta E=\frac{i}{2}vR(T_1-T_2) \]

• 特殊：绝热自由膨胀
  • 气体在真空中膨胀，不对外做功，内能不变，温度不变

热机

• 热机在循环中吸收热量\(Q_1\)，放出热量\(Q_2\)，系统对外界做功\(W_1\)，外界对系统做功\(W_2\),总对外做功\(W\)为\(p-v\)图包围的面积，即\(W_1-W_2\)
• 热机效率：

\[\eta=\frac{W}{Q_1}\times100\%=1-\frac{Q_2}{Q_1} \]

• 卡诺热机：将热机简化为两根等温线，两根绝热线

\[\eta_C=1-\frac{T_2}{T_1} \]

• 奥托循环（四冲程内燃机）:两根绝热线，两根等体线

\[\eta=1-(\frac{V_2}{V_1})^{\gamma-1} \]

• 制冷循环：热循环反向

\[e=\frac{Q_2}{W}=\frac{Q_2}{Q_1-Q_2} \]

• 卡诺循环制冷系数：

\[e_C=\frac{T_2}{T_1-T_2} \]

热力学概率 玻尔兹曼熵

• 本质就是分子在空间（包括速度空间和体积空间）中随机分布的概论
• 玻尔兹曼熵：\(\Omega\)
• 绝热自由膨胀玻尔兹曼熵变化:

\[\Delta S=vRln\frac{V_2}{V_1} \]

• 克劳修斯熵(本应是可逆过程才能使用，但可以分解过程，所以都可用)：

\[\Delta S=\int_{a(l_1)}^b\frac{\delta Q}{T} \]

• 三态转化熵变：

\[\Delta S=\int_{a(l_1)}^b\frac{d Q}{T}=\frac{Q}{T}=\frac{mc}{T} \]

• 物体升温

\[\Delta S=\int_{T_1}^{T_2}\frac{d Q}{T}=\int_{T_1}^{T_2}\frac{mc}{T}dT=mcln\frac{T_2}{T_1} \]

• 总熵变(通过压强代换可以得到其他方程)

\[\Delta S=vC_{V,m}ln\frac{T_2}{T_1}+vRln\frac{V_2}{V_1} \]

• 绝热

\[\Delta S=0 \]

振动

简谐振动基本特征及描述

基本特征

• 简谐振动表达式：

\[x=Acos(\omega t+\varphi) \]

• 由位移和速度可知振幅

\[\left\{\begin{matrix} x=Acos\varphi\\ v_0=-A\omega sin\varphi \end{matrix}\right.\]

• 消去\(\varphi\)求解可得

\[A=\sqrt{x_0^2+\cfrac{v_0^2}{\omega^2}} \]

• 周期和角速度

\[T=\frac{2\pi}{\omega} \]

• 相位\(\omega t+\varphi\)和初相\(\varphi\),由位移和速度表达式可得

\[\varphi=arctan(\frac{-v_0}{\omega x_0}) \]

• 旋转矢量描述简谐运动\(x(t)=Acos(\omega t+\varphi)\)
  

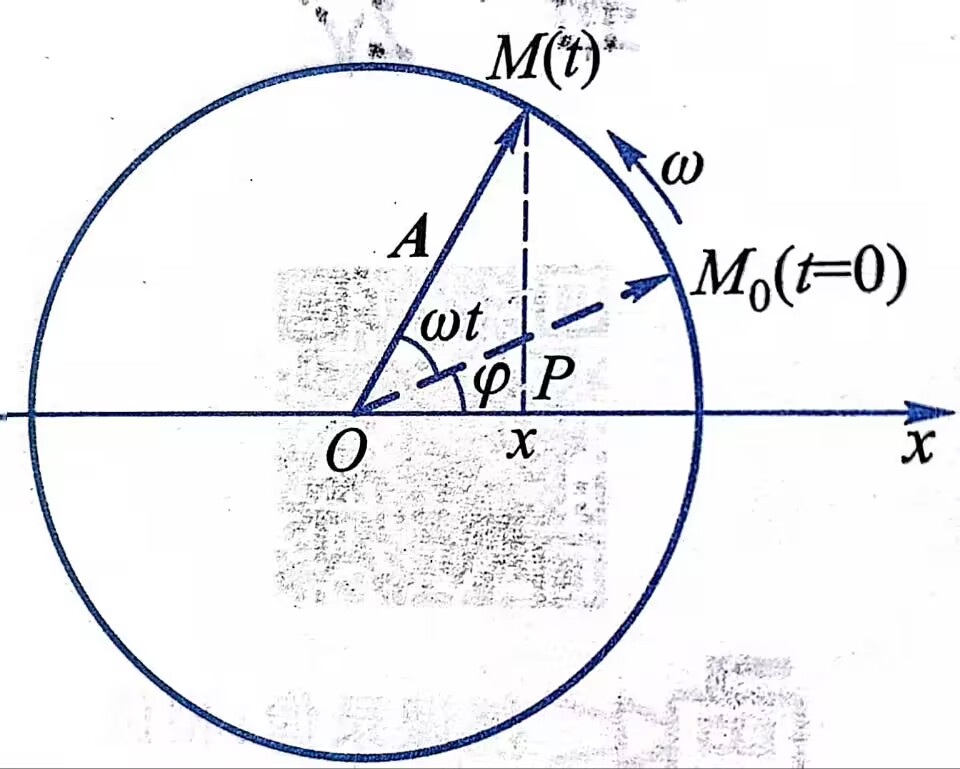
应用

• 弹簧振子：
  • 简谐运动的动力学特征

\[F=-kx \]

• 简谐运动的运动学特征

\[\left.\begin{matrix} x=Acos(\omega+\varphi)\\ a=-A\omega^2cos(\omega+\varphi) \end{matrix}\right\} \\~\\ a=-\omega^2x\]

• 简谐运动的微分方程

\[\frac{d^2x}{dt^2}+\omega^2x=0 \]

• 弹簧振子固有角频率

\[a=\frac{F}{m}=-\frac{k}{m}x \\~\\ \omega =\sqrt{\frac{k}{m}}\\~\\ T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}\]

• 角谐振子(单摆是复摆的一个特殊情况)：
  
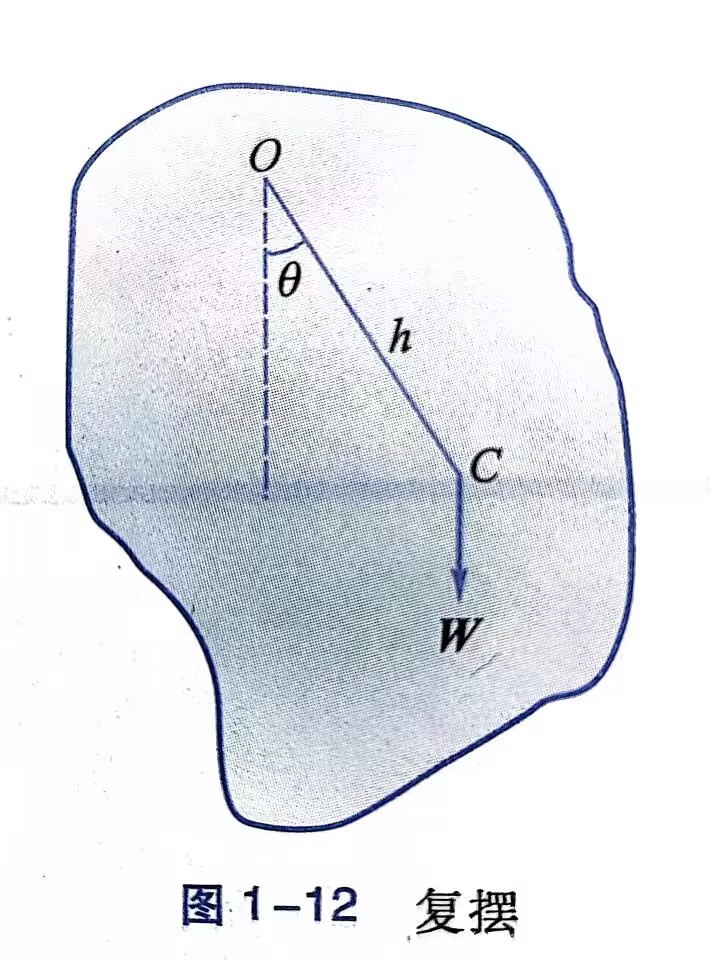
  • 角谐振动的动力学特征
  \[M=-mgh\theta \]
  • 角谐振动的运动学特征
  \[\alpha=-\omega^2\theta \]
  • 角谐振动的固有角频率
  \[\omega=\sqrt{\frac{mgh}{J}} \]
  \[T=2\pi\sqrt{\frac{J}{mgh}} \]

简谐运动的能量

\[r=\frac{1}{2}kA^2 \\~\\ E_0=\frac{1}{2}mv_0^2+\frac{1}{2}mv_1^2\]

波动

基本描述方式

• 波线：波的传播方向
• 波面：由振动相位相同的各点连成的面
• 波前：某一时刻最前的波面
• 波长\(\lambda\)：相位差为\(2\pi\)的两点之间的距离。波长的倒数记作波数或空间频率\(\sigma\)。波数的\(2\pi\)倍称为角波数\(k\)。
• 波长的周期\(T\)
• 波的频率\(v\)：周期的倒数 ps:哪个小天才想出来的用\(v\)表示
• 角频率\(\omega\)：频率的\(2\pi\)倍

\[\omega=\frac{2\pi}{T}=2\pi v \]

• 波速\(u\):波传递的速率,对于机械波，波速由传播介质决定，切变模量\(G\)(固体横波)，弹性模量\(E\)（固体纵波），体积模量\(K\)(气体液体纵波)，后面两个是理想气体中声波的传播

\[u_L=\sqrt{\frac{K}{\rho}}=\sqrt{\frac{\gamma p}{\rho}}=\sqrt{\frac{\gamma RT}{M}} \]

惠更斯原理

• 惠更斯原理：在波的传播过程中，波前上的每一点都可看作是发射子波的波源，在其后的任意时刻，这些子波的包迹就成为了新的波面。
• Todo:p42页插画
• 反射定律:\(i=i'\)
• 折射定理：

\[\frac{sin~i}{sin~\gamma}=\frac{u_1}{u_2}=n_{21} \]

简谐波

• 沿\(x\)轴正向传播的简谐波的波函数(距离原点\(x\)处质元在\(t\)时刻离开平衡位置的位移):

\[y=Acos[\omega(t-\frac{x}{u})+\varphi_0] \]

• Todo:p47插图
• 易得，波在时间上的状态变化相当于整个波形沿前进方向移动，称为行波。沿\(x\)轴正向称为右行波，负方向为左行波。
• Todo:波动方程解释
• TODO:波动动能和是能的推导

\[dE_k=dE_p=\frac{1}{2}(\rho dV)\omega ^2A^2sin^2\omega(t-\frac{x}{u}) \]

• 波动中动能和势能相等且同步变化，波动的过程就是能量传播的过程，即波是能量传播的一种形式。
• 波的平均能量密度：能量密度在一个周期内对时间的平均值

\[\overline w=\frac{1}{2}\rho\omega^2A^2 \]

• 波的能流密度:

\[I=\frac{1}{2}\omega^2A^2\rho u=\frac{E}{S} \]

• 平面简谐波在无吸收的均匀介质中传播振幅保持不变，但球面波等情况不同。

波的叠加

• 相干条件：1、频率相同。2、相位差恒定。3、振动方向一致。
• 设振动波函数:

\[y_1=A_1cos(\omega t+\varphi_{10}-2\pi\frac{r_1}{\lambda})\\~\\ y_2=A_1cos(\omega t+\varphi_{20}-2\pi\frac{r_2}{\lambda})\]

• 则合成波的强度为

\[I=I_1+I_2+2\sqrt{I_1I_2}cos~\Delta\varphi\\~\\ \Delta\varphi=\varphi_{20}-\varphi_{10}-2\pi\frac{r_2-r_1}{\lambda}\]

• 驻波：两列政府相同的相干波在同一直线上沿相反方向传播时，在叠加区域内形成的波称为���波

\[y=2Acos~\frac{2\pi}{\lambda}xcos~\omega t \]

• 波腹：振动位移\(|y|\)最大的点
• 波节：始终静止在平衡位置上的点
• 驻波不是行波，不具备行波的传播特征,在驻波场中，能量不断在波节和波腹间转移，但没有能量的定向传播
• 半波损失：光疏到光密的反射有半波损失（\(\pi\)的相位突变），光密到光疏无损失

光的干涉

• 光程：光在介质中的几何路程折射到真空中的几何路程称为光程
  \[r'=nr \]

• 可计算两列光的光程差为

\[\delta=n_2r_2-n_1r_2 \]