工数下笔记

工科数学分析下

第六章 向量代数和空间解析几何

\[向量平行条件：\frac{x_2}{x_1}=\frac{y_2}{y_1}=\frac{z_2}{z_1} \]

方向角

\[设向量\vec{a}与三个坐标轴正方向的夹角分别为\alpha,\beta,\gamma,则\alpha,\beta,\gamma称为向量\vec{a}的方向角，方向角唯一确定了方向的向量 \]

\[cos^2\alpha + cos^2\beta + cos^2\gamma =1 \]

\[a^0 = \lbrace cos\alpha,cos\beta,cos\gamma\rbrace \]

向量的乘积

向量的数量积

\[\vec a \cdot \vec b=|\vec a| |\vec b| cos\langle \vec a, \vec b \rangle \]

\[\vec a \cdot \vec b = x_1 x_2+y_1 y_2 + z_1 z_2 \]

\[cos \langle \vec a , \vec b \rangle =\frac{\vec a \cdot \vec b}{|\vec a||\vec b|}=\frac{x_1 x_2+y_1 y_2+z_1 z_2}{\sqrt{x_1^2+y_1^2+z_1^2}\sqrt{x_2^2+y_2^2+z_2^2}} \]

向量的向量积

\[\vec a\times \vec b 同时垂直于\vec a和\vec b ，且\vec a,\vec b, \vec a \times \vec 成右手系 \]

\[|\vec a \times \vec b|=|\vec a||\vec b|sin\langle \vec a,\vec b \rangle ,即\vec a,\vec b 构成的平行四边形的面积 \]

\[\vec a //\vec b <=>|\vec a \times \vec b|=0 \]

\[ \vec a \times \vec b= \begin{vmatrix} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{vmatrix} \]

向量的混合积

\[ (\vec a,\vec b,\vec c)=(\vec a \times \vec b) \cdot \vec c = \begin{vmatrix} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \\ \end{vmatrix}=以\vec a,\vec b,\vec c为底的平行六面体的面积,且 \vec a,\vec b,\vec c三者互换位置不影响\]

\[三向量\vec a,\vec b,\vec c共面<=>(\vec a,\vec b,\vec c)=0 \]

平面的方程

点法式

\[给定点M_0(x_0,y_0,z_0)和一个非零向量\vec n=\lbrace A,B,C\rbrace,存在唯一一个平面过点M_0且与\vec n 垂直 \]

\[A(x-x_0)+B(y-y_0)+C(z-z_0)=0 \]

平面的一般方程

\[Ax+By+Cz+D=0 ,\vec n=\lbrace A,B,C\rbrace 即为平面法向量 \]

截距式

\[设平面与x轴，y轴，z轴的交点为M_1(a,0,0),M_2(0,b,0),M_3(0,0,c),则平面方程为 \]

\[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 \]

有关平面的一些问题

两平面的夹角

\[\pi_1=A_1x+B_1y+C_1z+D_1=0 法向量为\vec{n_1} \]

\[\pi_2=A_2x+B_2y+C_2z+D_2=0 法向量为\vec{n_2} \]

\[cos\theta =\frac{|\vec{n_1}\cdot \vec{n_2}|}{|\vec{n_1}||\vec{n_2}|}=\frac{|A_1 A_2+B_1B_2+C_1C_2|}{\sqrt{A_1^2+B_1^2+C_1^2}\sqrt{A_2^2+B_2^2+C_2^2}} \]

点到平面的距离

\[M_0:(x_0,y_0,z_0) \]

\[\pi:Ax+By+Cz+D=0 \]

\[d=\frac{|Ax_0+By_0+Cz_0+D|}{\sqrt{A^2+B^2+C^2}} \]

平面束

\[ \left\{ \begin{aligned} \pi_1=A_1x+B_1y+C_1z+D_1=0 \\ \pi_2=A_2x+B_2y+C_2z+D_2=0 \end{aligned} \right.\]

\[过两平面交点的平面：\mu(A_1x+B_1y+C_1z+D_1)+\lambda(A_2x+B_2y+C_2z+D_2)=0 \]

\[可和\pi_1重合但不和\pi_2重合： (A_1x+B_1y+C_1z+D_1)+\lambda(A_2x+B_2y+C_2z+D_2)=0 \]

空间直线方程

直线的一般方程

\[A_1x+B_1y+C_1z+D_1=0 \]

\[A_2x+B_2y+C_2z+D_2=0 (A_1:B_1:C_1)\neq(A_2:B_2:C_2) \]

直线的标准方程和参数方程

\[设M_0(x_0,y_0,z_0)是空间中一点，\vec s=\lbrace l,m,n\rbrace ，则唯一存在一条直线L过点M_0且与\vec s平行 \]

\[标准方程或对称式方程：\frac{x-x_0}{l}= \frac{y-y_0}{m}= \frac{z-z_0}{n} \]

\[ 参数方程： \left\{ \begin{aligned} x=x_0+lt \\ y=y_0+mt\\ z=z_0+nt \end{aligned} \right.\]

有关直线和平面的一些问题

直线与直线的夹角

\[L1:\frac{x-a_1}{l_1}=\frac{y-b_1}{m_1}=\frac{z-c_1}{n_1} 设\vec {s_1}={l_1,m_1,n_1} \]

\[L2:\frac{x-a_2}{l_2}=\frac{y-b_2}{m_2}=\frac{z-c_2}{n_2} 设\vec {s_2}={l_2,m_2,n_2} \]

\[cos\theta=\frac{|\vec {s_1}\cdot\vec {s_2}|}{|\vec {s_1}||\vec{s_2}|} =\frac{|l_1 l_2+m_1m_2+n_1n_2|}{\sqrt{l_1^2+m_1^2+n_1^2}\sqrt{l_2^2+m_2^2+n_2^2}} \]

直线与平面夹角

\[L:\frac{x-a}{l}= \frac{y-b}{m}= \frac{z-c}{n} \]

\[\pi:Ax+By+Cz+D=0 \]

\[sin\theta=\frac{|\vec s\cdot \vec n| }{|\vec s||\vec n|}=\frac{|lA+mB+nC|}{\sqrt{l^2+m^2+n^2}\sqrt{A^2+B^2+C^2}} \]

点到直线的距离

• 过点作垂面，求垂面与直线的交点，求两点距离
• 在L上任取一点，求两点构成的向量在直线上的投影，解三角形
• 在L上任取一点，求两点构成的向量和直线向量的向量积，解平行四边形
• 设直线上的点，求两点距离，取最小值

两线共面

• 两条线各取一点，构成向量，与原直线共三个向量，求三向量共面即可

空间曲面和空间曲线

曲面方程

\[ F(x,y,z)=0 \\ 或 \\ \left\{ \begin{aligned} x=x(u,v), \\ y=y(u,v), \\ z=z(u,v) \end{aligned} \right. \]

1.旋转曲面:转谁谁不变，将另一个参数变成到轴的距离

\[ F(x,y)=0 \\绕y轴旋转得 \\ F(\pm \sqrt{x^2+y^2},y)=0 \]

2.曲面在坐标面上投影���解,在方程中将带投影面的坐标消去即可
3.柱坐标系:坐标代换

\[ \left\{ \begin{aligned} x=\rho cos \theta \\ y=\rho sin \theta \\ z =z \end{aligned} \right. \]

4.球坐标系:坐标代换

\[ \left\{ \begin{aligned} x=rcos \theta sin\varphi \\ y=r sin \theta sin\varphi \\ z =rcos\varphi \end{aligned} \right. \]

常见曲面

1.柱面：一直线沿给定曲线平行移动所形成的曲面S，曲线叫做准线，直线叫做母线

\[ C:\left\{ \begin{aligned} F(x,y)=0 \\ z=0 \end{aligned} \right. \\或 \\ F(x,y)=0 \]

2.椭圆锥面

\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=\frac{z^2}{c^2} \]

3.椭球面

\[\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1 \]

4.单叶双曲面

\[\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1 \]

5.双叶双曲面

\[\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=-1 \]

6.椭圆抛物面

\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=z \]

7.双曲抛物面

\[\frac{x^2}{a^2}-\frac{y^2}{b^2}=-z \]

第七章 多元函数微分学

二元函数

• 二元函数的定义是平面上的点集
• 二元函数的定义域通常是一条或几条曲线���成的一部分平面，这样的点集被称为区域，围成区域的曲线被称为区域的边界。如果区域包含边界，则称为闭区域，反之称为开区域。

多元函数的极限

• P(x,y)以不同的曲线方式（如\(x=y或x=y^2\)）趋于\(P_0(x_0,y_0)\)时，函数趋于相同的值则极限\(\lim_{x\rightarrow + \infty y\rightarrow + \infty} f(x,y)\)不存在

多元函数的连续性

• 多元初等函数在其定义域上是连续的
• 同一元函数

偏导数

定义

• 设函数\(z=f(x,y)\)在点\((x_0,y_0)\)的某邻域内有定义，将\(y\)固定在\(y_0\),而\(x\)在\(x_0\)处取得增量\(\Delta x\)时，函数$f(x,y) $所产生的响应的增量称为偏增量

\[\Delta _x z=f(x_0+\Delta x,y_0)-f(x_0,y_0) \]

• 如果极限

\[\lim_{\Delta x\rightarrow 0} \frac{\Delta _x z}{\Delta x}=\lim_{\Delta x\rightarrow 0} \frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x} \]

存在则称此极限为函数$ z=f(x,y)$ 在点\((x_0,y_0)\)处对$ x$的偏导数，记作

\[\left. \frac{\partial z}{\partial x} \right | _{(x_0,y_0)}, \left. \frac{\partial f}{\partial x} \right | _{(x_0,y_0)},\left. z^\prime _x \right | _{(x_0,y_0)},f^\prime _x (x_0,y_0),f^\prime _1 (x_0,y_0) \]

• 偏导数是一个整体,不能像倒数一样拆分即

\[\frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial y} \neq \frac{\partial z}{\partial y} \]

高阶偏导数

• 如果函数 $ z=f(x,y) $ 的两个混合的偏函数\(f^{\prime\prime} _{xy}(x,y)\)与\(f^{\prime\prime} _{yx}(x,y)\)在区域D内连续,则在此区域内必有

\[f^{\prime\prime} _{xy}(x,y)= f^{\prime\prime} _{yx}(x,y) \]

全微分

• 函数存在<函数连续<函数偏导数存在<函数全微分存在<函数偏微分连续
• 如果函数\(z=f(x,y)\)在点\((x,y)\)的全增量可表示为$$\Delta z=A\Delta x+B\Delta y +o(\rho),\rho=\sqrt{\Delta x^2+\Delta y^2} $$
• 则\(A\Delta x+B\Delta y\)被称为函数在点\((x,y)\)的全微分,记作\(dz\)或\(df\)
  \[dz=A\Delta x+B\Delta y=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy \]

• 应用
  • 近似计算
  \[f(x,y)=f(x_0,y_0)+\frac{\partial f}{\partial x}(x-x_0)+\frac{\partial f}{\partial y}(y-y_0) \]
  • 误差估计(和近似计算差不多,加个绝对值就行,误差总不能是负的)

复合函数求导

• 通过函数结构图求解
  • 设\(u=f(x,y,z),x=\varphi(s,t),z=g(s)\)
  \[\frac{\partial u}{\partial s}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial s}+\frac{\partial u}{\partial z}\frac{\partial z}{\partial s} \]
  \[\frac{\partial u}{\partial t}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial t} \]

• 求多阶导
  • 通过全微分形式的不变性,即设\(z=f(u,v)\),不论\(u,v\)是中间变量还是自变量,它的全微分形式总可以写成
  \[dz=\frac{\partial z}{\partial u}du+\frac{\partial z}{\partial v}dv \]

隐函数求导法

• 由一个方程确定的隐函数(上下相反)
  • 如果函数\(F(x,y)\) 在点\(P(x_0,y_0)\)上有连续的偏导数，且\(F(x_0,y_0)=0,F^`_y(x_0,y_0)\neq 0\),则方程\(F(x,y)=0\)在点\((x_0,y_0)\)的某邻域内有唯一确定的一个隐函数\(y=f(x)\)
  \[\frac{dy}{dx}=-\frac{F^\prime_x}{F^\prime_y} \]
  • 如果函数是三元隐函数，\(F(x,y,z)=0\)
  \[\frac{\partial z}{\partial x}=-\frac{F^\prime_x}{F^\prime_z}，\frac{\partial z}{\partial y}=-\frac{F^\prime_y}{F^\prime_z} \]

• 由方程组确定的隐函数
  • 若是三元函数，则可通过同时对x求偏导，得到两个导数的关系式，通过关系式求解
  • 设函数\(F(x,y,u,v)=0,G(x,y,u,v)=0\)，在点\(P(x_0,y_0,u_0,v_0)\)有连续偏导数，且雅可比行列式存在
  \[J=\frac{\partial (F,G)}{\partial (u,v)}= \begin{vmatrix} F^\prime_u & F^\prime_v \\ \\ G^\prime_u & G^\prime_v \\ \end{vmatrix}\]
  • 雅可比行列式不等于0则存在
  \[\frac{\partial u}{\partial x}=\frac{\frac{\partial (F,G)}{\partial (x,v)}}{\frac{\partial (F,G)}{\partial (v,u)}}，\frac{\partial v}{\partial x}=\frac{\frac{\partial (F,G)}{\partial (x,u)}}{\frac{\partial (F,G)}{\partial (u,v)}} \]

方向导数和梯度

• 方向导数：沿向量\(\vec l\)方向的导数
  • 定义法：求极限
  \[\frac{\partial z}{\partial l}=\lim_{\rho \rightarrow 0} \frac{\Delta _l z}{\rho} \]
  • 若函数在带点附近可微且方向导数都存在,\(e\)：
  \[\frac{\partial z}{\partial l}=\frac{\partial z}{\partial x}cos\alpha +\frac{\partial z}{\partial y}cos\beta \]

• 梯度：最大的方向导数
  \[gradz= \begin{Bmatrix}\frac{\partial z}{\partial x},\frac{\partial z}{\partial y} \end{Bmatrix}\]

空间曲线的切线和法平面

• 若曲线方程为
  \[x=x(t) ,y=y(t),z=z(t) \]
  \[\vec s=\begin{Bmatrix}x^\prime(t_0),y^\prime(t_0),z^\prime(t_0) \end{Bmatrix} \]

• 若曲线方程为
  \[\left\{ \begin{aligned} F(x,y,z)=0 \\ G(x,y,z)=0 \end{aligned} \right.\]
  则函数在点\(P_0(x_0,y_0,z_0)\)的切向量为
  \[s=\lbrace 1,\left. \frac{\partial y}{\partial x} \right |_{P_0},\left. \frac{\partial z}{\partial x} \right |_{P_0}\rbrace或s=\lbrace dx,dy,dz \rbrace \]

• 将\(A(t)=\lbrace x(t),y(t),z(t) \rbrace\)称为向量函数
  \[(A\cdot B)^\prime=A^\prime\cdot B+A\cdot B^\prime \\ ~ \\ (A\times B)^\prime=A^\prime\times B+A\times B^\prime\]

• \(A(t)\)的积分即是各个方向上的积分之和
• 曲线的切平面的法向量即是梯度方向

二元函数的泰勒公式

\[\begin{aligned} f(a+h,b+k) =& f(a,b) + hf^\prime_x(a,b) + kf^\prime_y(a,b) \\ &+ \frac{1}{2} (h^2f^\prime_{xx} + 2hkf^\prime_{xy} +k^2f^\prime_{yy}) \end{aligned} \\ \]

拉格朗日余项：

\[R_2=\frac{1}{3!} \sum_{i=0}^{3} C^r_3 \frac{\partial^3f(x_0+\theta h,y_0+\theta k)}{\partial x^r \partial y^{3-r}}(0<\theta <1) \]

皮亚诺余项：

\[o(\rho ^2) \]

多元函数的极值（泰勒公式推导）

• 可疑点（可能的极值点）要么是边界值，要么导数为零，即\(f^\prime_x(x_0,y_0)=0,f^\prime_y(x_0,y_0)=0\)
• 记\(f^{\prime\prime}_{xx}(x_0,y_0)=A,f^{\prime\prime}_{xy}(x_0,y_0)=B,f^{\prime\prime}_{yy}(x_0,y_0)=C\)
  • 当\(AC-B^2>0\),且\(A<0\)时，\(f(x_0,y_0)\)是极大值
  • 当\(AC-B^2>0\),且\(A>0\)时，\(f(x_0,y_0)\)是极小值
  • 当\(AC-B^2<0\),不是极值
  • 当\(AC-B^2=0\),另行讨论
• 条件极值：
  • 设目标函数为\(z=f(x,y)\)，约束条件为\(\varphi(x,y)=0\)
  • 若\((x_0,y_0)\)是条件极值点，则一定是下列方程的解
  \[\left\{ \begin{aligned} f^\prime_x(x,y)+\lambda\varphi^\prime_x(x,y)=0 \\ f^\prime_y(x,y)+\lambda\varphi^\prime_y(x,y)=0 \\ \varphi(x,y)=0 \end{aligned} \right.\]

第八章 重积分

二重积分

• 就是对某个维度积分后，再在其他维度进行积分。
• 表现形式:

\[\iint\limits_D f(x,y)d\sigma \]

\[\int _c^ddx\int_{x_1(y)}^{y_2(x)}f(x,y)dy \]

• 极坐标中的二重积分表示

\[\iint\limits_Df(x,y)d\sigma =\iint\limits_Df(\rho cos\theta ,\rho sin\theta)\rho d\theta d\rho \]

\[\int_\alpha^\beta d\theta\int_{\rho_1(\theta)}^{\rho_2(\theta)}(\rho cos\theta ,\rho sin\theta)\rho d\rho \]

三重积分

• 基本同二重积分
• 球坐标系中的三重积分：

\[\iiint\limits_Vf(x,y,z)dV=\iiint\limits_Vf(rcos\theta sin\varphi,rsin\theta sin\varphi,rcos\varphi)r^2sin\varphi dr d\varphi \]

\[=\int_\alpha^\beta d\theta\int_{\gamma}^{\tau}sin\varphi d\varphi\int_{\tau_1(\varphi)}^{\tau_2(\varphi)}f(rcos\theta sin\varphi,\tau sin\theta sin\varphi,\tau cos\varphi)r^2 d\tau \]

重积分的应用

• 曲面的面积:

\[A=\iint\limits_{D_{xy}}\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2} \]

• 质心:求哪一个方向就乘以哪个方向

\[\overline x =\frac{1}{M}\iiint\limits_Vx\mu(x,y,z)dV=\frac{\iiint\limits_Vx\mu(x,y,z)dV}{\iiint\limits_V\mu(x,y,z)dV} \]

• 转动惯量

\[I_L=\iiint\limits_Vd^2(Q，L)\mu(x,y,z)dV \]

• 引力

\[F_x=\iiint\limits_V\frac{Gm(x-a)\mu(x,y,z)}{r^3}dV \]

重积分换元法及含参变量的积分

• 重积分换元法(这里的\(J\)要取绝对值)

\[\iint\limits_Df(x,y)dxdy=\iint\limits_{D^\prime}f(x(u,v),y(u,v))|J|dudv \]

• 含参变量的积分
• 连续性:

\[\lim\limits_{y\rightarrow y_0}\int^b_af(x,y)dx=\int^b_a\lim\limits_{y\rightarrow y_0}f(x,y)dx \]

• 可导性:

\[F^\prime(y)=\frac{d}{dy}\int^b_af(x,y)dx=\int^b_af^\prime_ydx \]

• 积分次序交换性:如果\(f(x,y)\)在区域\(D:a\leq x\leq b,c\leq y \leq d\)上连续,可交换前后积分位置,用于转换累次积分解题

\[\int^d_cdy\int^b_af(x,y)dx=\int^b_adx\int^d_cf(x,y)dy \]

• 参数积分方程求导:对\(F(y)=\int^{\varphi_2(y)}_{\varphi_1(y)}f(x,y)dx\)

\[F^\prime(y)=\int^{\varphi_2(y)}_{\varphi_1(y)}f^\prime(x,y)dx+f(\varphi_2(y),y)\varphi^\prime_2(y)-f(\varphi_1(y),y)\varphi^\prime_1(y) \]

第九章 曲线积分与曲面积分

第一类曲线积分

• 基本形式：一般弧积分\(\int_Lf(x,y,z)dl\)，闭曲线弧积分，\(\oint_Lf(x,y,z)dl\)
• 曲线积分的计算：(个人理解是上学期曲线积分的延伸)

\[\int_Lf(x,y,z)dl=\int^\beta_\alpha f(x(t),y(t),z(t))\sqrt{[x^\prime(t)]^2+[y^\prime(t)]^2+[z^\prime(t)]^2}dt \]

第二类曲线积分

• 基本形式：相量在曲线上的积分计算（功?）

\[\int_LXdx+Ydy=\int^\beta_\alpha [X(x(t),y(t))x^\prime(t)+Y(x(t),y(t))y^\prime(t)]dt \]

• 两类曲线积分的关系:(相量的累计就是在各个坐标上投影的累计合)

\[\int_LXdx+Ydy+Zdz=\int_L(Xcos\alpha+Ycos\beta+Zcos\gamma)dl \]

格林公式

• 平面区域：连通（一坨），非连通（两坨），单连通（实心），复连通（空心）
• 格林定理：设\(D\)是平面有界单连通区域，且函数在\(D\)有一阶连续偏导数，\(L\)是其边界曲线，有

\[\oint_{L_1^+}Xdx+Ydy=\iint\limits_D(\frac{\partial Y}{\partial x}-\frac{\partial X}{\partial y}dxdy) \]

• 格林公式的图形意义：将曲线区域微分为矩形堆积而成，对矩形求积分，即可得曲线边缘的积分值
• 格林公式的物理意义：对于内部不存能量的区域，从边缘上放出的能量等于内部所有区域释放的能量之和
• 注：格林公式的使用条件只要是连通区域即可
• 格林公式计算面积：

\[A=\iint\limits_Ddxdy=\frac{1}{2}\oint_{L^+}xdy-ydx \]

• 特殊情况：路径无关
  • 函数沿任意曲线到达同一个点的值恒定

\[\oint_{L_1^+}Xdx+Ydy=0 <=> \frac{\partial Y}{\partial x}\equiv\frac{\partial X}{\partial y} \]

• 全微分：
  • 意义：已知平面函数的全微分是\(Xdx+Ydy\)，试图使\(Xdx+Ydy\)回退为\(u(x,y)\)
  • 充要条件:\(\cfrac{\partial Y}{\partial x}\equiv\cfrac{\partial X}{\partial y}\)
  • 表达式：
  \[u(x,y)=\int_{(x_0,y_0)}^{(x,y)}Xdx+Ydy+C \]
  \[\int_{(x_1,y_1)}^{(x_2,y_2)}Xdx+Ydy=u(x_2,y_2)-u(x_1,y_1) \]
  • 求解方式：折线求解
    

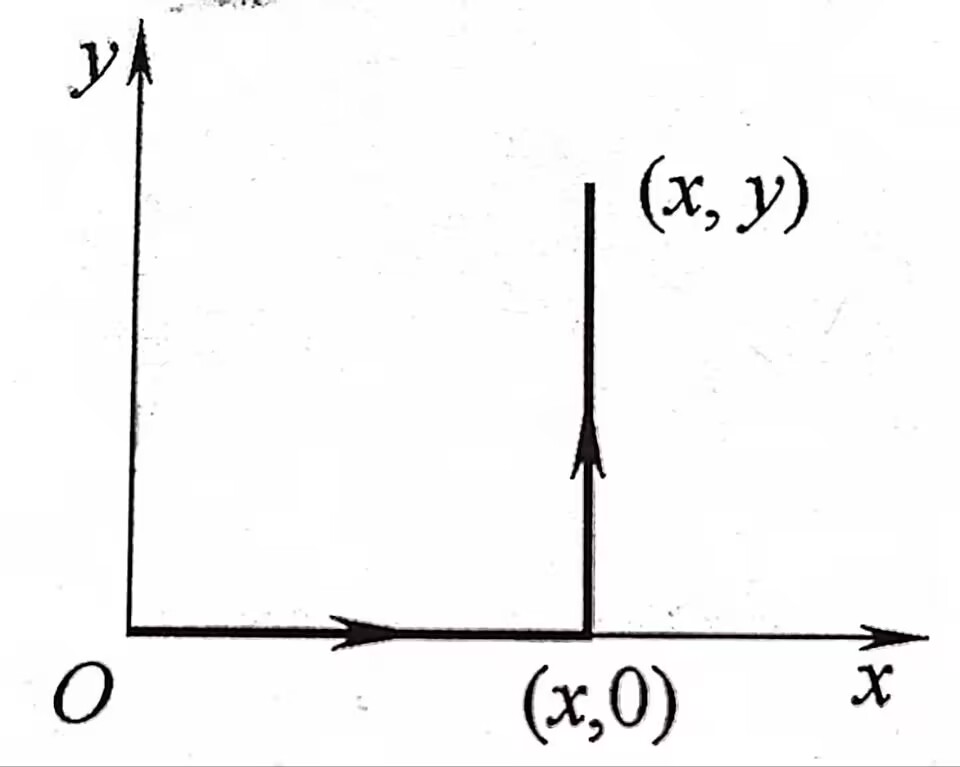
\[u(x,y)=\int_0^xX(x,0)dx+Y(x,y)dy+C \]

第一类曲线积分

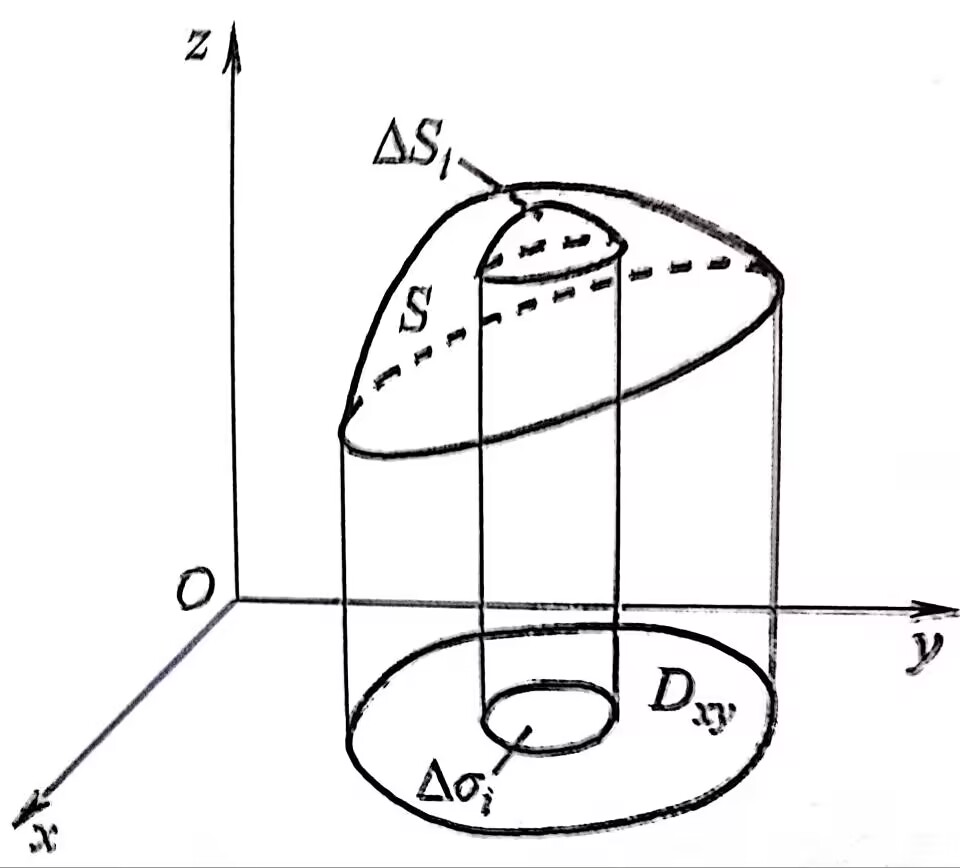
• 求解方式：把曲面投影到平面，对微小平面对应的曲面进行积分

\[\iint\limits_Sf(x,y,z)dS=\iint\limits_{D_{xy}}f(x,y,z(x,y))\sqrt{1+(\frac {\partial z}{\partial x})^2+(\frac {\partial z}{\partial y})^2}dxdy\]

+