快速傅里叶变换原理介绍及递归代码实现
快速傅里叶变换是离散傅里叶变换的一种快速实现方式,快速傅里叶变换可用于多项式乘法、大数乘法、卷积等操作,把原本的O(n^2)计算量优化到了O(nlogn),这是质的飞跃。我们现在能这么快的网上冲浪,这个算法居功至伟,让我们为它鼓掌!
O(n^2)和O(nlogn)的差距在哪里,这里的log底数是2。
如果要处理一万个数据,O(n^2)需要计算一亿次,O(nlogn)则仅需要计算十三万次。
接下来,下面我们会看到快速傅里叶变换是如何一步步地将O(n^2)优化到O(nlogn)的。
暴力破解法
根据上一篇文章所述,离散傅里叶公式如下:
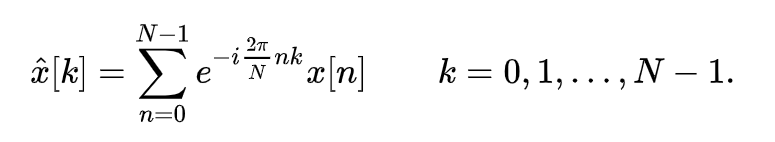
举个例子,当N为4的时候,离散傅里叶变换的运算相当于如下矩阵乘积:
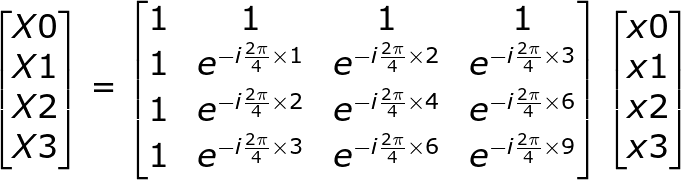
按照这个操作,我们也可以实现N*N操作的离散傅里叶变换代码。
#include<cmath>
#include<iostream>
#include<complex>
#include<vector>
using namespace std;
const double pi = acos(-1.0);
vector<complex<double>> fft(vector<complex<double>> input)
{
vector<complex<double>> output;
int N = input.size(), k = 0, n = 0;
for (k = 0; k < N; k++)
{
complex<double> sum(0,0);
for (n = 0; n < N; n++)
{
complex<double> wn(polar<double>(1, -2*pi/N * n * k));
sum += input[n] * wn;
}
output.push_back(sum);
}
return output;
}
int main()
{
vector<complex<double>> in{1, 2, 3};
auto re = fft(in);
for (auto i: re)
{
cout << "real:" << i.real() << " imag:" << i.imag() << endl;
}
return 0;
}
离散傅里叶变换运算有两层for循环,时间复杂度是O(n^2)。
从上面那张矩阵图可以看到,公式的
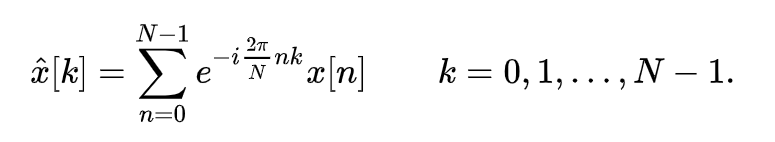
这个$$ e^{-i2\pi } $$ 是固定不变的,变化的只有N, n, k。
再此多说一句:$$ e^{-i2\pi } $$是顺时针旋转一周的意思。同理如下图的$$ e^{i\pi } $$ 也就是逆时针旋转半周的意思。
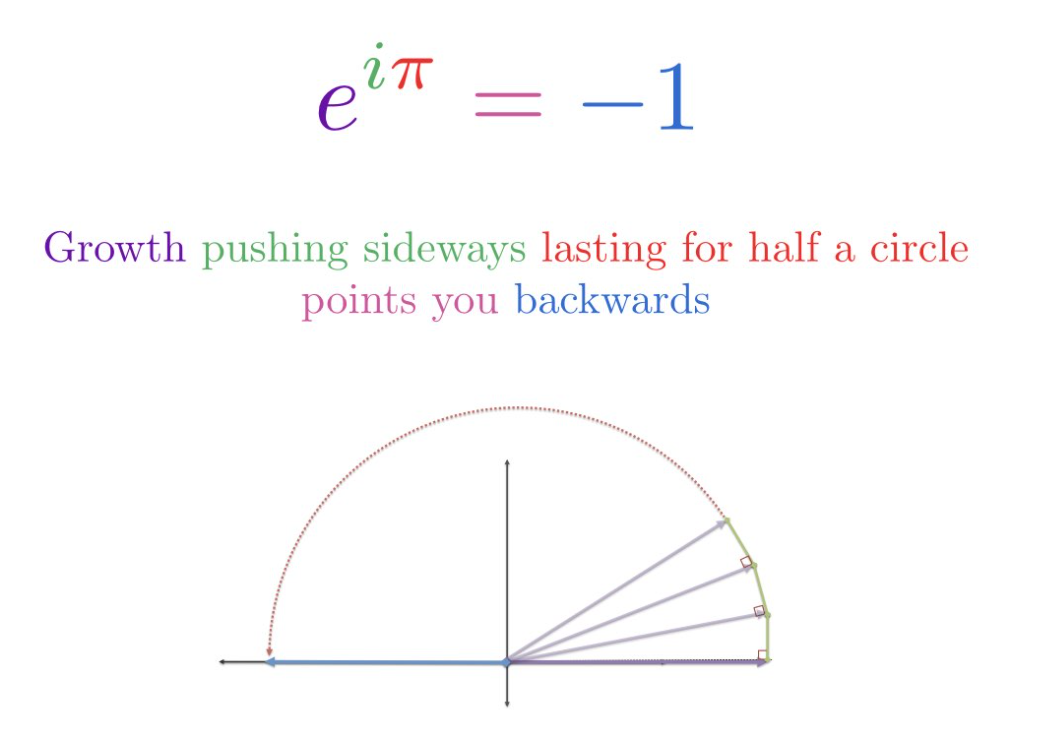
至于旋转就是这么转,这么地转动:
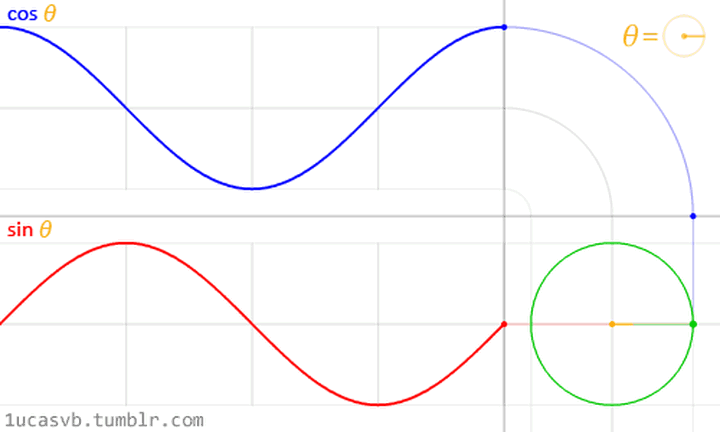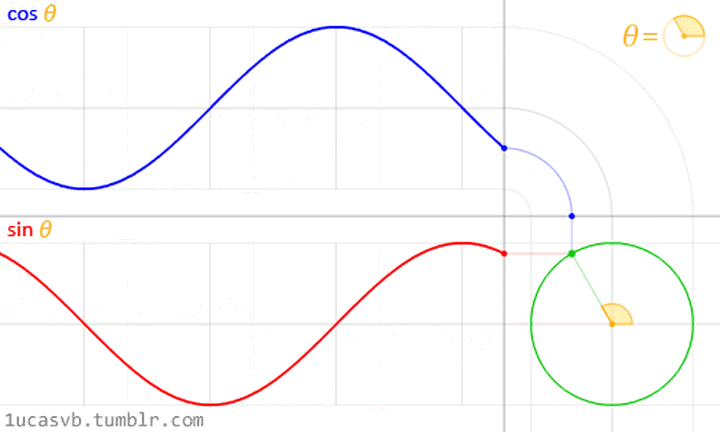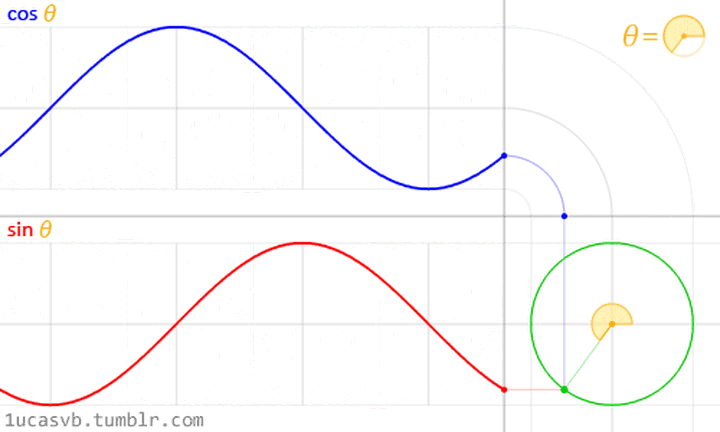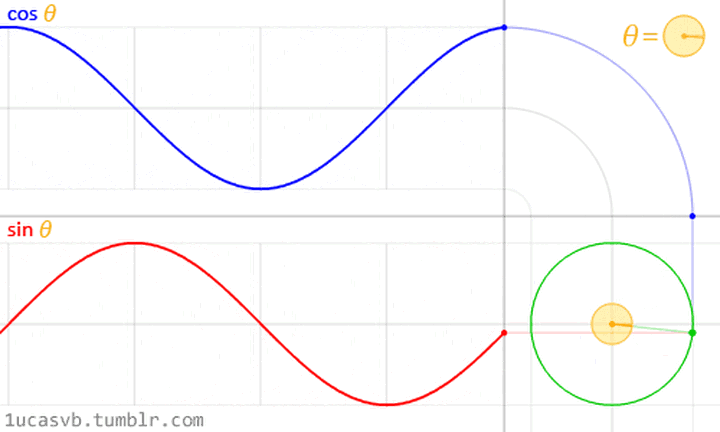
我们可以将$$ e^{-i2\pi } $$简化表示成$$ \omega $$,并将N作为下标,且nk作为上标如:$$ \omega_{N}^{nk} $$
如果$$ \omega $$代表顺时针旋转一周,那么$$ \omega_{N}^{nk} $$就代表,其步进值是顺时针旋转N分之一周,且步进次数是n*k次后的结果。
每一次旋转的步进值就是单位复数根:
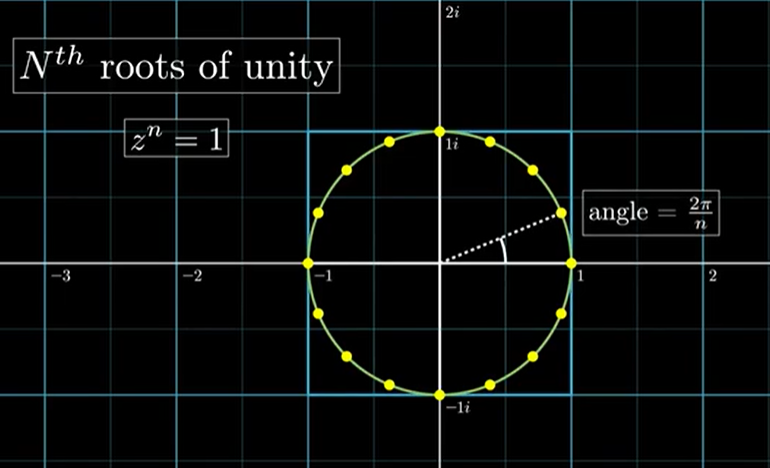
还是当N为4的时候举个例子,运算矩阵如下:
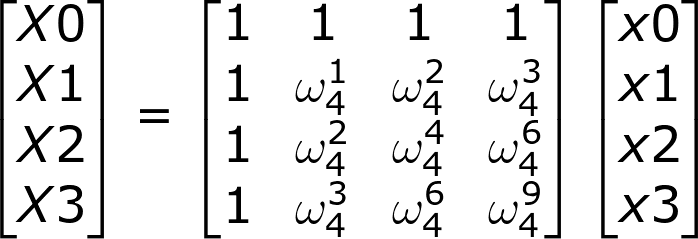
命运轮回,上述的ω再怎么变,也跳不出下图这四个红点:

而当N为2时,ω再怎么变,也跳不出下图这两个红点:

旋转定理
此时我们可以得到这样的定理。
定理一
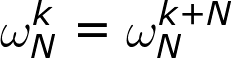
这是旋转的周期性决定,旋转一周就等于没有旋转。
定理二
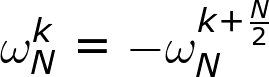
当N为偶数的时候,圆的每个点都即为X轴对称,也为Y轴对称。
定理三
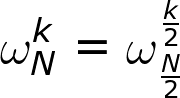
以上,当N、k均为偶数时,当N为之前的一半的时候,单位复数根也增大了一倍,所以是成立的。
根据定理一二三,我们可以把矩阵从这样:
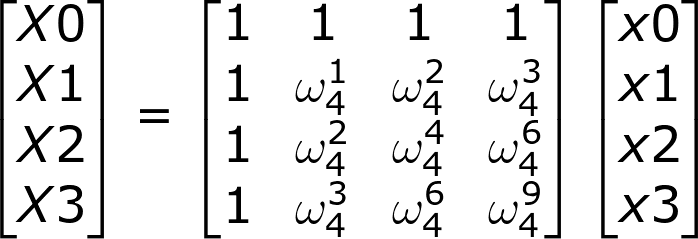
转换成这样:

看这里的时候不必过分追究细节,具体推导在下面。
我们好像看到了一些东西,似乎我们只需要求得 $$ \omega _{2}^{1} $$ 和 $$ \omega _{4}^{1} $$ 即可?
进一步可以转换成这样:
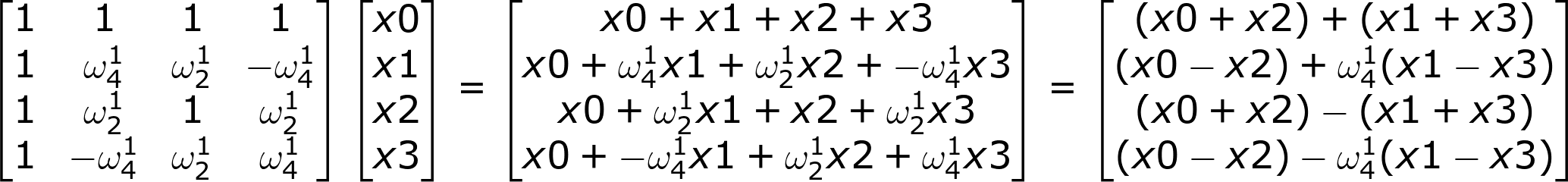
嗯?好像看到了一点规律的感觉,当我们转换一个N=4的序列的时候,我们似乎可以将它分成两个N=2的序列,各自进行转换。但是为什么会这样?
推导过程如下(也可以直接拉到最后看结论),以下参考罗博士的推导,我重新写了公式。考虑一个4点DFT,其原始公式是:
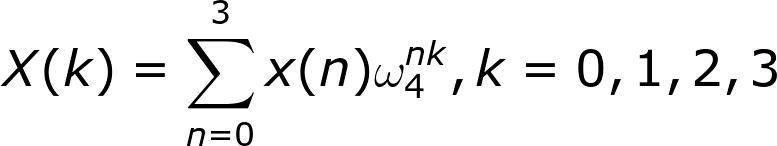
奇偶下标项拆分一下:
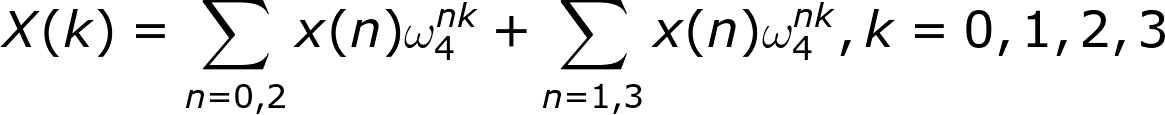
提取公共项:
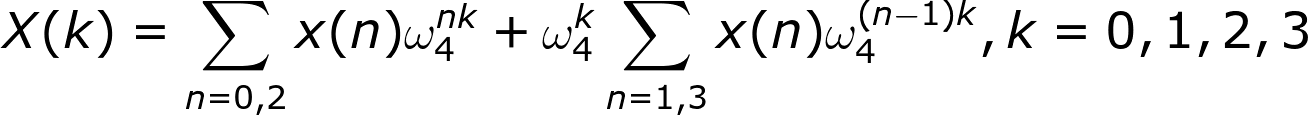
统一一下求和符号的下标n:
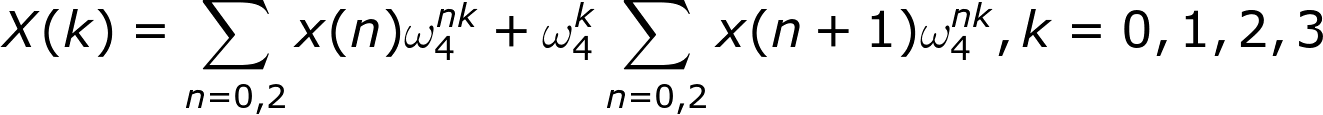
注意到N=4为偶数,根据单位复根的定理三,可以做一个比例变换,得到:

再对求和符号的下标做一个变换:
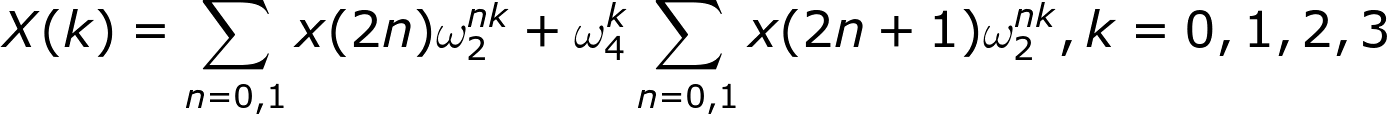
拆分成0,1和2,3:
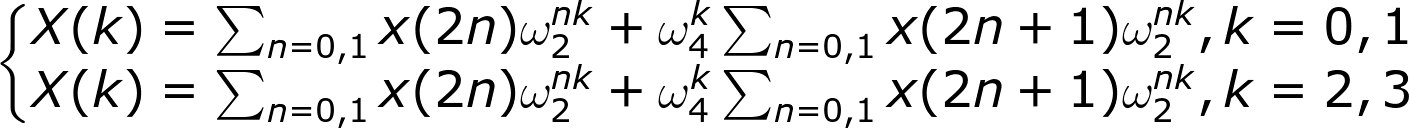
其中k=2,3项可以转换成以下公式:

根据定理一和定理二可以转换成以下公式:
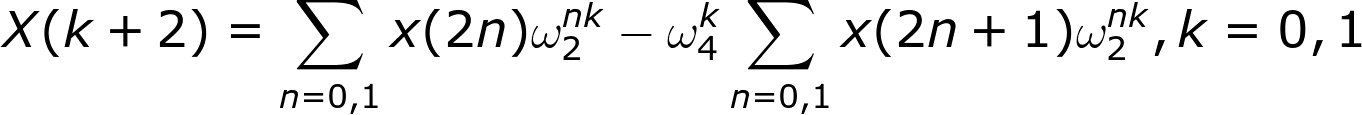
最终得到前后半部分的公式:

可以看到,如果把N=4的序列分成,偶数下标项和奇数下标项两部分,分别做FFT得到A和B,那么N=4的序列的傅里叶变换的结果:
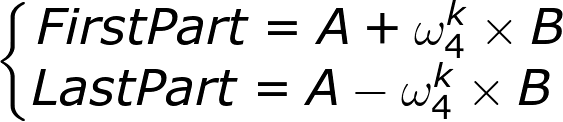
这个时候再看看之前的这个矩阵,好像有点意思:
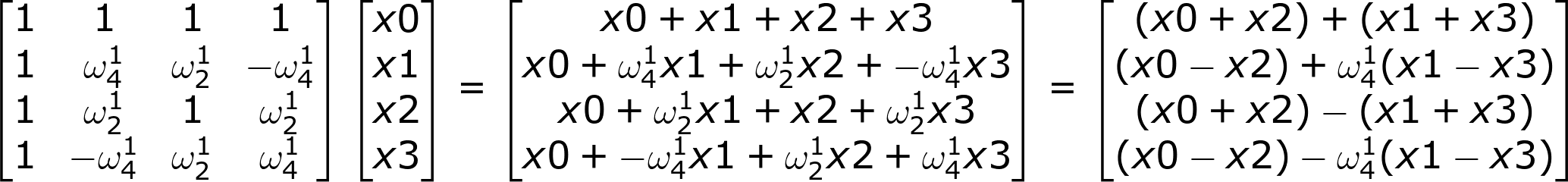
这里为了加深理解,加上X0和X2,当N=2时的FFT如下:
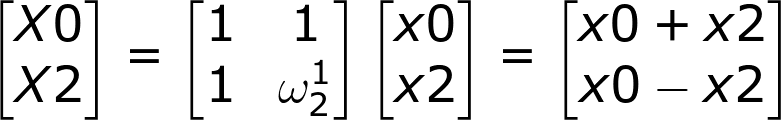
递归法(自顶向下)
如果是这样的话,原本之前我们的时间复杂度是O(N^2),现在变成了O(N*N/2)。
进一步,如果N的长度是2次幂的话,那么这个不断拆分偶数和奇数下标项的过程可以一直递归下去。
例如,如果要计算一个N=8的序列,那么拆分成两个N=4的序列计算,再拆分成四个N=2的序列计算,再拆分八个N=2的序列计算,是不是有一点归并排序的感觉了?
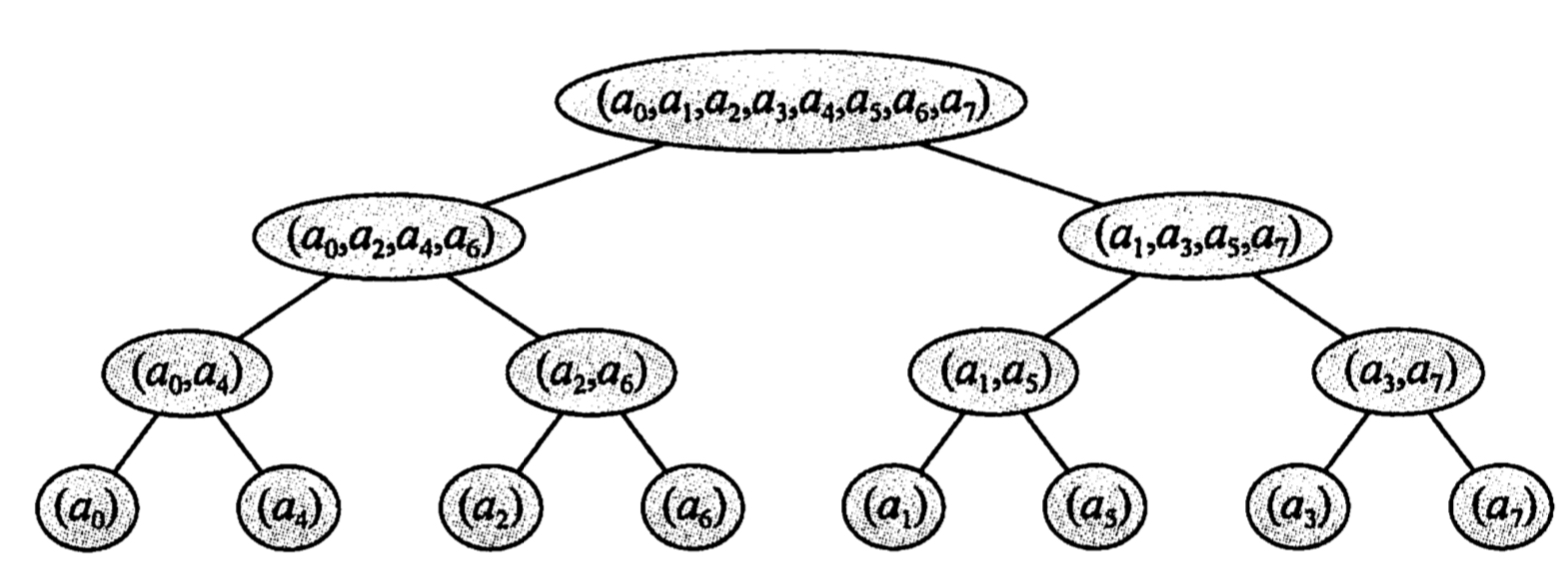
那么最终计算量可以降低到O(N*logN)
void FFT_recursion(vector<complex<double>> &input)
{
int n = input.size();
if(n == 1)
return;
int mid= input.size()/2;
vector<complex<double>> A0, A1;
for(int i = 0; i < n; i += 2){//拆分奇偶下标项
A0.push_back(input[i]);
A1.push_back(input[i + 1]);
}
FFT_recursion(A0);
FFT_recursion(A1);
complex<double> w0(1,0);
complex<double> wn(polar<double>(1, -2*pi/n));//单位根
for(int i=0; i < mid; i++, w0*=wn){//合并多项式
input[i] = A0[i] + w0*A1[i];
input[i + mid] = A0[i] - w0*A1[i];
}
}
以上我们明白了优化的思路,上述代码虽然时间复杂度降到了O(nlogn),但是空间复杂度也是O(nlogn)。下一篇将介绍时间复杂度O(nlogn),同时空间复杂度为O(1)的操作……


 浙公网安备 33010602011771号
浙公网安备 33010602011771号