势能分析法
势能分析法
势能分析通过定义一个势能函数（通常表示为 
\(\Phi\))，度量数据结构的潜在能量，即系统状态中的预留资源，这些资源可以用来支付未来的高成本操作。势能的变化用于平衡操作序列的总成本，从而确保整个算法的均摊成本在合理范围内。
——摘自 OI-wiki
原理
定义状态 \(S\) 为某一时刻数据结构的状态，初始状态为 \(S_0\)。
其次，定义的势能函数 \(\Phi(S)\) 需要满足以下两个性质：
- 初始势能：\(\Phi(S_0)=0\)。
- 非负性：任意状态下 \(\Phi(S)\geq 0\)。
Ps：也有说法表示不必满足以上性质，势能函数反映数据结构变化量即可。
对于每个操作，均摊成本 \(\hat c\) 定义为
其中 \(c\) 为这次操作所需的实际复杂度。
该公式表明均摊成本等于实际成本加势能变化量。
有一种理解方式是：当 \(c\) 小时，势能增加 \(\Phi(S_i)>\Phi(S_{i-1})\)；当 \(c\) 大时，势能减小 \(\Phi(S_i)<\Phi(S_{i-1})\)。
我们通过势能函数来分析一系列操作的总成本。
例题：动态数组的扩容分析
题面
初始时数组大小为 \(0\)，第一次加入数组大小会变为 \(1\)。之后每次加入时，如果数组大小不够，会新开一个大小为原来两倍的数组，在新数组中依次插入原来的数据与当前插入的数。
若不计开新数组的时间，单次插入 \(O(1)\)，分析插入 \(n\) 个数时的复杂度。
分析
设数组长度为 \(m\)，插入的数的个数为 \(n\)，设势能函数 \(\Phi_i=2n-m\)。
-
插入操作（不扩容）
操作成本：\(c=1\)。
势能变化：\(n_i=(n_{i-1}+1),m_i=m_{i-1}\)，\(\Phi_i-\Phi_{i-1}=(2\cdot n_i+m_i)-(2\cdot n_{i-1}+m_{i-1})=2\)。
均摊成本：\(\hat c=c+\Phi_i-\Phi_{i-1}=2\)。
-
插入操作（扩容）
操作成本：\(c=n+1\)。
势能变化：\(n_i=(n_{i-1}+1),m_i=2\cdot m_{i-1}=2\cdot n_{i-1}\)，\(\Phi_i-\Phi_{i-1}=(2\cdot n_i+m_i)-(2\cdot n_{i-1}+m_{i-1})=2-n\)。
均摊成本：\(\hat c=c+\Phi_i-\Phi_{i-1}=3\)。
此处看出虽然扩容操作成本高，但势能变化量减小；反之同理。整体均摊在 \(O(1)\) 级别。
实践：分析 Splay 树的复杂度
\(x\) 表示节点 \(x\)，\(|x|\) 表示 \(x\) 的子树大小。
定义 \(\Phi(S)=\sum_{i\in S} \log |x|\)，证明旋转到根的操作是 \(\log n\)。
\(zig-zig\) 与 \(zag-zag\)。
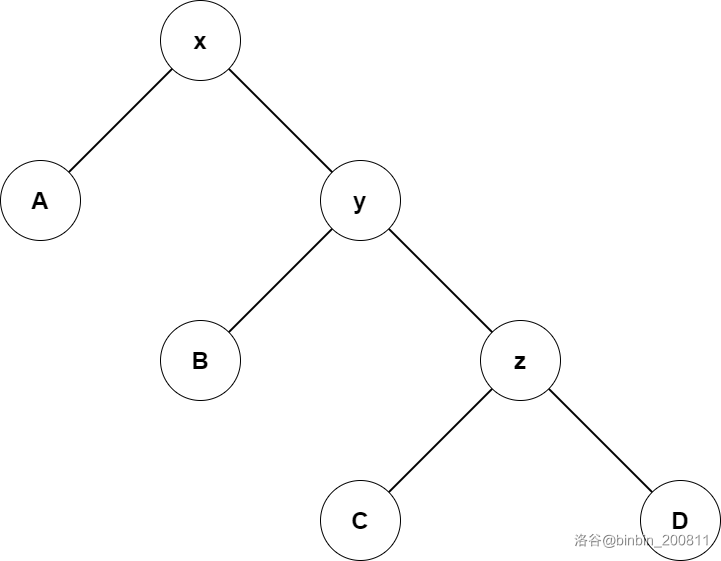
势能变化量为
由于 \(\phi_i(x)=phi_{i-1}(z)\)，所以有
根据子树大小关系推导的 \(\phi\) 关系，可知
观察上面的树，不难发现有
于是我们可以得到（注意与上面的式子不同）
于是均摊势能为
\(zig-zag\) 或 \(zag-zig\)。
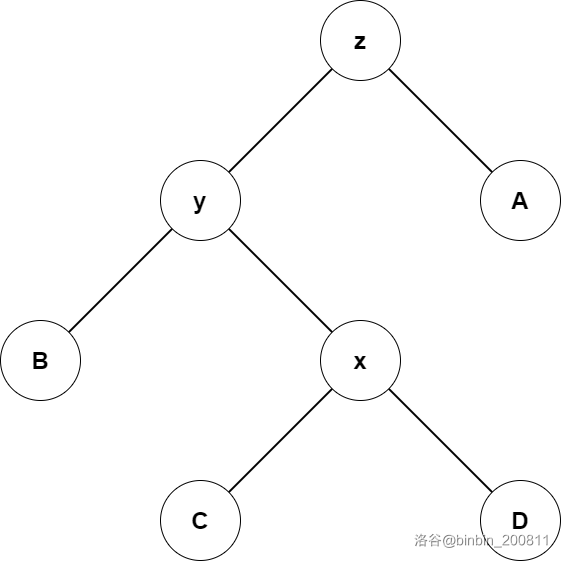
首先还是分析势能变化量
观察上图，可得
同理可得
于是有
\(zig\) 或 \(zag\)
综上，1.2. 两种操作均摊为 \(O(\phi_i(x)-\phi_{i-1}(x))\)，3 的均摊代价是 \(O(1+\phi_i(x)-\phi_{i-1}(x))\)，一次 splay 是若干次 1.2. 操作与一次 3. 操作的结合，所以一次 splay 的代价为 \(O(1+\phi_i(x)-\phi_0(x))\leq O(1+\log n)=O(\log n)\)。
由于其他操作都是基于 splay，在势能函数中以常数的形式体现，于是我们可以估计一棵 Splay 树的平均复杂度是 \(O(\log n)\) 的，现在我们来计算一下
根据上面的分析 \(\sum_{i=1}^n \hat c_i\) 的代价为 \(O(n\log n)\)。
再根据势能函数的定义，有
代入原式
Q.E.D.
习题
栈问题
一个栈，有以下 3 种操作：
- 入栈
- 弹出栈顶元素
- 在栈顶弹出若干元素
通过均摊分析其复杂度。
二进制加法计算器
有一个二进制加法计算器，在 1111+1 时会改变五个数字的值，修改的数字最多达到 \(O(\log n)\)，假设计算器修改一个位置的复杂度是 \(O(1)\) 的，请证明这种计算器执行 +1 是 \(O(1)\) 的。
序列 GCD
给出一个有 \(n\) 个元素的数列，求他们的最大公约数，采用以下算法：
gcd(a,b) = if b==0 return a;
else return gcd(b,a%b)
int main()
ans = a[1]
for(int i=2; i<=n; ++i)
ans = gcd(ans,a[i])
求这个算法的时间复杂度，并给出证明。
习题解析
栈问题
设势能函数 \(\Phi\) 为栈中元素个数，分析操作复杂度。
- \(\hat c=c+\Phi_i-\Phi_{i-1}=1+1=2\)
- \(\hat c=c+\Phi_i-\Phi_{i-1}=1-1=0\)
- \(\hat c=c+\Phi_i-\Phi_{i-1}=k+(\Phi_{i-1}-k)-\Phi_{i-1}=0\)。
仅入栈时均摊复杂度为 \(O(1)\)，时间复杂度为 \(O(n)\)。
二进制加法计算器
设势能函数 \(\Phi\) 为目前计算器中 1 的数目。
-
相加不进位
\(\hat c=c+\Phi_i-\Phi_{i-1}=1+1=2\)
-
相加进位
\(\hat c=c+\Phi_i-\Phi_{i-1}=k+(\Phi_{i-1}-k+1)-\Phi_{i-1}=1\)
均摊复杂度为 \(O(1)\)。
序列 GCD
设势能函数 \(\Phi\) 为当前数的大小，考虑从最终状态转移回初始状态。
-
求完一次后 gcd 不改变
\(\hat c=c+\Phi_i-\Phi_{i-1}=1+0=1\)
-
求完一次后 gcd 改变
\(\hat c=c+\Phi_i-\Phi_{i-1}\leq k+2^k\)
由于势能函数小于 \(a_1\)，\(2^k\) 的和小于 \(a_1\)。
时间复杂度为 \(O(n+\log n)\)。
浙公网安备 33010602011771号