对“树”的一些理解
我们理解一个新的事物,无非是先知道它的定义,再关联一些相似的事物,然后再结合一些实际应用场景。我们就按这个套路理解下“树”这种结构。
讲树之前,我们先回顾下基本的数组和链表。
数组
数组是申请一段连续的内存空间来存储相同类型的数据,由于是相同类型的数据,我们就可以根据数据类型的长度(比如int类型,占用4个字节),对内存地址进行运算,从而定位到某个位置。这种结构不用单独保存位置信息,所以它的空间利用效率是最高的。

但这种结构也导致插入和删除元素时,必然要移动数据来“腾出”空间。例如在2和3之间插入6,则分别要把3、4、5向右移动一位,腾出一个空位,再把6写入。
链表
顾名思义,是通过"链"来连接各个元素,中间必然有专门负责连接的数据,其实就是位置信息,即每个元素除了它自身的数值,还保存了它下个节点的“地址”,构成一个个“节点”。所以它能把内存中不连续的地址空间连接起来,用额外的位置信息链了更多的内存地址。这种结构决定了修改位置信息就能实现对元素的插入和删除。例如删除节点3,只需要把节点2的位置指向节点4即可。在节点1和节点2之间插入一个节点5,则只需把节点1位置指向节点5,同时节点5位置指向节点2即可,而无需移动数据。

树
可以看作是链表的扩展,一个节点对应了多个节点。节点里包含一个或多个元素,当然还有其他节点的位置信息,否则就失去联系了。节点从上到下逐渐扩展(分叉、分枝),类似于树的树杈,树杈又长出其他树杈,最终呈现出一棵倒立过来的树。
现实中的树可以长出多个树杈,对应到数据结构上就是“多叉树”。叉可以理解为分叉,二叉就是对应了两个分叉、两个子节点(左节点和右节点),当然二叉树不是要求每个节点必须有两个子节点,也可以少于两个。
我们再熟悉下树的几个基本概念:
节点,构成树的基本单位,里面有元素、位置信息。节点之间存在关系,如节点7的父节点是10,子节点是6和8,兄弟节点是12。
根节点,没有父节点的节点,如节点5。
叶子节点,没有子节点的节点,如节点1、6、9。
高度,节点到叶子节点的最大边数。如该树的高度为4
接下来我们从最简单的两个分叉的“二叉树”开始,看看它是如何通过附加限制来优化查询的。
限制节点位置
限制左右节点的大小,使一个树中的任意一个节点的左子节点值小于它,右子节点值大于它(回想一下快速排序的基准值,二分法的中间值都是这个道理)。满足这种限制的我们称为“二叉查找树(Binary Search Tree)”,对应的查找过程其实就是二分法。只不过把左右区间换成了左右子树。
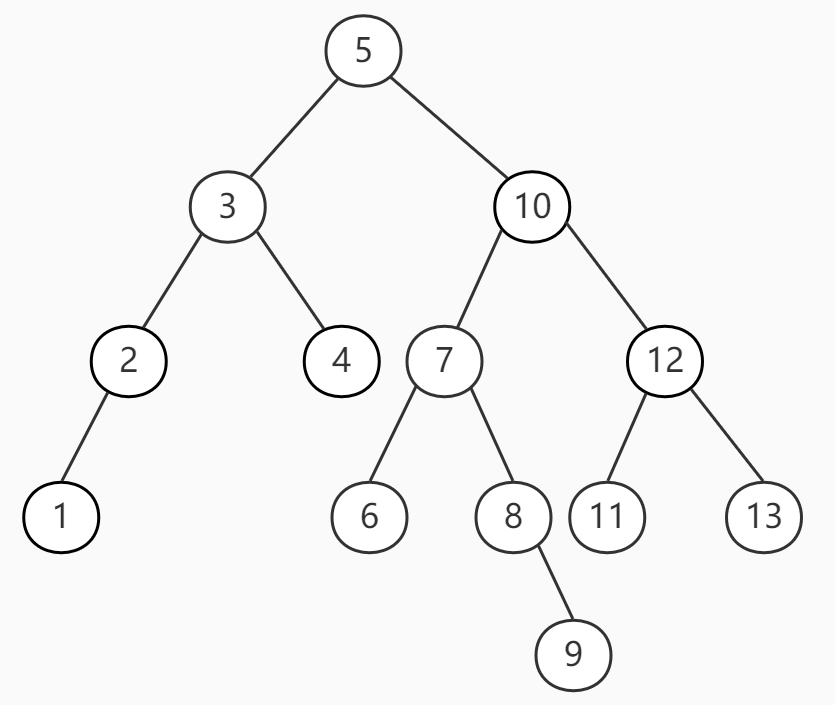
我们再看下节点的插入,由于要保持这种特性,必然对节点的插入位置有所限制。基本规则也是比较大小,找到位置。例如把6插入到这个树时,6>5,所以在右侧子树继续查找,6<10,左侧,6<7,且7的左侧节点为空,所以把7的左节点设置为节点6。
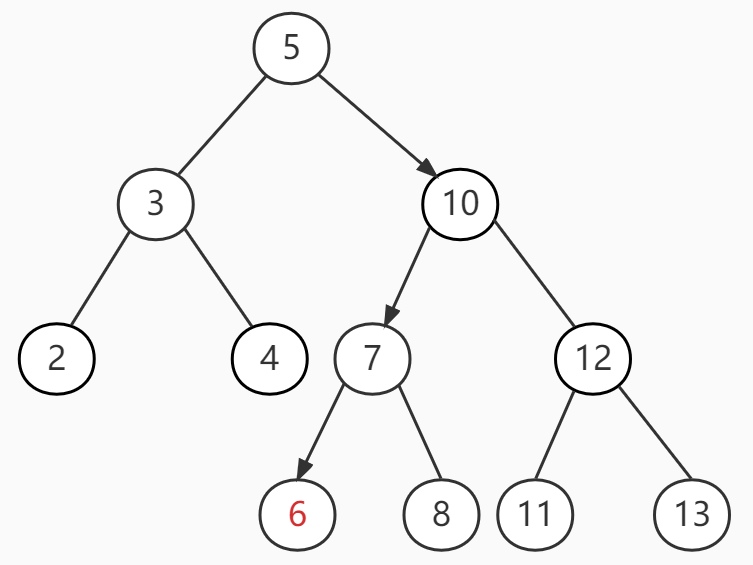
再看下删除
1 删除单一节点(无子节点)直接删除即可,例如节点1
2 删除节点只有一个子节点时,直接把其父节点指向剩余的一个节点即可,例如节点2
3 删除的节点有两个节点时,例如节点10,我们可以取10左侧子树的最大节点9,或者取右侧子树的最小节点11,直接替换即可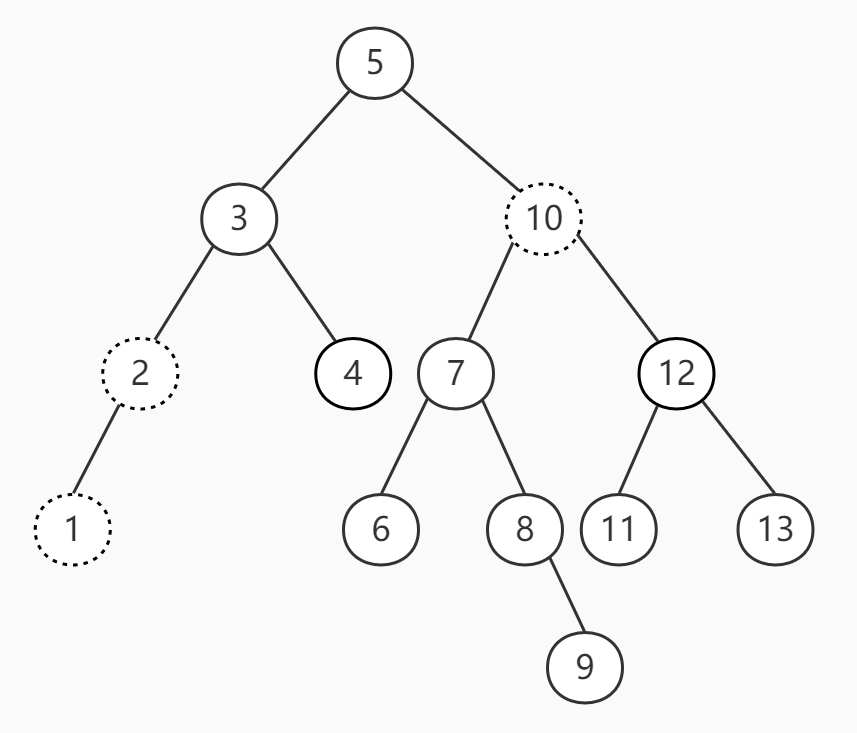
从插入和删除过程我们能看出节点的出现顺序,对树的结构是有影响的,难免出现这种情况:
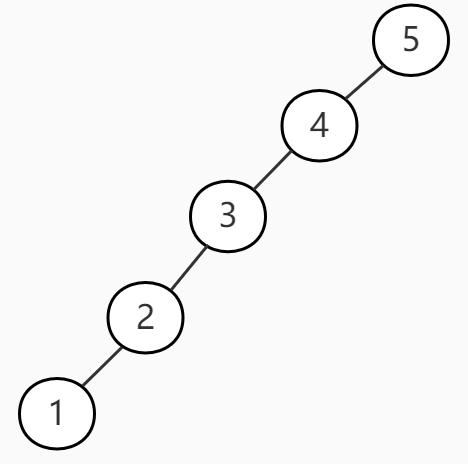
或者
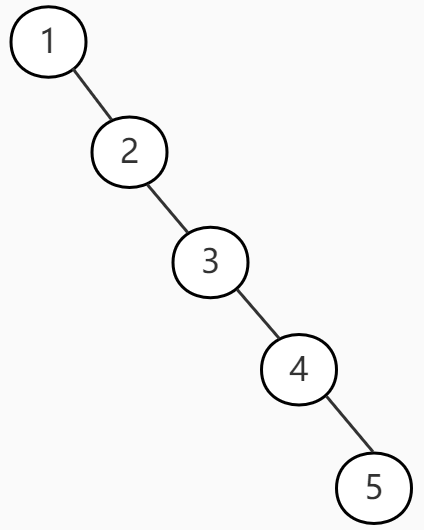
这种形态下的树已经退化为有序的链表结构(树的高度达到最大)。所以我们要继续增加对高度的限制。
限制高度
任意一个节点的左右子树的高度差不大于1。
我们把同时满足这种限制的树称为“平衡二叉树(Balanced Binary Search Tree)”,准确说应该是实现了自身平衡的二叉查找树。其实就是为了降低整个树的高度,避免出现二叉查找树中退化成链表的问题。处理的核心就是怎么调整节点的位置达到平衡状态,具体平衡算法及可视化处理流程可以参考这两种实现。
1 AVL树(Adelson-Velskii-Landis Tree),一种严格平衡的树
https://zhuanlan.zhihu.com/p/34899732
https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
2 红黑树(Red-Black Tree),引入节点颜色的概念,放松了高度的限制,从而降低维持平衡的成本
https://zhuanlan.zhihu.com/p/80647496
https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
最后我们看下B树,它又增加了什么限制呢?
B树(B-Tree,注意这里的-是折线符,不是B减树,B代表Balance平衡的意思,所以它也属于一种平衡树)。当我们在一个节点只存放一个元素且分叉只有两个时,必然会导致树的高度过高(虽然通过平衡降低了一些高度)。那么我们就加大节点里的元素和分叉的数量,来更有效地降低高度。所以我们把B树看作是限制了节点的最少元素和分叉的一种平衡树。
这里我们引入“阶”(order)的概念,就是节点对应的子节点的“个数”, 只不过这里的“个数”要取最大值。例如一个节点里有两个元素[11 15],则这个节点最多能对应三个子节点,分别是11左边对应一个,11和15中间对应一个,15右侧一个,所以它就是一个三阶的B树。类似一根绳子剪一刀就是2节(阶),剪两刀就是三节(阶)。
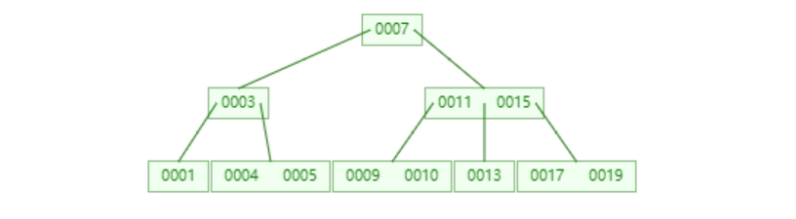
图片生成来源于https://www.cs.usfca.edu/~galles/visualization/BTree.html
所以阶数越高对应节点中元素就越多,分叉也就越多,整个树的高度降低效果就越明显。例如一个101阶(元素最多100个)的一个高度为2的B树,可以存储100万个元素。1001阶则可以存储10亿个元素。
具体可视化的平衡过程见这里 https://www.cs.usfca.edu/~galles/visualization/BTree.html
B+树
可以看作是B树的一个加强版。它在叶子节点存储了所有的元素,并且每个叶子节点保存了到下个叶子节点的位置,构成了一个有序的链表。B树结构下做范围查询(类似数据库的范围查询)时,可能会多次读取中间节点(父节点)来确定左或右叶子节点,而B+树叶子节点的有序链表能跳过对中间节点的读取,一直遍历到对应的范围最大值。如图示

另外,B+树非叶子节点是不存储数据的,所以它就能保存更多的索引(位置)数据。
可视化的平衡过程见这里 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
总结
可以看出不同形态的树的演变过程,就是对节点位置、数量及节点内部数据附加各种规则的过程,从而实现了对数据的高效操作。
扩展阅读
B树
https://www.jianshu.com/p/a858bb15cbf0
https://www.yiibai.com/data_structure/b-tree.html
https://www.bilibili.com/video/BV1e5411T77z
其他算法的演示(包括之前介绍的各种排序算法)
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

 浙公网安备 33010602011771号
浙公网安备 33010602011771号