【题解】CF1583E Moment of Bloom

题面传送门

解决思路

没有思路时可以先手玩样例。

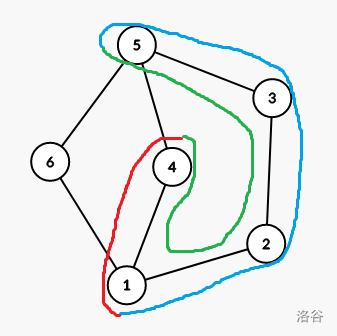
以样例 \(1\) 为例，我们把每条路径的顺序重排一下，得到了以下结果：\(4\to 1,1\to 5,5\to 4\) 。可以发现，构成了一个环。一个路径环可以使其中每条路径走过 \(2\) 次，同时也意味着环上的每个点作为起点或终点出现了 \(2\) 次。能否推广到偶数次呢？假设我们给样例 \(1\) 加上 \(3\) 条路径：\(1\to 6,6\to 4,4\to1\)，这时 \(1,4\) 分别都出现了 \(4\) 次。我们只需要再添一个经过 \(1,4,5,6\) 的环即可，仍然满足要求。

所以，得出结论：若所有起点终点都出现了偶数次，即满足了题目要求。

然后考虑如何求出路径。因为要求出现次数为 \(2\) 的一组点连成的路径构成一个环，所以任意两点之间走的要是同一条路径，树就满足这一条件。所以考虑建出原图的任意生成树，然后跑 \(\text{dfs}\) 即可找出路径。具体可以看代码。

那不满足要求怎么办？以样例 \(2\) 为例，\(1,2,3,5\) 三个点作为起点或终点出现了奇数次。所以，只要在它们之间每两个加一条路径即可，需要添加的路径条数 \(=\) 作为起点或终点出现奇数次的点数 \(\div 2\)。

AC Code

#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
#define TIE cin.tie(0),cout.tie(0)
#define int long long
using namespace std;
int n,m,u,v,q,d[300005],s[300005],t[300005],ans;
vector<int> a[300005],b;
bool fl;
struct DSU{
	int fa[300005];
	void init(int n){
		for(int i=1;i<=n;i++) fa[i]=i;
	}
	int find(int x){
		if(x==fa[x]) return x;
		return fa[x]=find(fa[x]);
	}
	void merge(int x,int y){
		fa[find(x)]=find(y);
	}
	bool query(int x,int y){
		return find(x)==find(y);
	}
}dsu;
void dfs(int x,int fa,int to){
	for(int i=0;i<a[x].size();i++){
		int tmp=a[x][i];  
		if(tmp==fa) continue;
		b.push_back(tmp);  
		if(tmp==to){   //走到了
			fl=1;
			return ;
		}
		dfs(tmp,x,to);
		if(fl) return ;
		b.pop_back();
	}
}
signed main(){
	IOS;TIE;
	cin>>n>>m;
	dsu.init(n);
	for(int i=1;i<=m;i++){
    		cin>>u>>v;
		if(!dsu.query(u,v)){
			dsu.merge(u,v);
			a[u].push_back(v);
			a[v].push_back(u);  //建成一颗树
		}
	}
	cin>>q;
	for(int i=1;i<=q;i++){
		cin>>s[i]>>t[i];
		d[s[i]]++,d[t[i]]++;  //作为起点或终点出现次数
	}
	for(int i=1;i<=n;i++) if(d[i]&1) ans++;
	if(ans==0){
		cout<<"YES"<<endl;
		for(int i=1;i<=q;i++){
			b.clear(),fl=0,b.push_back(s[i]);  //b记录路径
			dfs(s[i],0,t[i]);
			cout<<b.size()<<endl;
			for(int j=0;j<b.size();j++) cout<<b[j]<<' ';
			cout<<endl;
		}
	}
	else cout<<"NO"<<endl<<ans/2<<endl;  
	return 0;
}