【题解】CF919D Substring

题面传送门

解决思路：

DP 与拓扑结合。$f_{i,j}$ 表示到 $i$ 位置 $j$ 的最大次数。

将 $a\sim z$ 转成数字 $0\sim 25$ ，方便存储。

考虑转移。这一部分其他题解讲的很详细了，也很好理解。对于二十六个字母（$j$）：

• 若是当前节点，则 $f_{tmp,j}=max(f_{tmp,j},f_{k,j}+1)$

• 否则 $f_{tmp,j}=max(f_{tmp,j},f_{k,j})$

其中 $tmp$ 为当前搜到的节点，$k$ 为其父节点。

然后考虑如何判环。例如以下情况：

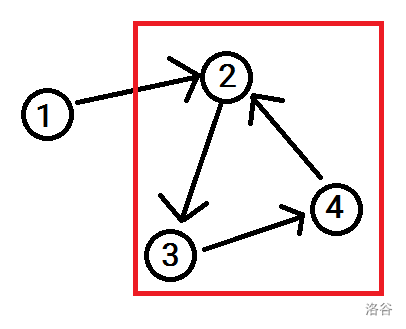
红框中显然是环。

模拟其处理过程。第一次删掉了入度为 $0$ 的 $1$ 号节点：

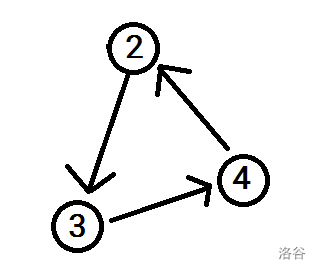
然后会发现，这时没有入度为 $0$ 的节点可以找了，队列为空，结束 BFS。

而对于没有环的情况，所有点都是会被遍历到的。

所以，用 $cnt$ 记录遍历过点的数量，若最后 $cnt<n$，则说明有环。

细节讲好了，程序中就不再注释了。

Code：

#include<bits/stdc++.h>
using namespace std;
int n,m,b[300005],in[300005],f[300005][26];
int ans,cnt,x,y;
string s;
vector<int> a[300005];
queue<int> q;
int main(){
	scanf("%d%d",&n,&m);
	cin>>s;
	for(int i=1;i<=n;i++) b[i]=s[i-1]-'a',f[i][b[i]]++;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		in[y]++;
		a[x].push_back(y);
	}
	for(int i=1;i<=n;i++) if(!in[i]) q.push(i);
	while(q.size()){
		int k=q.front();
		q.pop();
		cnt++;
		for(int i=0;i<a[k].size();i++){
			int tmp=a[k][i];
			for(int j=0;j<26;j++){
				if(b[tmp]==j) f[tmp][j]=max(f[tmp][j],f[k][j]+1);
				else f[tmp][j]=max(f[tmp][j],f[k][j]);
			}
			in[tmp]--;
			if(!in[tmp]) q.push(tmp);
		}
	}
	if(cnt<n) printf("-1");
	else{
		for(int i=1;i<=n;i++){
			for(int j=0;j<26;j++) ans=max(ans,f[i][j]);
		}
		printf("%d",ans);
	}
	return 0;
}