AI量化策略,我该如何理解你?
人工智能(AI)技术得到了飞速发展,其在各个领域的运用也不断取得成果。机器学习被评为人工智能中最能体现人类智慧的技术,因此开发AI量化策略可以理解为将机器学习应用在量化投资领域。
理解机器学习算法——以StockRanker为例
机器学习算法太多,本文讨论只针对适用于金融数据预测的常用有监督型机器学习(Supervised Machine Learning)算法:StockRanker。假设我们要去预测某个连续变量$ Y 未 来 的 取 值 , 并 找 到 了 影 响 变 量 未来的取值,并找到了影响变量 未来的取值,并找到了影响变量 Y 取 值 的 取值的 取值的K$ 个变量,这些变量也称为特征变量(Feature Variable)。机器学习 即是要找到一个拟合函数 f ( X 1 , X 2 , … , X K ∣ Θ ) f(X_1,X_2,\ldots,X_K|\Theta) f(X1,X2,…,XK∣Θ)去描述 Y Y Y和特征变量之间的关系, Θ \Theta Θ为这个函数的参数。
要找到这样的函数,必须要足够量的观测数据,假设有 N 个样本数据$ { y_1,y_2,\ldots,y_n }$和
x
1
i
,
x
2
i
,
…
,
x
K
i
x_{1i},x_{2i},\ldots,x_{Ki}
x1i,x2i,…,xKi(其中
i
=
1
,
2
,
…
,
n
i=1,2,\ldots,n
i=1,2,…,n)。然后定义一个函数
L
L
L来衡量真实观测数据和模型估计数据偏差,函数 L 也称作损失函数(Loss Function)。基于历史观测数据,我们可以求解下列的最化问题来得到参数
Θ
\Theta
Θ 的估计值 。
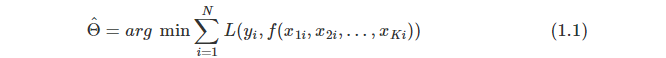
求解(1.1)过程称作模型训练(Model Traing)。基于特征变量的最新观测值和训练出来的模型参数就可以预测
y
y
y的数值。 接下来,我们以一个具体的AI量化策略看一下用机器学习方法开发策略的具体流程。
开发AI量化策略的流程
使用机器学习开发策略的流程如下图所示:
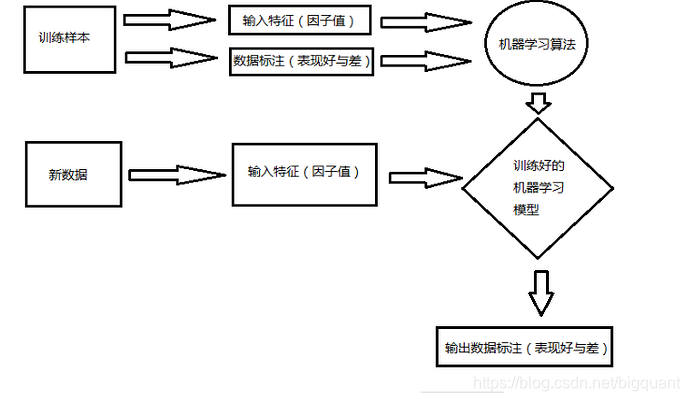
为便于理解,以StockRanker为例介绍。StockRanker是一种监督式股票排序学习算法,假设我们要预测个股未来
n
n
n天的收益率,然后将其进行排序, 使用该算法在新的一天数据上进行预测,可以向我们推荐应该买入哪些股票。我们结合上图介绍下使用StockRanker算法来开发量化策略的流程。
- 首先,确定目标。因为是监督学习,因此需要对收益率数据进行标注。
- 接着,数据划分。将所有数据划分为训练数据和测试数据,训练数据用来训练模型,测试数据用来检验模型的表现。
- 然后,特征构造。特征构造是至关重要的一步,特征构造的好将会直接影响模型效果和策略表现。在这一步,你在金融行业的专业知识和投资经验将发挥很大的作用。
- 然后,训练和预测。在特征构造完毕后,就可以训练好StockRanker算法并进行预测。
- 最后,策略回测。根据StockRanker预测结果进行策略回测,获取策略表现。
关于AI策略的预测能力
量化交易人员对机器学习的态度很复杂,一方面自己实际投资中发现选股因子和股票收益之间关系并非完全线性,需要能力更强的分析预测工具,另一方面又担心机器学习工具过于复杂,导致数据挖掘,样本内过拟合的结果外推性不强,经济含义也不好解释。我们这里想说明的是,ML(Machine learning)虽然没法完全避免过拟合的可能性,但配合使用一些方法是可以降ML低过拟合的概率,提升样本外预测能力的。
假设输入变量$ X$ 和输出变量 Y Y Y 的真实关系可以表示为 Y = f ( X ) + ϵ Y=f(X)+\epsilon Y=f(X)+ϵ, ϵ \epsilon ϵ为误差项,满足
E ( ϵ ) = 0 E(\epsilon)=0 E(ϵ)=0,KaTeX parse error: Expected 'EOF', got '}' at position 32: …\sigma_\epsilon}̲^2 。投资者者通过 ML 方法找到了 f ( X ) f(X) f(X) 的一个拟合函数 f ( x ) ^ \hat{f(x)} f(x)^ 。对于一个新的数据点 X = x 0 X=x_0 X=x0 , 它的预测偏差定义为:
E
r
r
(
X
0
)
=
E
[
(
Y
−
f
(
X
0
^
)
)
2
∣
X
=
x
0
]
Err(X_0)=E[(Y-\hat{f(X_0}))^2|X=x_0]
Err(X0)=E[(Y−f(X0^))2∣X=x0]
=
σ
ϵ
2
+
[
E
f
(
x
0
^
)
−
f
(
x
0
)
]
2
+
E
[
f
(
x
0
)
^
−
E
f
(
x
0
)
^
]
2
={\sigma_\epsilon}^2+[E \hat{f(x_0}) -f(x_0)]^2 + E[\hat{f(x_0)}-E\hat{f(x_0)}]^2
=σϵ2+[Ef(x0^)−f(x0)]2+E[f(x0)^−Ef(x0)^]2
=
σ
ϵ
2
+
B
i
a
s
2
f
(
x
0
)
^
+
V
a
r
(
f
(
x
0
)
^
)
(
1.2
)
={\sigma_\epsilon}^2+ Bias^2\hat{f(x_0)} + Var(\hat{f(x_0)}) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1.2)
=σϵ2+Bias2f(x0)^+Var(f(x0)^) (1.2)
ML模型的预测偏差取决于(1.2)的这三项,第一项取值与 ML 模型选择无关,第二项
B
i
a
s
Bias
Bias 和第三项
V
a
r
i
a
n
c
e
Variance
Variance 的理解可以参考下图,两者都受 ML 模型复杂度的影响;
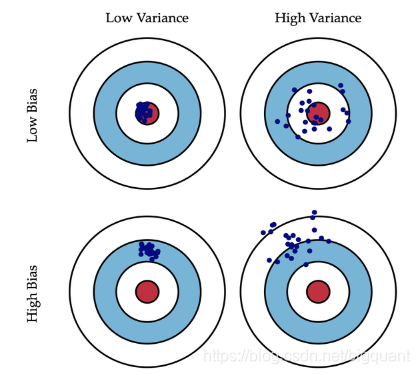
一般来讲,模型复杂度越高,
B
i
a
s
Bias
Bias 越小,但
V
a
r
i
a
n
c
e
Variance
Variance 越大;模型复杂度越低,
B
i
a
s
Bias
Bias越大,
V
a
r
i
a
n
c
e
Variance
Variance越小。从下图可以看出,当模型复杂度较高的时候,虽然偏差很小,但是模型方差很大,因此模型的泛化能力不高。
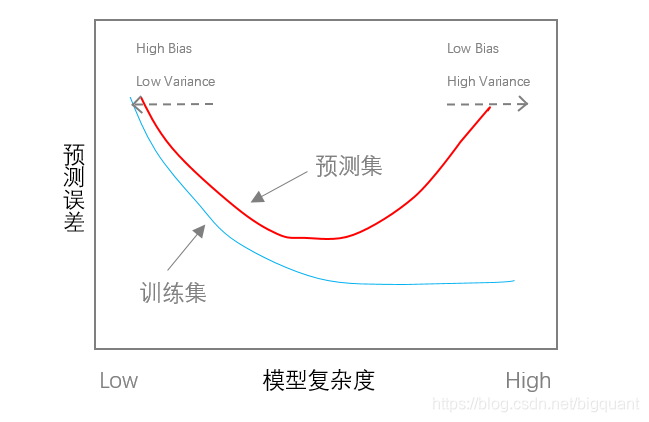
因此要想提高 ML模型的预测能力,模型并不是越复杂越好,而是要在
B
i
a
s
Bias
Bias 和
V
a
r
i
a
n
c
e
Variance
Variance 间做权衡,降低总体预测误差,也就是所谓的
B
i
a
s
−
V
a
r
i
a
n
c
e
t
r
a
d
e
−
o
f
f
Bias -Variance \ \ trade-off
Bias−Variance trade−off。
对待机器学习,我们应该摆脱固有的“黑箱“和”过拟合“概念,一些 ML 算法的逻辑非常直白,而且 ML 在求解优化问题估计模型参数时,通常会带正则化约束条件,通过交叉验证的方式来选择参数,避免过拟合。 众多的实践研究说明, ML 方法的预测能力大部分情况下都强于线性模型。
总结
AI量化策略在收益和稳健性上都要比传统的线性模型高,更重要的是它可以帮助我们省去Barra结构风险模型中”因子筛选“、”因子加权“和”组合优化“的过程,提升策略开发效率。感兴趣的朋友可以前往BigQuant平台进行体验~
原文链接:《AI量化策略,我该如何理解你?》


 浙公网安备 33010602011771号
浙公网安备 33010602011771号