335. Self Crossing

You are given an array x of n positive numbers. You start at point (0,0) and moves x[0] metres to the north, then x[1] metres to the west, x[2] metres to the south, x[3] metres to the east and so on. In other words, after each move your direction changes counter-clockwise.

Write a one-pass algorithm with O(1) extra space to determine, if your path crosses itself, or not.

Example 1:

Given x = [2, 1, 1, 2],
Return true (self crossing)

Example 2:

Given x = [1, 2, 3, 4],
Return false (not self crossing)

Example 3:

Given x = [1, 1, 1, 1],
Return true (self crossing)

给定一个含有n个正整数的数组x[n]，从第1个元素开始，向北移动x[0]，接着向西移动x[1]，接着向南移动x[2]，再向东移动x[3]……如此按逆时针循环，直至最后一个数。写一个空间复杂度为O(1)的算法，判断该移动过程中轨迹是否有相交。

本人未找到解决方法，越想越复杂，惭愧！下面是参考的这位网友，感谢分享！

分析：

相交的情况有以下3种：

第一类是第四条边和第一条边相交的情况，需要满足的条件是第一条边大于等于第三条边，第四条边大于等于第二条边。同样适用于第五条边和第二条边相交，第六条边和第三条边相交等等，依次向后类推的情况。

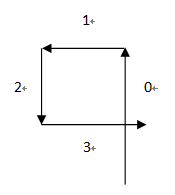
第二类是第五条边和第一条边重合相交的情况，需要满足的条件是第二条边和第四条边相等，第五条边大于等于第三条边和第一条边的差值，同样适用于第六条边和第二条边重合相交的情况等等依次向后类推。

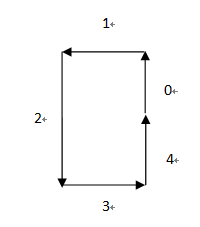
第三类是第六条边和第一条边相交的情况，需要满足的条件是第四条边大于等于第二条边，第三条边大于等于第五条边，第五条边大于等于第三条边和第一条边的差值，第六条边大于等于第四条边和第二条边的差值，同样适用于第七条边和第二条边相交的情况等等依次向后类推。

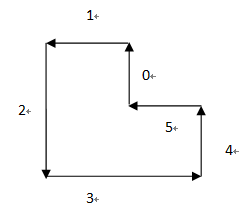
由此，代码如下：

bool isSelfCrossing(vector<int>& x)
{
	for (int i = 3; i < (int)x.size(); i++)
	{
		if (x[i] >= x[i - 2] && x[i - 1] <= x[i - 3])
			return true;
		if (i >= 4 && x[i - 1] == x[i - 3] && x[i] >= x[i - 2] - x[i - 4])
			return true;
		if (i >= 5 && x[i - 2] >= x[i - 4] && x[i - 3] >= x[i - 1] && x[i - 1] >= x[i - 3] - x[i - 5] && x[i] >= x[i - 2] - x[i - 4])
			return true;
	}
	return false;
}