笔记
康托展开和逆康托展开
康托展开和逆康托展开(转) - Sky丨Star - 博客园 (cnblogs.com)
康托展开表示的就是是当前排列组合在n个不同元素的全排列中的名次
逆康托展开则是由名次得出该名次的排列组合
公式:康托展开值X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!
X表示该排列组合前面有X个排列组合,所以该排列组合是第X+1个
a[i]表示当前未用到的元素中该元素排第几个
//阶乘 static const int Fac[]={1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; //康托展开 int cantor(int *a,int n){ int x=0; for(int i=0;i<n;++i){ int cnt=0; for(int j=i+1;j<n;++j) if(a[j]<a[i])cnt++; x+=Fac[n-i-1]*cnt; } return x; } //逆康托展开 void decantor(int x,int n){//x为康托展开值,n为元素个数 vector<int>v;//存放当前可选数 vector<int>a;//所求排列组合 for(int i=1;i<=n;++i)v.push_back(i); for(int i=n;i>=1;--i){ int l=x%Fac[i-1]; int r=x/Fac[i-1]; x=l; a.push_back(v[r]); v.erase(v.begin()+r); } }
__int128的使用方法
__int128 就是占用128字节的整数存储类型,范围是 -2^127~2^127-1
_int128只能实现四则运算,不能用cin,cout,scanf,printf输入输出,用快读和快写的函数
#define int __int128
inline void read(int &n){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
n=x*f;
}
inline void print(int n){
if(n<0){
putchar('-');
n*=-1;
}
if(n>9) print(n/10);
putchar(n % 10 + '0');
}
Lucas
int ksm(int x,int y){ int res=1; while(y){ if(y&1)res=res*x%mod; x=x*x%mod; y>>=1; } return res; } int c(int a,int b){ if(b>a)return 0; int res=1; for(int i=1,j=a;i<=b;++i,--j){ res=res*j%mod; res=res*ksm(i,mod-2)%mod; } return res; } int Lucas(int a,int b){ if(a<mod&&b<mod)return c(a,b); return c(a%mod,b%mod)*Lucas(a/mod,b/mod)%mod; }
阶乘逆元求组合数
int fact[N], infact[N];
int ksm(int a, int k, int p) {
int res = 1;
while (k) {
if (k & 1)res = res * a % p;
k >>= 1;
a = a * a % p;
}
return res;
}
void init() {
fact[0] = infact[0] = 1;
for (int i = 1; i < N; ++i) {
fact[i] = fact[i - 1] * i % mod;
infact[i] = infact[i - 1] * ksm(i, mod - 2, mod) % mod;
}
//C(a,b)=fact[a]*infact[a-b]%mod*infact[b]%mod;
}
int C(int a, int b) {
if (a < b || a < 0 || b < 0) return 0ll;
return fact[a] * infact[b] % mod * infact[a - b] % mod;
}
struct E{ int x,y; E(){} E(int _x,int _y){x=_x,y=_y;} E operator-(E b){return E(x-b.x,y-b.y);} double len(){return ::hypot(x,y);}//sqrt(x*x+y*y); };
博弈论
Nim游戏
- 有n堆石子,两人轮流取石子,取不到的败
结论:每堆石子数异或和为非0则先手胜,否则先手败
- 有n个台阶,每个台阶有若干石子,两人轮流扔石子,石子被扔到下一台阶(到地面为止),无法扔的败
结论:所有第奇数个台阶的异或和为非0则先手胜,否则先手败
- 有n堆石子和一个集合S,两人轮流取石子,只能取si个石子,取不到的败
结论:所有堆数的SG异或和为非0则先手胜,否则先手败
//f初始为-1,sg(0)=0 vector<int>s,f(N); int sg(int x){ if(f[x]!=-1)return f[x]; unordered_set<int>se; for(int i=0;i<k;++i){ if(s[i]<=x)se.insert(sg(x-s[i])); } for(int i=0;;++i)if(!se.count(i))return f[x]=i; }
有n堆石子,两人轮流取一堆石子,换取两堆石子数都不超过被取堆的石子数的石子,不能取的败
结论:所有堆数的SG异或和为非0则先手胜利,否则先手败
//f初始为-1 vector<int>f(105); int sg(int x){ if(f[x]!=-1)return f[x]; unordered_set<int>se; for(int i=0;i<x;++i){ for(int j=0;j<=i;++j) se.insert(sg(i)^sg(j)); } for(int i=0;;++i)if(!se.count(i))return f[x]=i; }
anti_nim游戏
- 当每堆石子的个数都为一时,异或和为零,则先手必胜;
- 当有至少一堆石子的个数>1时,异或和不为零,则先手必胜;
欧拉函数
int cnt,primes[N],phi[N]; bool st[N]; int n; void get_phi(int n){ phi[1]=1; for(int i=2;i<=n;++i){ if(!st[i])phi[i]=i-1,primes[cnt++]=i; for(int j=0;primes[j]*i<=n;++j){ int t=i*primes[j]; st[t]=true; if(i%primes[j]==0){ phi[t]=phi[i]*primes[j]; break; } else phi[t]=phi[i]*(primes[j]-1); } } }
欧拉反演

线性基
详细→线性基详解-CSDN博客

构造线性基
//插入x void add(ll x) { for(int i=60;i>=0;i--) { if(x&(1ll<<i))//注意,如果i大于31,前面的1的后面一定要加ll { if(d[i])x^=d[i]; else { d[i]=x; break;//插入成功就退出 } } } }
如何求在一个序列中,取若干个数,使得它们的异或和最大
ll ans() { ll anss=0; for(int i=60;i>=0;i--)//记得从线性基的最高位开始 if((anss^d[i])>anss)anss^=d[i]; return anss; }
用线性基内的元素能异或出的最小值

从一个序列中取任意个元素进行异或,求能异或出的所有数字中第k小的那个
void work()//处理线性基 { for(int i=1;i<=60;i++) for(int j=1;j<=i;j++) if(d[i]&(1ll<<(j-1)))d[i]^=d[j-1]; } ll k_th(ll k) { if(k==1&&tot<n)return 0;//特判一下,假如k=1,并且原来的序列可以异或出0,
就要返回0,tot表示线性基中的元素个数,n表示序列长度 if(tot<n)k--;//类似上面,去掉0的情况,因为线性基中只能异或出不为0的解 work(); ll ans=0; for(int i=0;i<=60;i++) if(d[i]!=0) { if(k%2==1)ans^=d[i]; k/=2; } }
合并线性基
auto merge = [&](auto &d1, auto &d2) {
for (int i = 0; i <= 60; ++i) {
if (d2[i]) add(d1, d2[i]);//往d1线性基插入d2[i]
}
};
带删除线性基
需要离线。首先需要知道每个时间点都干了些什么,如果是加了个数就需要预处理出这个数会在哪里被删掉。处理好这个之后,我们仍然按照时间处理操作,但是需要给插入线性基的数一个时间戳表示这个数被删除的时间,查询的时候只查询时间戳在当前时间之后的。对于线性基的每一位,时间戳应优先保留靠后的一个。
struct {
int p[32], t[32];
void ins(int x, int tim) {
for (int i = 30; ~i; i--) {
if (!(x >> i)) continue;
if (tim > t[i]) swap(x, p[i]), swap(tim, t[i]);
x ^= p[i];
}
}
//取时间戳 >= tim的
int ask(int tim) {
int res = 0;
for (int i = 30; ~i; i--) if (t[i] >= tim) res = max(res, res ^ p[i]);
return res;
}
} LB;
例题
无向连通图中,求1到n任意走的最大边权异或和
解法:将所有环的贡献放入线性基,答案为任意一条链与任意个环的最大异或和
查看代码
// 查询与x异或的最大值
int query_max(int x) {
int ans = x;
for (int i = 60; i >= 0; i--)//记得从线性基的最高位开始
if ((ans ^ p[i]) > ans)ans ^= p[i];
return ans;
}
//将所有环放入线性基
auto dfs = [&](auto dfs, int u, int num) -> void {
val[u] = num, st[u] = 1;
for (auto [v, w]: ve[u]) {
if (st[v]) LB.add(num ^ w ^ val[v]);
else dfs(dfs, v, num ^ w);
}
};
8种球盒问题
https://zhuanlan.zhihu.com/p/429815465?utm_id=0
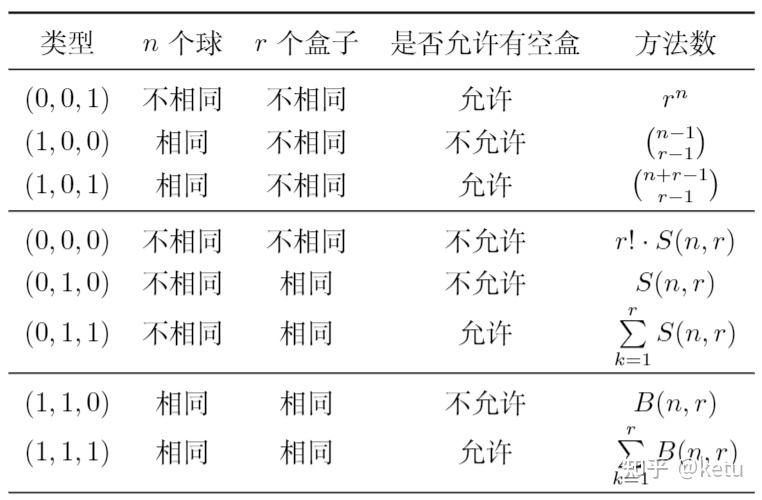
(0,1,0)
int fact[N],infact[N];
int ksm(int a,int k,int p){
int res=1;
while(k){
if(k&1)res=res*a%p;
k>>=1;
a=a*a%p;
}
return res;
}
void init(){
fact[0] = infact[0] = 1;
for (int i = 1 ; i < N; ++i) {
fact[i] = fact[i - 1] * i % mod;
infact[i] = infact[i - 1] * ksm(i, mod - 2, mod) % mod;
}
//C(a,b)=fact[a]*infact[a-b]%mod*infact[b]%mod;
}
int C(int a,int b){
return fact[a]*infact[a-b]%mod*infact[b]%mod;
}
void solve() {
int n,m;
cin>>n>>m;
if(m>n){
cout<<0;
return ;
}
init();
int ans=0;
for(int i=0;i<=m;++i){
if(i%2){
ans=(ans-C(m,i)*ksm(m-i,n,mod)%mod+mod)%mod;
}else{
ans=(ans+C(m,i)*ksm(m-i,n,mod)%mod)%mod;
}
}
cout<<ans*infact[m]%mod;
}
扩展欧几里得
ax+by=c的求解
基本算法:对于不完全为 0 的非负整数 a,b,gcd(a,b)表示 a,b 的最大公约数,必然存在整数对 x,y ,使得 gcd(a,b)=ax+by。
如果a是负数,可以把问题转化成:
|a|(-x) + by = gcd(|a|, x) (|a|为a的绝对值),然后令x' = (-x)。
int exgcd(int a, int b, int &x, int &y) {
if(!b) {
x = 1, y = 0;
return a;
}
int ans = exgcd(b, a%b, y, x);
y -= a / b * x;
return ans;
}
//a,b为不完全为0的非负整数
//ax+by=c
int cal(int a, int b, int c) {///最小正整数解
int x, y, z;
z = exgcd(a, b, x, y);
if(c%z)
return -1;//不成立
// return x;//不需要最小正整数的话直接返回x
// x = -x;//如果a初始为负数,转换为x=-x
x *= c / z;
b = abs(b / z);
return (x%b + b) % b;
}

匈牙利二分图最大匹配
vector<int> st(n + 1), to(n + 1);
auto dfs = [&](int u, auto dfs)->bool {
for (auto v:ve[u]) {
if (st[v]) continue;
st[v] = 1;
if (!to[v] || dfs(to[v], dfs)) {
to[v] = u;
return true;
}
}
return false;
};
for (int i = 1; i <= n; ++i) {
std::fill(st.begin(), st.end(), 0);
if (dfs(i, dfs)) ans ++;
}tarjan求割边割点
无向图求割边
int dfn[N], low[N], ct;
vector<vector<int> > ve;
void tarjan(int u)
{
low[u] = dfn[u] = ++ct;
for (auto v : ve[u])
{
if (!dfn[v])
{
fa[v] = u;
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
add_ge_bian(u, v);
//求割边
}
}
else if (v != fa[u])
low[u] = min(low[u], dfn[v]);
}
}
void work() {
//为连通图
tarjan(1);
}无向图求割点
int dfn[N], low[N], ct;
vector<vector<int> > ve;
void tarjan(int u, bool isroot)
{
int tot = 0;
low[u] = dfn[u] = ++ct;
for (auto v : ve[u])
{
if (!dfn[v])
{
tarjan(v, 0);
low[u] = min(low[u], low[v]);
tot += low[v] >= dfn[u];
}
else
low[u] = min(low[u], dfn[v]);
}
if ((isroot && tot >= 2) || (!isroot && tot >= 1)) {
//割点
add_ge_dian(u);
}
}
void work() {
//为连通图
tarjan(1, 1);
}
tarjan缩点
有向图求强连通分量
int n, m;
cin >> n >> m;
vector<vector<int> > ve(n + 1);
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
ve[u].push_back(v);
}
vector<int> dfn(n + 5), low(n + 5), vis(n + 5), bel(n + 5), sz(n + 5);
// bel表示每个点属于的强连通分量,bel[u] = bel[v]表示u和v在一个强连通分量中
int bccnt = 0, idx = 0;
// bccnt表示强连通分量的个数, sz[i]表示i这个强连通分量的大小
stack<int> st;
auto dfs = [&](int u, auto dfs) -> void {
dfn[u] = low[u] = ++idx;
st.push(u);
vis[u] = 1;
for (auto v: ve[u]) {
if (!dfn[v]) {
dfs(v, dfs);
low[u] = min(low[u], low[v]);
} else {
if (vis[v]) low[u] = min(low[u], dfn[v]);
}
}
if (dfn[u] == low[u]) {
int p;
++ bccnt;
do {
p = st.top();
st.pop();
bel[p] = bccnt;
vis[p] = 0;
sz[bel[p]]++;
} while (p != u);
}
};
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
dfs(i, dfs);
}
}
//缩点+建图
for (int i = 1; i <= n; ++i) {
for (auto v: ve[i]) {
if (bel[i] != bel[v]) {
// add_edge(bel[i], bel[v])
}
}
}边双连通分量
定义:不存在割边的极大双连通子图
性质:边双连通分量中任意一条边都包含在至少一个简单环中
vector<int> dfn(n + 5), low(n + 5), bel(n + 5);
// bel表示每个点属于的边双连通分量,bel[u] = bel[v]表示u和v在一个边双中
int bccnt = 0, idx = 0;
stack<int> st;
auto dfs = [&](int u, int fa, auto dfs) -> void {
dfn[u] = low[u] = ++idx;
st.push(u);
for (auto v: ve[u]) {
// 注意:若存在重边,需要记录每条边的编号
// 判是否遍历的上一条边,而不是判fa
if (v == fa) continue;
if (!dfn[v]) {
dfs(v, u, dfs);
low[u] = min(low[u], low[v]);
} else low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
int p;
++ bccnt;
do {
p = st.top();
st.pop();
bel[p] = bccnt;
} while (p != u);
}
};
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
dfs(i, -1, dfs);
}
}
//缩点+建图
for (int i = 1; i <= n; ++i) {
for (auto v: ve[i]) {
if (bel[i] != bel[v]) {
// add_edge(bel[i], bel[v])
}
}
}
点双连通分量
定义:不存在割点的极大双连通子图
性质:点双连通分量中任意两点都同时包含在至少一个简单环中
vector<vector<int> > ve(N), ans(N); //ans中存放每个点双,有bcc个
int dfn[N], low[N], bcc, top, idx, n;
int s[N]; //栈
inline void tarjan(int u, int fa) {
int son = 0;
low[u] = dfn[u] = ++idx;
s[++top] = u;
for (auto v: ve[u]) {
if(!dfn[v]) {
son++;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {
bcc++;
while(s[top + 1] != v) ans[bcc].push_back(s[top--]);//将子树出栈
ans[bcc].push_back(u);//把割点/树根也丢到点双里
}
} else if(v != fa) low[u] = min(low[u], dfn[v]);
}
if(fa == 0 && son == 0) ans[++bcc].push_back(u);//特判独立点
}
void work() {
for (int i = 1; i <= n; ++i) {
if (dfn[i]) continue;
top = 0;
tarjan(i, 0);
}
}KMP
//找出第一个匹配下标
int kmp(string text, string pattern) {
int n = text.size(), m = pattern.size();
if (m == 0) {
return 0;
}
vector<int> next(m);
for (int i = 1, j = 0; i < m; i++) {
while (j > 0 && pattern[i] != pattern[j]) {
j = next[j - 1];
}
if (pattern[i] == pattern[j]) {
j++;
}
next[i] = j;
}
for (int i = 0, j = 0; i < n; i++) {
while (j > 0 && text[i] != pattern[j]) {
j = next[j - 1];
}
if (text[i] == pattern[j]) {
j++;
}
if (j == m) {
return i - m + 1;
}
}
return -1;
}
int ne[N];
void get_Next(string s) //这个函数对字符串s进行预处理得到next数组
{
int j = 0;
ne[0] = 0; //初始化
for (int i = 1; i < s.size(); i++) { //i指针指向的是后缀末尾,j指针指向的是前缀末尾
while (j > 0 && s[i] != s[j]) j = ne[j - 1]; //前后缀不相同,去找j前一位的最长相等前后缀
if (s[i] == s[j]) j++; //前后缀相同,j指针后移
ne[i] = j; //更新next数组
}
}
int strSTR(string s, string t) //这个函数是从s中找到t,如果存在返回t出现的位置,如果不存在返回-1
{
if(t.size()==0) return 0;
get_Next(t);
int j = 0;
for(int i = 0; i < s.size(); i++){
while(j>0&&s[i]!= t[j]) j = ne[j-1];
if(s[i]==t[j]) j++;
if(j==t.size()) {
// 找到匹配后的处理
return i - t.size() + 1;
}
}
return -1;
}字符串哈希
const int N = 2e6 + 5; // 最大字符串的个数
const int M = 2e6 + 10; // 题目中字符串的最大长度
const ull base = 131; // 131,13331不容易哈希碰撞
// p[i]:表示p的i次方
// h[i]:表示s[1~i]的哈希值,如h[2]表示字符串s前两个字符组成字符串的哈希值
ull p[N], h[N];
//int n;
// 预处理hash函数的前缀和,时间复杂度O(n)
void init(string s) {
// 下标从1开始
int n = s.size() - 1;
// p^0=1,空串哈希值为0
p[0] = 1, h[0] = 0;
for (int i = 1; i <= n; i++) {
p[i] = p[i - 1] * base;
h[i] = h[i - 1] * base + s[i]; // 前缀和计算公式
}
}
// 计算s[l~r](子串)的hash值,时间复杂度O(1)
ull get(int l, int r) {
return h[r] - h[l - 1] * p[r - l + 1]; // 区间和计算字串的hash值
}
// 判断s中的两个子串是否相同
bool substr(int l1, int r1, int l2, int r2) {
return get(l1, r1) == get(l2, r2);
}
// 求ss的哈希值(下标从0开始)
ull gethash(string ss) {
ull ret = 0;
for (int i = 0; i < ss.size(); ++i)
ret = ret * base + (ull) ss[i];
return ret;
}ac自动机
最原始的问题情境就是“给定n个模式串和1个文本串,求有多少种模式串在文本串里出现过。”
同一个模式串视为一种
const int maxn = 2 * 1e6 + 9;
int trie[maxn][26]; //字典树
int cntword[maxn]; //记录该单词出现次数
int fail[maxn]; //失败时的回溯指针
int cnt = 0;
void insertWords(string s) {
int root = 0;
for (int i = 0; i < s.size(); i++) {
int next = s[i] - 'a';
if (!trie[root][next])
trie[root][next] = ++cnt;
root = trie[root][next];
}
cntword[root]++; //当前节点单词数+1
}
void getFail() {
queue<int> q;
for (int i = 0; i < 26; i++) { //将第二层所有出现了的字母扔进队列
if (trie[0][i]) {
fail[trie[0][i]] = 0;
q.push(trie[0][i]);
}
}
//fail[now] ->当前节点now的失败指针指向的地方
// tire[now][i] -> 下一个字母为i+'a'的节点的下标为tire[now][i]
while (!q.empty()) {
int now = q.front();
q.pop();
for (int i = 0; i < 26; i++) { //查询26个字母
if (trie[now][i]) {
//如果有这个子节点为字母i+'a',则
//让这个节点的失败指针指向(((他父亲节点)的失败指针所指向的那个节点)的下一个节点)
//有点绕,为了方便理解特意加了括号
fail[trie[now][i]] = trie[fail[now]][i];
q.push(trie[now][i]);
} else//否则就让当前节点的这个子节点
//指向当前节点fail指针的这个子节点
trie[now][i] = trie[fail[now]][i];
}
}
}
int query(string s) {
int now = 0, ans = 0;
for (int i = 0; i < s.size(); i++) { //遍历文本串
now = trie[now][s[i] - 'a']; //从s[i]点开始寻找
for (int j = now; j && cntword[j] != -1; j = fail[j]) {
//一直向下寻找,直到匹配失败(失败指针指向根或者当前节点已找过).
ans += cntword[j];
cntword[j] = -1; //将遍历国后的节点标记,防止重复计算
}
}
return ans;
}
void work() {
int n;
cin >> n;
string s;
for (int i = 0; i < n; ++i) {
cin >> s; // 模式串
insertWords(s);
}
getFail();
// 文本串
cin >> s;
cout << query(s) << '\n';
}
ACAM-dfs优化
统计每种模式串的数量、文本串每个位置匹配的最短后缀的模式串的长度
#include<bits/stdc++.h>
using namespace std;
//#define int long long
#define ull uint64_t
#define PII pair<int,int>
//#define int __int128
#define ll long long
//#define double long double
const int mod = 998244353, Mod = 1e9 + 7;
const int N = 2e5 + 5, M = (1 << 22) + 5;
//const double PI = acos(-1.0);
const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
struct Node {
int son[26];
int fail = 0;
int len = 1e9;
//len记录当前状态的最短后缀长度,即有abc、bc、c的情况下,abc的最短后缀长度为1,即c
int idx = 0;//对模式串进行编号,相同模式串编号相同
int cnt = 0;//cnt记录模式串的个数
void init() {
for (int i = 0; i < 26; i++) son[i] = 0;
len = 1e9;
fail = 0;
cnt = 0;
idx = 0;
}
};
struct ACAM {
Node tr[N];
int tot;
int pidx; // 当前模式串编号
queue<int> q; // bfs求fail
vector<int> g[N]; // fail 树
ACAM() {
for (auto & i : tr) i.init();
tot = 0, pidx = 0;
}
void init() {
for (int i = 0; i <= tot; ++i) {
tr[i].init();
g[i].clear();
}
tot = 0, pidx = 0;
}
void insert(string& s, int &idx) {//idx记录当前模式串编号
int u = 0, len = s.size();
for (char i : s) {
int &son = tr[u].son[i - 'a'];
if (!son) son = ++tot;
u = son;
}
tr[u].len = len;
// 由于有可能出现相同的模式串,需要将相同的映射到同一个编号
if (!tr[u].idx) tr[u].idx = ++pidx; // 第一次出现,新增编号
idx = tr[u].idx; // 这个模式串的编号对应这个结点的编号
}
void build() {
for (int i = 0; i < 26; i++)
if (tr[0].son[i]) {
q.push(tr[0].son[i]);
g[0].push_back(tr[0].son[i]); // 不要忘记这里的 fail
}
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (tr[u].son[i]) {
tr[tr[u].son[i]].fail = tr[tr[u].fail].son[i];
g[tr[tr[u].fail].son[i]].push_back(tr[u].son[i]);
// 记录 fail 树, fail[u] -> u
q.push(tr[u].son[i]);
} else
tr[u].son[i] = tr[tr[u].fail].son[i];
}
}
// dfs(0);
}
/* ------------------统计匹配每种模式串的数量----------------------*/
//先query再dfs合并答案
void query(string &s) {
int u = 0;
for (int i = 0; i < s.size(); i++) {
u = tr[u].son[s[i] - 'a'];
tr[u].cnt ++;
}
}
//将叶子结点的答案合并给父结点, dfs(0)
void dfs(int u) {
for (int v: g[u]) {
dfs(v);
tr[u].cnt += tr[v].cnt;
}
// ans[tr[u].idx] += tr[u].cnt; // 对模式串编号idx记录答案
}
/* ------------------统计匹配每种模式串的数量----------------------*/
/*-----------------最短后缀-----------------------*/
//build()后dfs,再query
//求最短后缀的长度, dfs1(0)
void dfs1(int u) {
//更新子树的最小后缀长度
for (int v: g[u]) {
tr[v].len = min(tr[v].len, tr[u].len);
dfs(v);
}
}
void query1(string &s) {
int u = 0;
for (int i = 0; i < s.size(); ++i) {
u = tr[u].son[s[i] - 'a'];
int len = tr[u].len;//匹配出的s[i]结尾的最短后缀长度
}
}
/*-----------------最短后缀-----------------------*/
};Pollard Rho
求出x的所有质因子O(n^(1/4))
using f64 = long double;
int p;
f64 invp;
void setmod(int x){
p = x,invp = (f64)1 / x;
}
int mul(int a,int b){
int z = a * invp * b + 0.5;
int res = a * b - z * p;
return res + (res >> 63 & p);
}
int pow(int a,int x,int res = 1){
for (;x;x >>= 1, a = mul(a,a))
if (x & 1) res = mul(res,a);
return res;
}
bool checkprime(int p){
if (p == 1) return 0;
setmod(p);
int d = __builtin_ctzll(p - 1),s = (p - 1) >> d;
for (int a : {2, 3, 5, 7, 11, 13, 82, 373}){
if (a % p == 0)
continue;
int x = pow(a,s),y;
for (int i = 0;i < d;++i,x = y){
y = mul(x,x);
if (y == 1 && x != 1 && x != p - 1){
return false;
}
}
if (x != 1) return false;
}
return 1;
}
int rho(int n){
if (!(n & 1)) return 2;
static std::mt19937_64 gen((size_t)"hehezhou");
int x = 0,y = 0,prod = 1;
auto f = [&](int o){return mul(o,o) + 1;};
setmod(n);
for (int t = 30,z = 0;t % 64 || gcd(prod,n) == 1;++t){
if (x == y) x = ++z,y = f(x);
if (int q = mul(prod,x + n - y)) prod = q;
x = f(x),y = f(f(y));
}
return gcd(prod,n);
}
vector<int> factor(int x){
vector<int> res;
auto f = [&](auto f,int x){
if (x == 1) return;
if (checkprime(x)) return res.push_back(x);
int y = rho(x);
f(f,y),f(f,x / y);
};
f(f,x),sort(res.begin(),res.end());
return res;
}
void work() {
int x;
// 求出x的所有质因子O(n^(1/4))
vector<int> ans = factor(x);
}
莫队
普通莫队
排序:
void add(int i) {
sum += num[a[i]];
num[a[i]] ++;
}
void del(int i) {
num[a[i]] --;
sum -= num[a[i]];
}
{
//排序
int block = ::sqrt(n);
std::sort(Q.begin(), Q.end(), [&](E a, E b) {
if (a.l / block != b.l / block) return a.l < b.l;
return (a.l / block) & 1 ? a.r > b.r : a.r < b.r;
});
//移动到每个[l,r]
int l = 1, r = 0;
for (int i = 0; i < q; ++i) {
while (l < Q[i].l) del(l++);
while (l > Q[i].l) add(--l);
while (r < Q[i].r) add(++r);
while (r > Q[i].r) del(r--);
ans[Q[i].id] = sum;
}
}SOS DP
SOS DP,全称 Sum over Subsets dynamic programming,意为子集和 DP,用来解决一些涉及子集和计算的问题。

//求j的子集
for (int i = 0; i < N; ++i) {
for (int j = 0; j < 1 << N; ++j) {
if (j >> i & 1) f[j] += f[j ^ (1 << i)];
}
}
//求j的超集
for (int i = 0; i < N; ++i) {
for (int j = 0; j < 1 << N; ++j) {
if (j >> i & 1) f[j] += f[!(j ^ (1 << i))];
}
}O(3m)枚举每个集合的子集
for (int i = 0; i < 1 << m; ++i) {
for (int j = i; j; --j &= i) {
//j和j^i为i的子集
}
}笛卡尔树

笛卡尔树是形如上图的一棵树,满足:
- 堆的性质。如上图的小根堆,两子树的值都大于等于父亲的值
- 二叉搜索树的性质。左子树节点的下标都小于根的下标,右子树节点的下标都大于根的下标,显然按中序遍历这棵树可以得到原序列
- 询问原序列中i到j(i<j)最小值可以通过找到i到j的lca,即为最小值
线性构造笛卡尔树(小根堆)
//fa为父亲节点,ls为左儿子,rs为右儿子
int n, v[N], fa[N], ls[N], rs[N];
//s为栈,top为栈顶
int s[N], top;
void init_tree() {
for (int i = 1; i <= n; ++i) ls[i] = rs[i] = fa[i] = 0;
top = 0;
}
void Tree() {
// 以下标i作为节点
// for (int i = 1; i <= n; i++) {
// cin >> v[i];
// while (top && v[s[top]] > v[i])
// ls[i] = s[top], top--;
// fa[i] = s[top];
// fa[ls[i]] = i;
// if (fa[i]) rs[fa[i]] = i;
// s[++top] = i;
// }
// 以值v[i]作为节点
for (int i = 1; i <= n; i++) {
cin >> v[i];
while (top && s[top] > v[i])
ls[v[i]] = s[top], top--;
fa[v[i]] = s[top];
fa[ls[v[i]]] = v[i];
if (fa[v[i]]) rs[fa[v[i]]] = v[i];
s[++top] = v[i];
}
}最小表示法
O(n)求出一个序列循环同构中最小的那一个(在字符串中表示为字典序最小的一个循环同构)
auto get_min = [](const int ve[]) { //下标从0开始,0~n-1
int k = 0, i = 0, j = 1;
while (k < n && i < n && j < n) {
if (ve[(i + k) % n] == ve[(j + k) % n]) k++;
else {
if (ve[(i + k) % n] > ve[(j + k) % n]) i += k + 1;
else j += k + 1;
if (i == j) ++i;
k = 0;
}
}
int op = min(i, j); //op表示最小表示的起点
return op;
// for (i = 0; i < n; ++i)
// cout << ve[(op + i) % n] << " \n"[i == n - 1];
};数位dp模版
int f[N], a[20];
//统计前导0
int dfs(int pos, int lim) {//当前枚举到第pos位,lim表示当前是否到数的上限
if (pos < 1) {
//搜索结束,返回答案
return 1;
}
if (!lim && f[pos] != -1) return f[pos];//记忆化搜索
int up = lim ? a[pos] : 9;
int res = 0;
for (int i = 0; i <= up; ++i) {
res += dfs(pos - 1, lim && i == a[pos]);
}
if (!lim) f[pos] = res;
return res;
}
//不统计前导0
int dfs1(int pos, int lim, int lead) {//当前枚举到第pos位,lim表示当前是否到数的上限
if (pos < 1) {
//搜索结束,返回答案
if (lead) {
//当前数为0
}
return 1;
}
if (!lim && !lead && f[pos] != -1) return f[pos];//记忆化搜索
int up = lim ? a[pos] : 9;
int res = 0;
for (int i = 0; i <= up; ++i) {
res += dfs1(pos - 1, lim && i == a[pos], lead && i == 0);
}
if (!lim && !lead) f[pos] = res;
return res;
}
int cal(int x) {
if (x <= 0) return 0;
int len = 0;
while (x) {
a[++len] = x % 10;
x /= 10;
}
return dfs(len, 1);
}
void solve() {
int l, r;
cin >> l >> r;
int ans = cal(r) - cal(l - 1);
cout << ans;
}
__builtin函数
1. __builtin_ctz()/__builtin_ctzll()
返回二进制末尾0的个数
2. __builtin_clz()/__builtin_clzll()
返回二进制前导0的个数
3. __builtin_popcount()/__builtin_popcountll()
返回二进制中1的个数
4. __builtin_parity()/__builtin_parityll()
返回二进制中1的个数的奇偶
5. __builtin_ffs()/__builtin_ffsll()
返回二进制最后一个1在第几位
比如:8=1000,返回4
6.__builtin_sqrt()
快速开平方,比sqrt快接近10陪





 浙公网安备 33010602011771号
浙公网安备 33010602011771号